遗传算法（GA）的实现（基于实数编码，Python附源码）

遗传算法的算法步骤以及基于二进制编码的遗传算法实现参考：
遗传算法（GA）的实现（基于二进制编码，Python）

基于实数编码方式的遗传算法的实现

待求解问题：

求最大值，取值范围：x∈[-50,50]。
1、库的导入

import numpy as np
import random
import matplotlib.pyplot as plt

2、目标函数
待求解问题即为目标函数，同时作为适应度函数。

def function(x):
    y = 0
    for i in range(len(x)):
        y = y + (x[i]**2 - 10 * np.cos(2 * np.pi * x[i]) + 10 )
    return y

3、选择函数
使用轮盘赌选择法，分别计算出每个个体的选择概率和累计概率，生成种群数量个0-1之间随机数，将每个随机数依次与个体的累计概率作比较，若大于第i个个体的累计概率，小于第i+1个个体的累计概率，则第i+1个个体被选择进入下一代。

#选择函数，三个参数：种群个体、种群数量、适应度值
def select(population,population_size,fitness):
    #fitness_proportion用来保存每个个体的选择概率
    fitness_proportion = []
    #计算适应度之和
    fitness_sum = 0
    for i in range(population_size):
        fitness_sum += fitness[i]   
    #计算每个个体的选择概率
    for i in range(population_size):
        fitness_proportion.append(fitness[i] / fitness_sum)
    #pie_fitness保存每个个体的累计概率
    pie_fitness = []
    cumsum = 0.0
    for i in range(population_size):
        pie_fitness.append(cumsum + fitness_proportion[i])  #pie_fitness为由1到i个个体相加的适应度和组成的list
        cumsum += fitness_proportion[i]  #所有个体生存率之和
    # 生成随机数在轮盘上选点[0, 1)
    random_selection = []
    for i in range(population_size):
        random_selection.append(random.random())   #返回随机生成的一个实数，它在[0,1)范围内。
    # 选择新种群
    new_population = []
    random_selection_id = 0
    while random_selection_id < population_size:
        #随机数处于个体对应的累计区间时，则将这个个体赋给新种群
        for i in range(population_size):
            if random_selection[random_selection_id] < pie_fitness[i]:
                new_population.append(population[i])
                break
        random_selection_id += 1
    population = new_population
    return population

4、交叉函数
每两个个体为一组，针对每组个体，随机生成0-1之间的随机数，与交叉概率比较，若小于交叉概率，则随机生成个体数组长度内的数值作为交换点，然后在该交换点对两个个体的基因片段进行交换（例如个体是由20个数组成的数组，长度为20，则随机生成0到20间的整数作为交行点），完成交换后，新的一组个体取代原先的一组个体。

#交叉函数，四个参数：种群个体、种群数量、交叉概率、维度信息
def crosscover(population,population_size,pc,dimen):
    for i in range(0, population_size - 1, 2):  #每两个一对
        #如果生成的随机数小于交叉概率
        if random.random() < pc:
            # 随机选择交叉点,random.randint(0, dimen-1),返回[0,dimen-1]之间的整数
            change_point = random.randint(0, dimen-1)
            temp1 = []
            temp2 = []
            #两个个体在交叉点进行交换
            temp1.extend(population[i][0: change_point])
            temp1.extend(population[i + 1][change_point:])
            temp2.extend(population[i + 1][0: change_point])
            temp2.extend(population[i][change_point:])
            population[i] = temp1
            population[i + 1] = temp2
    population = np.array(population)
    return population

5、变异函数
针对种群中的每个个体，随机生成0-1之间的随机数，与变异概率比较，若小于变异概率，则对该基因进行变异，变异过程中首先随机生成需要变异的个体基因数量，然后随机对这么多数量的基因重新生成取值范围的数替代该基因原数值（例如需要变异的个体基因数量为5，则随机对个体中的5个基因按照取值范围进行重新取值）。

#变异函数，四个参数：种群个体、种群数量、变异概率、维度信息
def mutation(population,population_size,pm,dimen):
    for i in range(population_size):
        #如果随机生成的数小于变异概率
        if random.random() < pm:
            #随机生成个体中需要进行变异的数的数量mutation_num
            mutation_num = random.randint(0, dimen-1)
            #随机选择个体中mutation_num个数进行重新赋值
            for j in range(mutation_num):
                mutation_point = random.randint(0, dimen-1)
                population[i][mutation_point] = np.random.uniform(low=-50, high=50)
    population = np.array(population)
    return population

6、算法主流程
将交叉概率设为0.6、变异概率设为0.05，种群数量为50，按照求解问题的要求，x总共有20个，因此个体是由20个实数组成，用数组形式（pop）保存每个个体，数组形式（fitness）保存每个个体的适应度值。
在取值范围[-50,50]内随机初始化种群个体，之后计算其适应度值并获取最大适应度值（bestfit）及对应的个体（bestpop）。
使用数组bestfitness保存每次迭代过程中的最优适应度值，开始迭代过程，迭代次数为1000次。每次迭代过程中依次进行选择、交叉、变异操作，之后将每个个体的取值控制在[-50,50]之间，之后计算适应度值，然后将此次迭代中的最优适应度值与上次迭代中的最优适应度值进行比较，将更大的适应度值与对应的个体进行保存，最后将此时的种群作为下一次迭代时的初始种群。
每次迭代过程中输出当前迭代次数以及最优适应度值。
迭代结束后输出最优适应度值以及对应的个体取值。

#解的取值范围
rangepop=[-50,50]
#种群数量
pn = 50
#迭代次数
iterators = 1000
#交叉概率
pc = 0.6
#变异概率
pm = 0.05
#解的维度信息
dimen = 20
#种群，为数组形式
pop = np.zeros((pn,dimen))
#种群个体适应度值，为数组形式
fitness=np.zeros(pn)
#随机初始化种群
for j in range(pn):
    pop[j] = np.random.uniform(low=-50, high=50,size=(1, dimen))
    #计算适应度值
    fitness[j] = function(pop[j])
#获取当前最优解bestpop和最优适应度值bestfit
bestpop, bestfit = pop[fitness.argmax()].copy(), fitness.max()
#bestfitness保存每次迭代中的最优适应度值，为数组形式
bestfitness=np.zeros(iterators)
#开始迭代训练
for i in range(iterators):
    #选择操作
    parents = select(pop,pn,fitness)
    #交叉操作
    crossover1 = crosscover(parents,pn,pc,dimen)
    #变异操作
    pop = mutation(crossover1,pn,pm,dimen)
    #将上一次迭代的最优适应度值和新的适应度值比较，选择更大的适应度值作为新的最优适应度值，对应的个体作为当前最优解
    for j in range(pn):
        #确保个体取值在取值范围内[-50,50]内
        pop[pop < rangepop[0]] = rangepop[0]
        pop[pop > rangepop[1]] = rangepop[1]
        #计算新个体适应度值
        fitness[j] = function(pop[j])
        #比较最优适应度值
        if fitness[j] > bestfit:
            bestfit = fitness[j]
            bestpop = pop[j]
    bestfitness[i] = bestfit
    print("当前迭代次数:", i+1)
    print("最优适应度值是:", bestfitness[i])
print("迭代结束后:")
print("最优解是:", bestpop)
print("最优适应度值是:", bestfitness[-1])

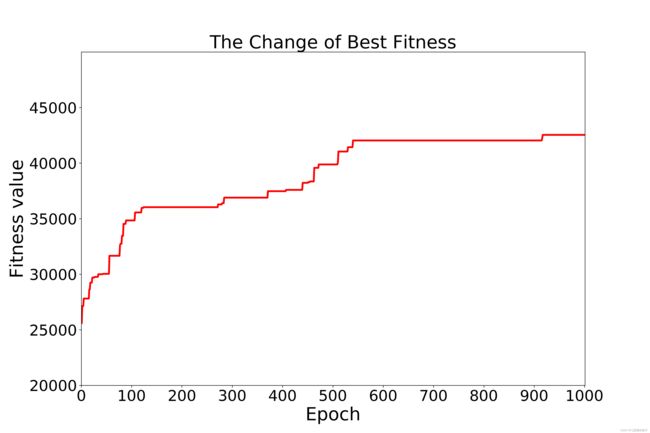
将best_fitness（每次迭代的最优适应度值）进行绘图并保存，可通过图片查看迭代过程中最优适应度值的变化情况。

fig=plt.figure(figsize=(15, 10), dpi=300)
plt.title('The Change of Best Fitness',fontdict={'weight':'normal','size': 30})
x=range(1,1001,1)
plt.plot(x,bestfitness,color="red",linewidth=3.0, linestyle="-")
plt.tick_params(labelsize=25)
plt.xlim(0,1001)
plt.ylim(20000,50000)
plt.xlabel("Epoch",fontdict={'weight':'normal','size': 30})
plt.ylabel("Fitness value",fontdict={'weight':'normal','size': 30})
plt.xticks(range(0,1001,100))
plt.yticks(range(20000,50000,5000))
plt.savefig("GA.png")
plt.show()

图中横轴为迭代次数，纵轴为最优适应度值。