c#编写高程拟合程序
高程拟合程序
- 1、功能简介
- 2、拟合原理
- 3、算法流程图
- 4、程序界面设计
- 5、程序运行
- 6、源代码
1、功能简介
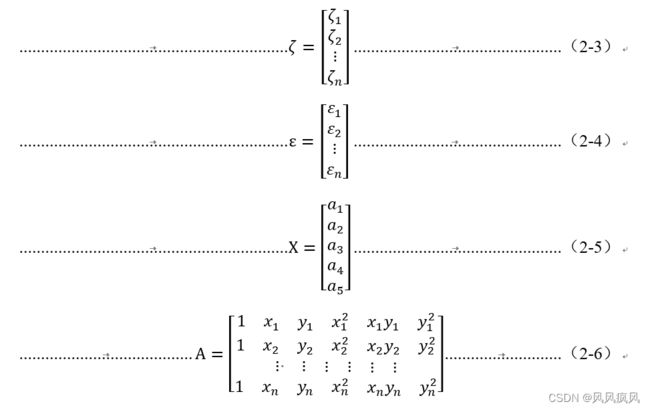
本程序主要用于解决高程拟合问题。本程序主要分为两个部分:高程拟合模型参数计算和根据计算出的模型计算高程异常。
高程拟合参数计算部分,本程序提供三种拟合方法,分别为二次曲面拟合、多项式平面拟合和四参数曲面拟合。可根据导入的已知点数据计算相应的拟合模型参数并计算内符合精度,还可在计算出参数后根据检验点数据计算外符合精度。数据导入采用TXT文件。内符合精度和外符合精度均精确到0.00001。拟合参数精确到小数点后六位。
高程异常计算部分,在计算完拟合参数后,导入坐标点数据,可计算高程异常并将结果导出为TXT文件。计算过程中长度单位均为米。高程异常值精确到0.1毫米。
2、拟合原理
3、算法流程图
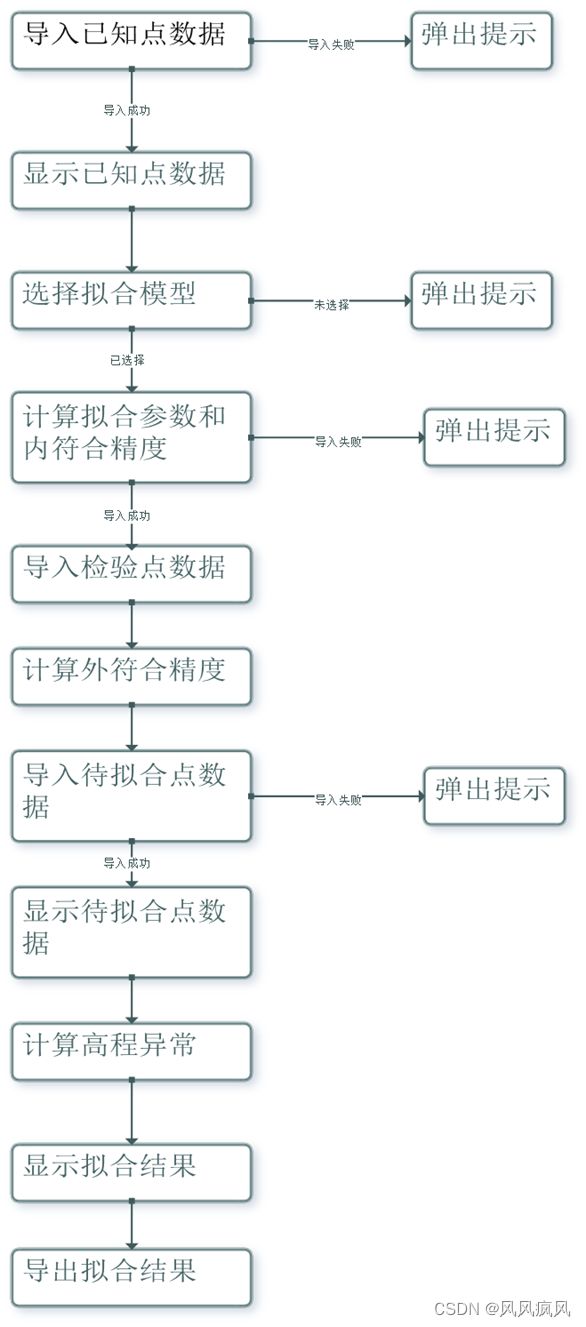
首先,导入已知点数据,显示已知点数据,选择拟合模型,计算拟合参数和内符合精度。然后导入检验点数据,计算外符合精度。计算完拟合参数后,可导入待拟合点,计算高程异常并导出结果。导入、导出均采用TXT文本文件,采用英文逗号分隔数据。在导入、导出时,如果出现错误,均会弹出提示。
4、程序界面设计
本程序界面设计主要分为两大部分:拟合参数计算和高程异常计算。使用tabControl控件实现两个部分的切换。界面样式使用IrisSkin4.dll插件进行美化。
拟合参数计算部分界面设计如下图:
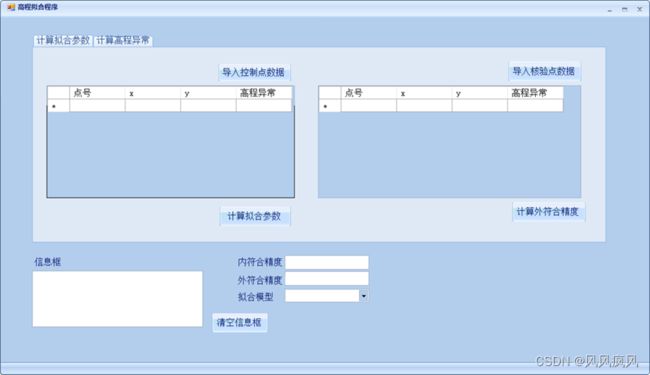
导入已知点数据、检验点数据、计算拟合参数、计算外符合精度使用Button按钮控制。导入的已知点数据、检验点数据格式均为“点号,x,y,高程异常”。内符合精度计算在计算拟合参数时同步进行,不需要单独操作。已知点数据和检验点数据采用dataGridView控件以表格形式显示。这两种点显示的数据均为点号、x、y和高程异常值。拟合模型选择使用comboBox控件进行选择操作。内、外符合精度使用textBox控件显示。界面下方有一个使用richTextBox空间组成的信息框,主要用来显示计算出来的拟合参数。
高程异常计算部分如下图:
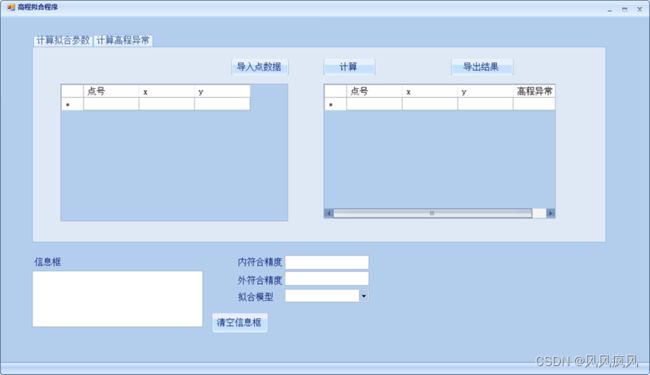
导入点数据、计算、导出结果操作使用Button按钮控制。待拟合点、拟合结果使用dataGridView控件以表格形式显示。待拟合点部分显示的数据包括点号、x、y。计算结果显示数据包括点号、x、y、高程异常。导入的待拟合点数据格式为“点号,x,y”,导出的结果数据格式均为“点号,x,y,高程异常”。
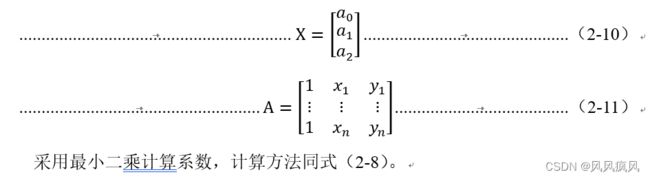
由三个拟合模型的拟合公式可以看出,二次曲面拟合至少需要7个已知点的数据参与拟合参数计算,多项式平面拟合至少需要4个已知点参与拟合参数计算,四参数曲面拟合至少需要5个已知点参与拟合参数计算。可根据已知点数量选择相应的拟合模型。
5、程序运行
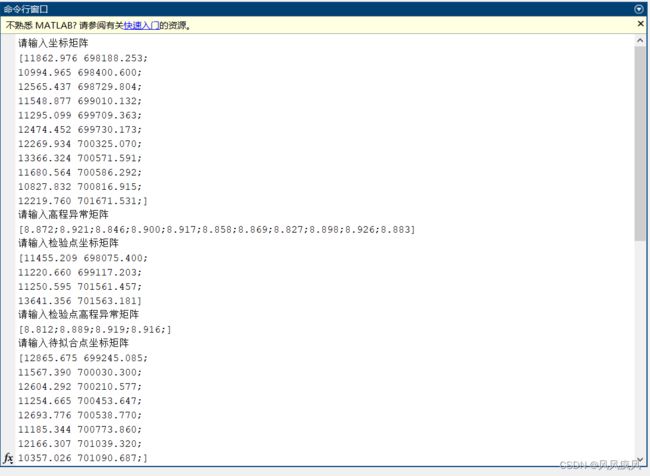
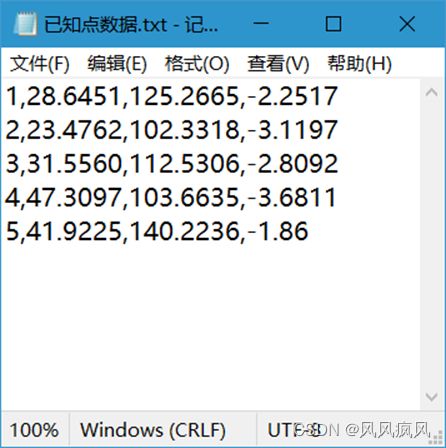
点击“导入已知点数据”,选择已知点数据文件,即可导入已知点数据。已知点数据采用txt文件存储,一行代表一个点数据,每一行格式为“点号,X,Y,高程异常值”,数据间用英文逗号相隔,数据单位均为米,下同。已知点示例数据如下图:
导入成功后,会在左侧表格显示数据,如果导入失败,会弹出提示并停止导入,已知点示例数据导入效果见下图:
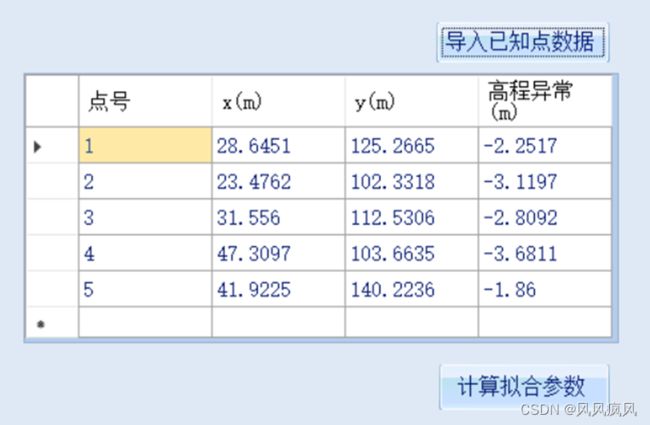
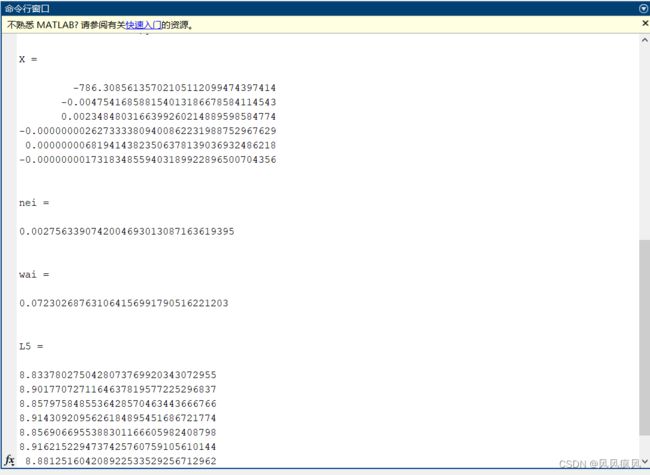
点击“计算拟合参数”按钮,即可自动根据选择的拟合模型计算相应的拟合参数,同时会计算拟合的内符合精度。拟合参数计算结果会在“信息框”部分显示,内符合精度会在“内符合精度”标签旁的文本框中显示,如下图:

点击“导入检验点数据”,选择检验点数据文件,即可导入检验点数据,如果导入失败,会弹出提示并停止导入。检验点数据采用txt文件存储,其格式与已知点数据一致。检验点数量无限制。检验点示例数据如下图:
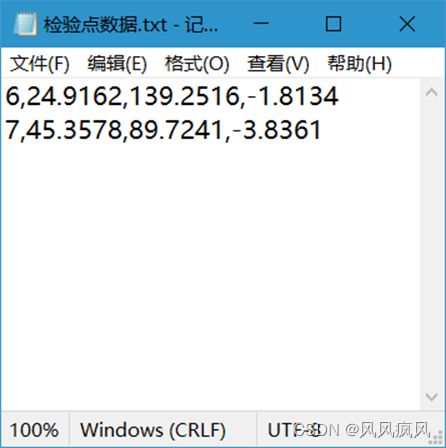
检验点示例数据导入效果如下图:
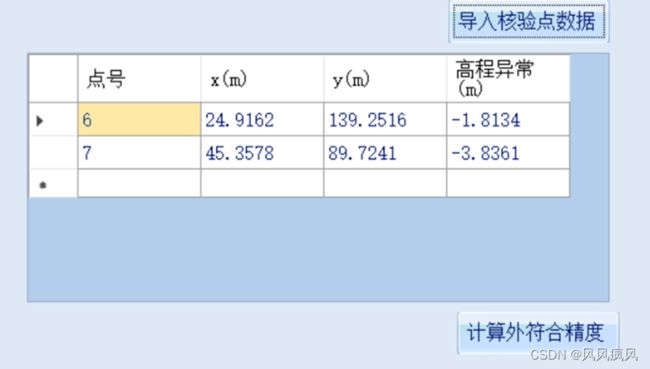
导入成功后,点击“计算外符合精度”按钮,即可计算外符合精度,外符合精度计算结果会显示在“外符合精度”标签旁的文本框中,如下图:

检验点数据只为用于计算外符合精度,不影响后续高程异常值的计算。如果没有检验点数据,可跳过该阶段,在计算出拟合参数后直接进行高程异常值的计算。
点击顶层导航栏的“计算高程异常”按钮,会跳转到计算高程异常的模块,其视图如下图:
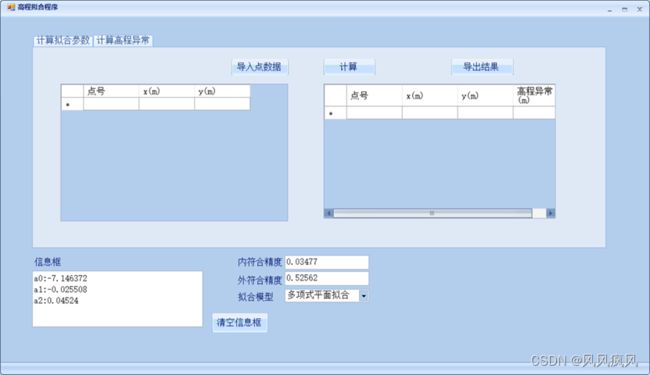
点击“导入点数据”按钮,选择待拟合点数据文件,即可导入待拟合点数据,如果导入失败,会弹出提示并停止导入。待拟合点数据采用txt文本格式存储,一行存储一个点数据,每一行的数据格式为“点号,X,Y”,数据单位均为米。待拟合点示例数据如下图:
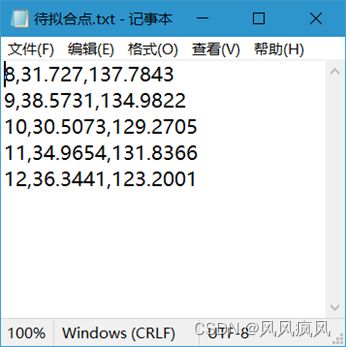
导入成功后会在左侧表格中显示待拟合点数据,待拟合示例数据导入效果见下图:
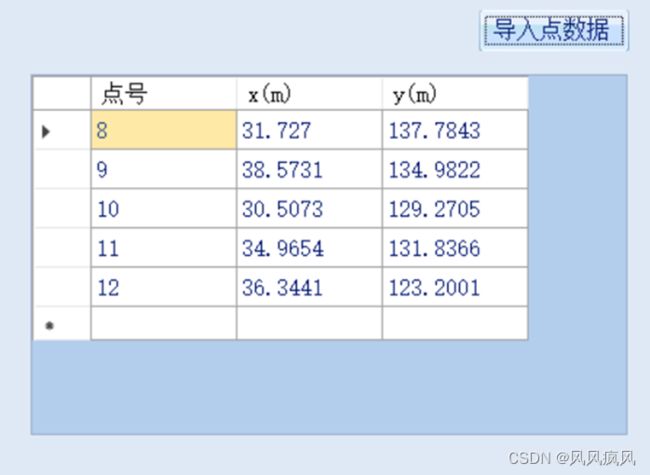
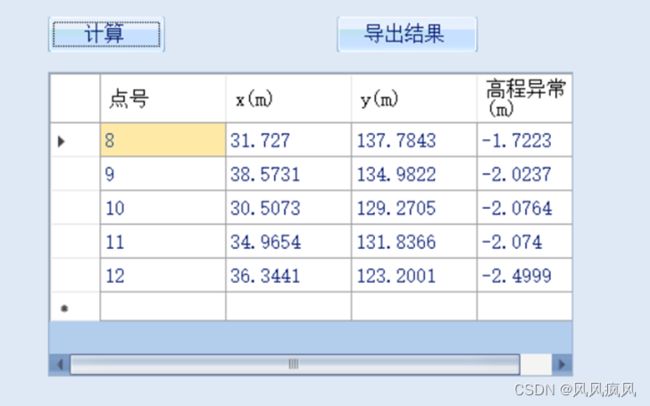
点击“计算”按钮,即可完成高程异常值的计算,计算结果回显示在右侧表格中,待拟合点示例数据计算结果显示效果如下图:
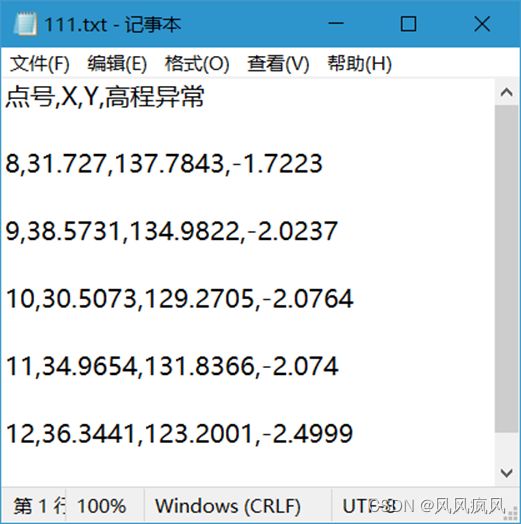
点击“导出结果”按钮,在弹出的文件框设置好文件名,即可将计算结果导出为txt文件,文件中每一行代表一个点数据,每一行的数据格式为“点号,X,Y,高程异常值”。导出的示例数据计算结果如下图:
6、源代码
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using System.IO;
namespace 高程拟合
{
public partial class Form1 : Form
{
public Form1()
{
this.skinEngine1 = new Sunisoft.IrisSkin.SkinEngine(((System.ComponentModel.Component)(this)));
this.skinEngine1.SkinFile = Application.StartupPath + @"\skins\office2007.ssk";
Sunisoft.IrisSkin.SkinEngine se = null;
se = new Sunisoft.IrisSkin.SkinEngine();
InitializeComponent();
}
public double miu;//内符合精度
public double M;//外符合精度;
List<KDG> kdg = new List<KDG>();//用于储存各种坐标的List表
List<DG> dg = new List<DG>();//转换后数据
List<ZG> zg = new List<ZG>();//转换结果
List<ZG> zg2 = new List<ZG>();//核验点拟合值
List<HYD> hy = new List<HYD>();//存储核验点
List<zhongjian> hzg = new List<zhongjian>();//核验点高程异常
List<zhongjian> hzg2 = new List<zhongjian>();//核验点拟合值高程异常
// List zhg = new List();
double[] yzc = new double[1000];//存储已知点拟合值和已知高程高程异常的差
double[] V = new double[1000];//外围点残差
double a0, a1, a2, a3, a4, a5;//多项式系数
public string s;//标记拟合模型
public struct KDG//控制点数据
{
public string dianhao;
public double dgao;//GNSS高
public double x;
public double y;
public double zgao;//水准高
public double GCYC;//高程异常
}
public struct HYD//核验点数据
{
public string dianhao;
public double dgao;//GNSS高
public double x;
public double y;
public double zgao;//水准高
public double GCYC;//高程异常
}
public struct zhongjian//迭代过程中的高程和误差
{
public double x;
public double y;
public double zgao;
public double GCYC;//高程异常
public double wc;
}
public struct DG//待转换的GPS高
{
public string dianhao;
public double x;
public double y;
public double gao;
}
public struct ZG//转换后GPS高
{
public string dianhao;
public double x;
public double y;
public double GCYC;//高程异常
public double gao;
public double cancha;
}
//导入已知点数据
private void button1_Click(object sender, EventArgs e)
{
kdg.Clear();//清空数据
dg.Clear();
string[] temp;
//打开选择文件对话框
OpenFileDialog openFileDialog1 = new OpenFileDialog(); //动态初始化
//打开txt文件
openFileDialog1.Filter = "(*.txt)|*.*";
openFileDialog1.FileName = "";
if (openFileDialog1.ShowDialog() == DialogResult.OK)
{
//使用StreamReader类来读取文件
FileStream fs = new FileStream(openFileDialog1.FileName, FileMode.Open, FileAccess.Read);
//FileStream 类,为文件提供 Stream(数据流),既支持同步读写操作,也支持异步读写操作。
//FileMode.open:指定操作系统应打开现有文件
// FileAccess.Read:对文件进行读取
StreamReader sr = new StreamReader(fs, Encoding.Default);
//StreamReader 类用于从流中读取字符串。
// 从数据流中读取每一行,直到文件的最后一行
while (!sr.EndOfStream)
{
temp = sr.ReadLine().Split(new[] { ',' }, StringSplitOptions.RemoveEmptyEntries);
KDG kdg1 = new KDG();
kdg1.dianhao = temp[0];
kdg1.x = Convert.ToDouble ( temp[1]);
kdg1.y = Convert.ToDouble(temp[2]);
kdg1.GCYC = Convert.ToDouble(temp[3]);//高程异常值
kdg.Add(kdg1);
}
sr.Close();
}
else
{
MessageBox.Show("文件导入失败!");
}
GridBuild2();
}
public void GridBuild2()
{
for (int i = 0; i < kdg.Count(); i++)
{
dataGridView1.Rows.Add();
dataGridView1.Rows[i].Cells[0].Value = kdg[i].dianhao;
dataGridView1.Rows[i].Cells[1].Value = kdg[i].x;
dataGridView1.Rows[i].Cells[2].Value = kdg[i].y;
dataGridView1.Rows[i].Cells[3].Value = kdg[i].GCYC; //高程异常
}
}
//计算高程拟合参数
private void button3_Click(object sender, EventArgs e)
{
int n = kdg.Count();
double[,] pL = new double[n, 1];
double wch = 0;//误差平方和
s = comboBox1.Text;
switch (s)
{
case"二次曲面拟合模型":
double[,] pA = new double[n, 6];
for (int i = 0; i < kdg.Count(); i++)//通过数组构造矩阵
{
pA[i, 0] = 1;
pA[i, 1] = kdg[i].x;
pA[i, 2] = kdg[i].y;
pA[i, 3] = kdg[i].x*kdg[i].x;
pA[i, 4] = kdg[i].x * kdg[i].y;
pA[i, 5] = kdg[i].y * kdg[i].y;
pL[i, 0] = kdg[i].GCYC;
}
Matrix A1 = new Matrix(pA);//运用最小二乘计算
Matrix L1 = new Matrix(pL);
Matrix Nbb = A1.Transpose() * A1;
Nbb.InvertGaussJordan();
Matrix X = Nbb * A1.Transpose() * L1;
a0 = Math.Round( X[0, 0],6);//模型参数
a1 = Math.Round( X[1, 0],6);
a2 =Math.Round( X[2, 0],6);
a3 =Math.Round( X[3, 0],6);
a4 = Math.Round( X[4, 0],6);
a5 =Math.Round(X[5, 0],6);
/* double[,] X110 = JMatrix.Multiply(JMatrix.Transpose(pA), pA);
double[,] X220 = JMatrix.Multiply(JMatrix.Transpose(pA), pL);
double[,] X330 = JMatrix.Multiply(JMatrix.Inverse(X110), X220);
a0 = X330[0, 0];
a1 = X330[1, 0];
a2 = X330[2, 0];
a3 = X330[3, 0];
a4 = X330[4, 0];
a5 = X330[5, 0];*/
//计算内符合精度miu
for (int i = 0; i < kdg.Count(); i++)
{
zhongjian ZJ = new zhongjian();
ZJ.x = kdg[i].x;
ZJ.y = kdg[i].y;
ZJ.GCYC = (a0 + a1 * kdg[i].x + a2 * kdg[i].y + a3 * kdg[i].x * kdg[i].x + a4 * kdg[i].x * kdg[i].y + a5 * kdg[i].y * kdg[i].y);
ZJ.wc = ZJ.GCYC - kdg[i].GCYC;
yzc[i] = ZJ.wc;
wch += ZJ.wc * ZJ.wc;
}
miu = Math.Sqrt(wch / (kdg.Count() - 1));
richTextBox1.Text += "a0:" + a0 + "\r\n" + "a1:" + a1 + "\r\n" + "a2:" + a2 + "\r\n" + "a3:" + a3 + "\r\n" + "a4:" + a4 + "\r\n" + "a5:" + a5 + "\r\n";//显示参数计算结果
textBox1.Text = Convert.ToString(Math.Round(miu,5));
break;
case"多项式平面拟合模型":
double[,] pA2 = new double[n, 3];
for (int i = 0; i < kdg.Count(); i++)
{
pA2[i, 0] = 1;
pA2[i, 1] = kdg[i].x;
pA2[i, 2] = kdg[i].y;
pL[i, 0] = kdg[i].GCYC;
}
Matrix A2 = new Matrix(pA2);//构造矩阵
Matrix L2 = new Matrix(pL);
Matrix Nbb2 = A2.Transpose() * A2;
Nbb2.InvertGaussJordan();
Matrix X2 = Nbb2 * A2.Transpose() * L2;//最小二乘计算
a0 = Math.Round( X2[0, 0],6);//模型参数
a1 = Math.Round( X2[1, 0],6);
a2 =Math.Round( X2[2, 0],6);
//计算内符合精度miu
for (int i = 0; i < kdg.Count(); i++)
{
zhongjian ZJ = new zhongjian();
ZJ.x = kdg[i].x;
ZJ.y = kdg[i].y;
ZJ.GCYC = a0 + a1 * kdg[i].x + a2 * kdg[i].y;
ZJ.wc = ZJ.GCYC - kdg[i].GCYC;
yzc[i] = ZJ.wc;
wch += ZJ.wc * ZJ.wc;
}
miu = Math.Sqrt(wch / (kdg.Count() - 1));
richTextBox1.Text += "a0:" + a0 + "\r\n" + "a1:" + a1 + "\r\n" + "a2:" + a2 + "\r\n";
textBox1.Text = Convert.ToString(Math.Round(miu, 5));
break;
case"四参数曲面拟合模型":
double[,] pA3 = new double[n, 4];
for (int i = 0; i < kdg.Count(); i++)
{
pA3[i, 0] = 1;
pA3[i, 1] = kdg[i].x;
pA3[i, 2] = kdg[i].y;
pA3[i, 3] = kdg[i].x*kdg[i].y;
pL[i, 0] = kdg[i].GCYC;
}
Matrix A3 = new Matrix(pA3);;//构造矩阵
Matrix L3 = new Matrix(pL);
Matrix Nbb3 = A3.Transpose() * A3;
Nbb3.InvertGaussJordan();
Matrix X3 = Nbb3 * A3.Transpose() * L3;//最小二乘计算
a0 = Math.Round( X3[0, 0],6);//模型参数
a1 = Math.Round( X3[1, 0],6);
a2 =Math.Round( X3[2, 0],6);
a3 =Math.Round( X3[3, 0],6);
//计算内符合精度miu
for (int i = 0; i < kdg.Count(); i++)
{
zhongjian ZJ = new zhongjian();
ZJ.x = kdg[i].x;
ZJ.y = kdg[i].y;
ZJ.GCYC = a0 + a1 * kdg[i].x + a2 * kdg[i].y + a3 * kdg[i].x * kdg[i].y;
ZJ.wc = ZJ.GCYC - kdg[i].GCYC;
yzc[i] = ZJ.wc;
wch += ZJ.wc * ZJ.wc;
}
miu = Math.Sqrt(wch / (kdg.Count() - 1));//计算内符合精度miu
richTextBox1.Text += "a0:" + a0 + "\r\n" + "a1:" + a1 + "\r\n" + "a2:" + a2 + "\r\n" + "a3:" + a3;
textBox1.Text = Convert.ToString(Math.Round(miu, 5));
break;
case "":
MessageBox.Show("请选择拟合模型!");
break;
default:
break;
}
}
//导入待转换坐标
private void button4_Click(object sender, EventArgs e)
{
dg.Clear();
string[] temp;
//打开选择文件对话框
OpenFileDialog openFileDialog1 = new OpenFileDialog(); //动态初始化
//打开txt文件
openFileDialog1.Filter = "(*.txt)|*.*";
openFileDialog1.FileName = "";
if (openFileDialog1.ShowDialog() == DialogResult.OK)
{
//使用StreamReader类来读取文件
FileStream fs = new FileStream(openFileDialog1.FileName, FileMode.Open, FileAccess.Read);
//FileStream 类,为文件提供 Stream(数据流),既支持同步读写操作,也支持异步读写操作。
//FileMode.open:指定操作系统应打开现有文件
// FileAccess.Read:对文件进行读取
StreamReader sr = new StreamReader(fs, Encoding.Default);
//StreamReader 类用于从流中读取字符串。
// 从数据流中读取每一行,直到文件的最后一行
while (!sr.EndOfStream)
{
// temp = sr.ReadLine().Split(',',',');
temp = sr.ReadLine().Split(new[] { ',' }, StringSplitOptions.RemoveEmptyEntries);
DG dg1=new DG ();
dg1.dianhao=temp[0];
dg1.x=Convert.ToDouble (temp[1]);
dg1.y=Convert.ToDouble (temp[2]);
dg.Add(dg1);
}
sr.Close();
}
else
{
MessageBox.Show("文件导入失败!");
}
GridBuild3();
}
public void GridBuild3()//显示待转换坐标
{
for (int i = 0; i < dg.Count(); i++)
{
dataGridView3.Rows.Add();
dataGridView3.Rows[i].Cells[0].Value =dg[i].dianhao;
dataGridView3.Rows[i].Cells[1].Value = dg[i].x;
dataGridView3.Rows[i].Cells[2].Value = dg[i].y;
}
}
//计算高程异常
private void button5_Click(object sender, EventArgs e)
{
for (int i = 0; i < dg.Count(); i++)
{
//计算高程异常
ZG zg1 = new ZG();
zg1.x = dg[i].x;
zg1.y = dg[i].y;
zg1.dianhao = dg[i].dianhao;
switch (s)
{
case "二次曲面拟合模型":
zg1.GCYC =Math.Round( a0 + a1 * dg[i].x + a2 * dg[i].y + a3 * dg[i].x * dg[i].x + a4 * dg[i].x * dg[i].y + a5 * dg[i].y * dg[i].y,4);
break;
case "多项式平面拟合模型":
zg1.GCYC =Math.Round( a0 + a1 * dg[i].x + a2 * dg[i].y,4);
break;
case "四参数曲面拟合模型":
zg1.GCYC = Math.Round( a0 + a1 * dg[i].x + a2 * dg[i].y + a3 * dg[i].x * dg[i].y,4);
break;
default:
break;
}
zg.Add(zg1);
}
GridBuild4();
}
public void GridBuild4()//显示计算结果
{
for (int i = 0; i < zg.Count(); i++)
{
dataGridView4.Rows.Add();
dataGridView4.Rows[i].Cells[0].Value = zg[i].dianhao;
dataGridView4.Rows[i].Cells[1].Value = zg[i].x;
dataGridView4.Rows[i].Cells[2].Value = zg[i].y;
dataGridView4.Rows[i].Cells[3].Value = zg[i].GCYC;//高程异常
}
}
//导出转换结果
private void button6_Click(object sender, EventArgs e)
{
int i = 0;
SaveFileDialog dlg = new SaveFileDialog();
dlg.Filter = "文本文件(*.txt)|*.txt";
if (dlg.ShowDialog() == DialogResult.OK)
{
string path = dlg.FileName;
StreamWriter sw = new StreamWriter(path);
sw.WriteLine("点号,X,Y,高程异常" + "\r\n");
for (i = 0; i < zg.Count(); i++)
{
sw.WriteLine(zg[i].dianhao + "," + zg[i].x + "," + zg[i].y + "," + zg[i].GCYC+"\r\n");
}
sw.Close();
MessageBox.Show("保存路径:" + dlg.FileName + "\r\n" + "保存成功!");
}
else
{
MessageBox.Show("保存失败!");
}
}
//导入核验点数据
private void button2_Click(object sender, EventArgs e)
{
hy.Clear();
string[] temp;
//打开选择文件对话框
OpenFileDialog openFileDialog1 = new OpenFileDialog(); //动态初始化
//打开txt文件
openFileDialog1.Filter = "(*.txt)|*.*";
openFileDialog1.FileName = "";
if (openFileDialog1.ShowDialog() == DialogResult.OK)
{
//使用StreamReader类来读取文件
FileStream fs = new FileStream(openFileDialog1.FileName, FileMode.Open, FileAccess.Read);
//FileStream 类,为文件提供 Stream(数据流),既支持同步读写操作,也支持异步读写操作。
//FileMode.open:指定操作系统应打开现有文件
// FileAccess.Read:对文件进行读取
StreamReader sr = new StreamReader(fs, Encoding.Default);
//StreamReader 类用于从流中读取字符串。
// 从数据流中读取每一行,直到文件的最后一行
while (!sr.EndOfStream)
{
// temp = sr.ReadLine().Split(',',',');
temp = sr.ReadLine().Split(new[] { ',' }, StringSplitOptions.RemoveEmptyEntries);
HYD hy1 = new HYD();
hy1.dianhao = temp[0];
hy1.x = Convert.ToDouble(temp[1]);
hy1.y = Convert.ToDouble(temp[2]);
hy1.GCYC = Convert.ToDouble(temp[3]);
hy.Add(hy1);
}
sr.Close();
}
else
{
MessageBox.Show("文件导入失败!");
}
GridBuild5();
}
public void GridBuild5()
{
for (int i = 0; i < hy.Count(); i++)
{
dataGridView2.Rows.Add();
dataGridView2.Rows[i].Cells[0].Value = hy[i].dianhao;
dataGridView2.Rows[i].Cells[1].Value = hy[i].x;
dataGridView2.Rows[i].Cells[2].Value = hy[i].y;
dataGridView2.Rows[i].Cells[3].Value = hy[i].GCYC;
}
}
//计算外符合精度
private void button7_Click(object sender, EventArgs e)
{
double wch2=0;//拟合误差平方和
for (int i = 0; i < hy.Count(); i++)//计算核验点拟合值
{
zhongjian zj3 = new zhongjian();
zj3.x = hy[i].x;
zj3.y = hy[i].y;
switch(s)
{
case "二次曲面拟合模型":
zj3.GCYC = a0 + a1 * hy[i].x + a2 * hy[i].y + a3 * hy[i].x * hy[i].x + a4 * hy[i].x * hy[i].y + a5 * hy[i].y * hy[i].y;
break;
case"多项式平面拟合模型":
zj3.GCYC = a0 + a1 * hy[i].x + a2 * hy[i].y;
break;
case"四参数曲面拟合模型":
zj3.GCYC = a0 + a1 * hy[i].x + a2 * hy[i].y + a3 * hy[i].x * hy[i].y;
break;
default:
break;
}
zj3.wc = zj3.GCYC - hy[i].GCYC;
hzg2.Add(zj3);
wch2 += zj3.wc * zj3.wc;
}
M = Math.Sqrt(wch2 / (hy.Count() - 1));//计算外符合精度
textBox2.Text = Convert.ToString(Math.Round(M,5));
}
private void button8_Click(object sender, EventArgs e)//清空信息框
{
richTextBox1.Text = "";
}
}
}
由于c#没有自带的矩阵库,程序运算需要自行增加矩阵库用于矩阵计算,可自行在在CSDN搜索矩阵库,这里分享一下我常用的一个矩阵库。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace 高程拟合
{
class Matrix
{
private int numColumns = 0; // 矩阵列数
private int numRows = 0; // 矩阵行数
private double eps = 0.0; // 缺省精度
private double[] elements = null; // 矩阵数据缓冲区
// 属性: 矩阵列数
public int Columns
{
get
{
return numColumns;
}
}
//属性: 矩阵行数
public int Rows
{
get
{
return numRows;
}
}
/*
索引器: 访问矩阵元素
@param row - 元素的行
@param col - 元素的列
*/
public double this[int row, int col]
{
get
{
return elements[col + row * numColumns];
}
set
{
elements[col + row * numColumns] = value;
}
}
// 属性: Eps
public double Eps
{
get
{
return eps;
}
set
{
eps = value;
}
}
// 基本构造函数
public Matrix()
{
numColumns = 1;
numRows = 1;
Init(numRows, numColumns);
}
/*
指定行列构造函数
@param nRows - 指定的矩阵行数
@param nCols - 指定的矩阵列数
*/
public Matrix(int nRows, int nCols)
{
numRows = nRows;
numColumns = nCols;
Init(numRows, numColumns);
}
/*
指定值构造函数
@param value - 二维数组,存储矩阵各元素的值
*/
public Matrix(double[,] value)
{
numRows = value.GetLength(0);
numColumns = value.GetLength(1);
double[] data = new double[numRows * numColumns];
int k = 0;
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
{
data[k++] = value[i, j];
}
}
Init(numRows, numColumns);
SetData(data);
}
/*
指定值构造函数
@param nRows - 指定的矩阵行数
@param nCols - 指定的矩阵列数
@param value - 一维数组,长度为nRows*nCols,存储矩阵各元素的值
*/
public Matrix(int nRows, int nCols, double[] value)
{
numRows = nRows;
numColumns = nCols;
Init(numRows, numColumns);
SetData(value);
}
/*
方阵构造函数
@param nSize - 方阵行列数
*/
public Matrix(int nSize)
{
numRows = nSize;
numColumns = nSize;
Init(nSize, nSize);
}
/*
方阵构造函数
@param nSize - 方阵行列数
@param value - 一维数组,长度为nRows*nRows,存储方阵各元素的值
*/
public Matrix(int nSize, double[] value)
{
numRows = nSize;
numColumns = nSize;
Init(nSize, nSize);
SetData(value);
}
/*
拷贝构造函数
@param other - 源矩阵
*/
public Matrix(Matrix other)
{
numColumns = other.GetNumColumns();
numRows = other.GetNumRows();
Init(numRows, numColumns);
SetData(other.elements);
}
/**
初始化函数
@param nRows - 指定的矩阵行数
@param nCols - 指定的矩阵列数
@return bool, 成功返回true, 否则返回false
*/
public bool Init(int nRows, int nCols)
{
numRows = nRows;
numColumns = nCols;
int nSize = nCols * nRows;
if (nSize < 0)
return false;
// 分配内存
elements = new double[nSize];
return true;
}
/*
设置矩阵运算的精度
@param newEps - 新的精度值
*/
public void SetEps(double newEps)
{
eps = newEps;
}
/*
取矩阵的精度值
@return double型,矩阵的精度值
*/
public double GetEps()
{
return eps;
}
/*
重载 + 运算符
@return Matrix对象
*/
public static Matrix operator +(Matrix m1, Matrix m2)
{
return m1.Add(m2);
}
/*
重载 - 运算符
@return Matrix对象
*/
public static Matrix operator -(Matrix m1, Matrix m2)
{
return m1.Subtract(m2);
}
/*
重载 * 运算符
@return Matrix对象
*/
public static Matrix operator *(Matrix m1, Matrix m2)
{
return m1.Multiply(m2);
}
/*
重载 double[] 运算符
@return double[]对象
*/
public static implicit operator double[](Matrix m)
{
return m.elements;
}
/*
将方阵初始化为单位矩阵
@param nSize - 方阵行列数
@return bool 型,初始化是否成功
*/
public bool MakeUnitMatrix(int nSize)
{
if (!Init(nSize, nSize))
return false;
for (int i = 0; i < nSize; ++i)
for (int j = 0; j < nSize; ++j)
if (i == j)
SetElement(i, j, 1);
return true;
}
/*
将矩阵各元素的值转化为字符串, 元素之间的分隔符为",", 行与行之间有回车换行符
@return string 型,转换得到的字符串
*/
public override string ToString()
{
return ToString(",", true);
}
/*
将矩阵各元素的值转化为字符串
@param sDelim - 元素之间的分隔符
@param bLineBreak - 行与行之间是否有回车换行符
@return string 型,转换得到的字符串
*/
public string ToString(string sDelim, bool bLineBreak)
{
string s = "";
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
{
string ss = GetElement(i, j).ToString("F");
s += ss;
if (bLineBreak)
{
if (j != numColumns - 1)
s += sDelim;
}
else
{
if (i != numRows - 1 || j != numColumns - 1)
s += sDelim;
}
}
if (bLineBreak)
if (i != numRows - 1)
s += "\r\n";
}
return s;
}
/**
将矩阵指定行中各元素的值转化为字符串
@param nRow - 指定的矩阵行,nRow = 0表示第一行
@param sDelim - 元素之间的分隔符
@return string 型,转换得到的字符串
*/
public string ToStringRow(int nRow, string sDelim)
{
string s = "";
if (nRow >= numRows)
return s;
for (int j = 0; j < numColumns; ++j)
{
string ss = GetElement(nRow, j).ToString("F");
s += ss;
if (j != numColumns - 1)
s += sDelim;
}
return s;
}
/*
将矩阵指定列中各元素的值转化为字符串
@param nCol - 指定的矩阵行,nCol = 0表示第一列
@param sDelim - 元素之间的分隔符
@return string 型,转换得到的字符串
*/
public string ToStringCol(int nCol, string sDelim /*= " "*/)
{
string s = "";
if (nCol >= numColumns)
return s;
for (int i = 0; i < numRows; ++i)
{
string ss = GetElement(i, nCol).ToString("F");
s += ss;
if (i != numRows - 1)
s += sDelim;
}
return s;
}
/*
设置矩阵各元素的值
@param value - 一维数组,长度为numColumns*numRows,存储
矩阵各元素的值
*/
public void SetData(double[] value)
{
elements = (double[])value.Clone();
}
/*
设置指定元素的值
@param nRow - 元素的行
@param nCol - 元素的列
@param value - 指定元素的值
@return bool 型,说明设置是否成功
*/
public bool SetElement(int nRow, int nCol, double value)
{
if (nCol < 0 || nCol >= numColumns || nRow < 0 || nRow >= numRows)
return false; // array bounds error
elements[nCol + nRow * numColumns] = value;
return true;
}
/*
获取指定元素的值
@param nRow - 元素的行
@param nCol - 元素的列
@return double 型,指定元素的值
*/
public double GetElement(int nRow, int nCol)
{
return elements[nCol + nRow * numColumns];
}
/**
获取矩阵的列数
@return int 型,矩阵的列数
*/
public int GetNumColumns()
{
return numColumns;
}
/**
* 获取矩阵的行数
* @return int 型,矩阵的行数
*/
public int GetNumRows()
{
return numRows;
}
/**
* 获取矩阵的数据
*
* @return double型数组,指向矩阵各元素的数据缓冲区
*/
public double[] GetData()
{
return elements;
}
/**
* 获取指定行的向量
*
* @param nRow - 向量所在的行
* @param pVector - 指向向量中各元素的缓冲区
* @return int 型,向量中元素的个数,即矩阵的列数
*/
public int GetRowVector(int nRow, double[] pVector)
{
for (int j = 0; j < numColumns; ++j)
pVector[j] = GetElement(nRow, j);
return numColumns;
}
/**
* 获取指定列的向量
*
* @param nCol - 向量所在的列
* @param pVector - 指向向量中各元素的缓冲区
* @return int 型,向量中元素的个数,即矩阵的行数
*/
public int GetColVector(int nCol, double[] pVector)
{
for (int i = 0; i < numRows; ++i)
pVector[i] = GetElement(i, nCol);
return numRows;
}
/**
* 给矩阵赋值
*
* @param other - 用于给矩阵赋值的源矩阵
* @return Matrix型,阵与other相等
*/
public Matrix SetValue(Matrix other)
{
if (other != this)
{
Init(other.GetNumRows(), other.GetNumColumns());
SetData(other.elements);
}
// finally return a reference to ourselves
return this;
}
/**
* 判断矩阵否相等
*
* @param other - 用于比较的矩阵
* @return bool 型,两个矩阵相等则为true,否则为false
*/
public override bool Equals(object other)
{
Matrix matrix = other as Matrix;
if (matrix == null)
return false;
// 首先检查行列数是否相等
if (numColumns != matrix.GetNumColumns() || numRows != matrix.GetNumRows())
return false;
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
{
if (Math.Abs(GetElement(i, j) - matrix.GetElement(i, j)) > eps)
return false;
}
}
return true;
}
/**
* 因为重写了Equals,因此必须重写GetHashCode
*
* @return int型,返回复数对象散列码
*/
public override int GetHashCode()
{
double sum = 0;
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
{
sum += Math.Abs(GetElement(i, j));
}
}
return (int)Math.Sqrt(sum);
}
/**
* 实现矩阵的加法
*
* @param other - 与指定矩阵相加的矩阵
* @return Matrix型,指定矩阵与other相加之和
* @如果矩阵的行/列数不匹配,则会抛出异常
*/
public Matrix Add(Matrix other)
{
// 首先检查行列数是否相等
if (numColumns != other.GetNumColumns() ||
numRows != other.GetNumRows())
throw new Exception("矩阵的行/列数不匹配。");
// 构造结果矩阵
Matrix result = new Matrix(this); // 拷贝构造
// 矩阵加法
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
result.SetElement(i, j, result.GetElement(i, j) + other.GetElement(i, j));
}
return result;
}
/**
* 实现矩阵的减法
*
* @param other - 与指定矩阵相减的矩阵
* @return Matrix型,指定矩阵与other相减之差
* @如果矩阵的行/列数不匹配,则会抛出异常
*/
public Matrix Subtract(Matrix other)
{
if (numColumns != other.GetNumColumns() ||
numRows != other.GetNumRows())
throw new Exception("矩阵的行/列数不匹配。");
// 构造结果矩阵
Matrix result = new Matrix(this); // 拷贝构造
// 进行减法操作
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
result.SetElement(i, j, result.GetElement(i, j) - other.GetElement(i, j));
}
return result;
}
/**
* 实现矩阵的数乘
*
* @param value - 与指定矩阵相乘的实数
* @return Matrix型,指定矩阵与value相乘之积
*/
public Matrix Multiply(double value)
{
// 构造目标矩阵
Matrix result = new Matrix(this); // copy ourselves
// 进行数乘
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
result.SetElement(i, j, result.GetElement(i, j) * value);
}
return result;
}
/**
* 实现矩阵的乘法
*
* @param other - 与指定矩阵相乘的矩阵
* @return Matrix型,指定矩阵与other相乘之积
* @如果矩阵的行/列数不匹配,则会抛出异常
*/
public Matrix Multiply(Matrix other)
{
// 首先检查行列数是否符合要求
if (numColumns != other.GetNumRows())
throw new Exception("矩阵的行/列数不匹配。");
// ruct the object we are going to return
Matrix result = new Matrix(numRows, other.GetNumColumns());
// 矩阵乘法,即
//
// [A][B][C] [G][H] [A*G + B*I + C*K][A*H + B*J + C*L]
// [D][E][F] * [I][J] = [D*G + E*I + F*K][D*H + E*J + F*L]
// [K][L]
//
double value;
for (int i = 0; i < result.GetNumRows(); ++i)
{
for (int j = 0; j < other.GetNumColumns(); ++j)
{
value = 0.0;
for (int k = 0; k < numColumns; ++k)
{
value += GetElement(i, k) * other.GetElement(k, j);
}
result.SetElement(i, j, value);
}
}
return result;
}
/**
* 复矩阵的乘法
*
* @param AR - 左边复矩阵的实部矩阵
* @param AI - 左边复矩阵的虚部矩阵
* @param BR - 右边复矩阵的实部矩阵
* @param BI - 右边复矩阵的虚部矩阵
* @param CR - 乘积复矩阵的实部矩阵
* @param CI - 乘积复矩阵的虚部矩阵
* @return bool型,复矩阵乘法是否成功
*/
public bool Multiply(Matrix AR, Matrix AI, Matrix BR, Matrix BI, Matrix CR, Matrix CI)
{
// 首先检查行列数是否符合要求
if (AR.GetNumColumns() != AI.GetNumColumns() ||
AR.GetNumRows() != AI.GetNumRows() ||
BR.GetNumColumns() != BI.GetNumColumns() ||
BR.GetNumRows() != BI.GetNumRows() ||
AR.GetNumColumns() != BR.GetNumRows())
return false;
// 构造乘积矩阵实部矩阵和虚部矩阵
Matrix mtxCR = new Matrix(AR.GetNumRows(), BR.GetNumColumns());
Matrix mtxCI = new Matrix(AR.GetNumRows(), BR.GetNumColumns());
// 复矩阵相乘
for (int i = 0; i < AR.GetNumRows(); ++i)
{
for (int j = 0; j < BR.GetNumColumns(); ++j)
{
double vr = 0;
double vi = 0;
for (int k = 0; k < AR.GetNumColumns(); ++k)
{
double p = AR.GetElement(i, k) * BR.GetElement(k, j);
double q = AI.GetElement(i, k) * BI.GetElement(k, j);
double s = (AR.GetElement(i, k) + AI.GetElement(i, k)) * (BR.GetElement(k, j) + BI.GetElement(k, j));
vr += p - q;
vi += s - p - q;
}
mtxCR.SetElement(i, j, vr);
mtxCI.SetElement(i, j, vi);
}
}
CR = mtxCR;
CI = mtxCI;
return true;
}
/**
* 矩阵的转置
*
* @return Matrix型,指定矩阵转置矩阵
*/
public Matrix Transpose()
{
// 构造目标矩阵
Matrix Trans = new Matrix(numColumns, numRows);
// 转置各元素
for (int i = 0; i < numRows; ++i)
{
for (int j = 0; j < numColumns; ++j)
Trans.SetElement(j, i, GetElement(i, j));
}
return Trans;
}
/**
* 实矩阵求逆的全选主元高斯-约当法
*
* @return bool型,求逆是否成功
*/
public bool InvertGaussJordan()
{
int i, j, k, l, u, v;
double d = 0, p = 0;
// 分配内存
int[] pnRow = new int[numColumns];
int[] pnCol = new int[numColumns];
// 消元
for (k = 0; k <= numColumns - 1; k++)
{
d = 0.0;
for (i = k; i <= numColumns - 1; i++)
{
for (j = k; j <= numColumns - 1; j++)
{
l = i * numColumns + j; p = Math.Abs(elements[l]);
if (p > d)
{
d = p;
pnRow[k] = i;
pnCol[k] = j;
}
}
}
// 失败
if (d == 0.0)
{
return false;
}
if (pnRow[k] != k)
{
for (j = 0; j <= numColumns - 1; j++)
{
u = k * numColumns + j;
v = pnRow[k] * numColumns + j;
p = elements[u];
elements[u] = elements[v];
elements[v] = p;
}
}
if (pnCol[k] != k)
{
for (i = 0; i <= numColumns - 1; i++)
{
u = i * numColumns + k;
v = i * numColumns + pnCol[k];
p = elements[u];
elements[u] = elements[v];
elements[v] = p;
}
}
l = k * numColumns + k;
elements[l] = 1.0 / elements[l];
for (j = 0; j <= numColumns - 1; j++)
{
if (j != k)
{
u = k * numColumns + j;
elements[u] = elements[u] * elements[l];
}
}
for (i = 0; i <= numColumns - 1; i++)
{
if (i != k)
{
for (j = 0; j <= numColumns - 1; j++)
{
if (j != k)
{
u = i * numColumns + j;
elements[u] = elements[u] - elements[i * numColumns + k] * elements[k * numColumns + j];
}
}
}
}
for (i = 0; i <= numColumns - 1; i++)
{
if (i != k)
{
u = i * numColumns + k;
elements[u] = -elements[u] * elements[l];
}
}
}
// 调整恢复行列次序
for (k = numColumns - 1; k >= 0; k--)
{
if (pnCol[k] != k)
{
for (j = 0; j <= numColumns - 1; j++)
{
u = k * numColumns + j;
v = pnCol[k] * numColumns + j;
p = elements[u];
elements[u] = elements[v];
elements[v] = p;
}
}
if (pnRow[k] != k)
{
for (i = 0; i <= numColumns - 1; i++)
{
u = i * numColumns + k;
v = i * numColumns + pnRow[k];
p = elements[u];
elements[u] = elements[v];
elements[v] = p;
}
}
}
// 成功返回
return true;
}
/**
* 复矩阵求逆的全选主元高斯-约当法
*
* @param mtxImag - 复矩阵的虚部矩阵,当前矩阵为复矩阵的实部
* @return bool型,求逆是否成功
*/
public bool InvertGaussJordan(Matrix mtxImag)
{
int i, j, k, l, u, v, w;
double p, q, s, t, d, b;
// 分配内存
int[] pnRow = new int[numColumns];
int[] pnCol = new int[numColumns];
// 消元
for (k = 0; k <= numColumns - 1; k++)
{
d = 0.0;
for (i = k; i <= numColumns - 1; i++)
{
for (j = k; j <= numColumns - 1; j++)
{
u = i * numColumns + j;
p = elements[u] * elements[u] + mtxImag.elements[u] * mtxImag.elements[u];
if (p > d)
{
d = p;
pnRow[k] = i;
pnCol[k] = j;
}
}
}
// 失败
if (d == 0.0)
{
return false;
}
if (pnRow[k] != k)
{
for (j = 0; j <= numColumns - 1; j++)
{
u = k * numColumns + j;
v = pnRow[k] * numColumns + j;
t = elements[u];
elements[u] = elements[v];
elements[v] = t;
t = mtxImag.elements[u];
mtxImag.elements[u] = mtxImag.elements[v];
mtxImag.elements[v] = t;
}
}
if (pnCol[k] != k)
{
for (i = 0; i <= numColumns - 1; i++)
{
u = i * numColumns + k;
v = i * numColumns + pnCol[k];
t = elements[u];
elements[u] = elements[v];
elements[v] = t;
t = mtxImag.elements[u];
mtxImag.elements[u] = mtxImag.elements[v];
mtxImag.elements[v] = t;
}
}
l = k * numColumns + k;
elements[l] = elements[l] / d; mtxImag.elements[l] = -mtxImag.elements[l] / d;
for (j = 0; j <= numColumns - 1; j++)
{
if (j != k)
{
u = k * numColumns + j;
p = elements[u] * elements[l];
q = mtxImag.elements[u] * mtxImag.elements[l];
s = (elements[u] + mtxImag.elements[u]) * (elements[l] + mtxImag.elements[l]);
elements[u] = p - q;
mtxImag.elements[u] = s - p - q;
}
}
for (i = 0; i <= numColumns - 1; i++)
{
if (i != k)
{
v = i * numColumns + k;
for (j = 0; j <= numColumns - 1; j++)
{
if (j != k)
{
u = k * numColumns + j;
w = i * numColumns + j;
p = elements[u] * elements[v];
q = mtxImag.elements[u] * mtxImag.elements[v];
s = (elements[u] + mtxImag.elements[u]) * (elements[v] + mtxImag.elements[v]);
t = p - q;
b = s - p - q;
elements[w] = elements[w] - t;
mtxImag.elements[w] = mtxImag.elements[w] - b;
}
}
}
}
for (i = 0; i <= numColumns - 1; i++)
{
if (i != k)
{
u = i * numColumns + k;
p = elements[u] * elements[l];
q = mtxImag.elements[u] * mtxImag.elements[l];
s = (elements[u] + mtxImag.elements[u]) * (elements[l] + mtxImag.elements[l]);
elements[u] = q - p;
mtxImag.elements[u] = p + q - s;
}
}
}
// 调整恢复行列次序
for (k = numColumns - 1; k >= 0; k--)
{
if (pnCol[k] != k)
{
for (j = 0; j <= numColumns - 1; j++)
{
u = k * numColumns + j;
v = pnCol[k] * numColumns + j;
t = elements[u];
elements[u] = elements[v];
elements[v] = t;
t = mtxImag.elements[u];
mtxImag.elements[u] = mtxImag.elements[v];
mtxImag.elements[v] = t;
}
}
if (pnRow[k] != k)
{
for (i = 0; i <= numColumns - 1; i++)
{
u = i * numColumns + k;
v = i * numColumns + pnRow[k];
t = elements[u];
elements[u] = elements[v];
elements[v] = t;
t = mtxImag.elements[u];
mtxImag.elements[u] = mtxImag.elements[v];
mtxImag.elements[v] = t;
}
}
}
// 成功返回
return true;
}
/**
* 对称正定矩阵的求逆
*
* @return bool型,求逆是否成功
*/
public bool InvertSsgj()
{
int i, j, k, m;
double w, g;
// 临时内存
double[] pTmp = new double[numColumns];
// 逐列处理
for (k = 0; k <= numColumns - 1; k++)
{
w = elements[0];
if (w == 0.0)
{
return false;
}
m = numColumns - k - 1;
for (i = 1; i <= numColumns - 1; i++)
{
g = elements[i * numColumns];
pTmp[i] = g / w;
if (i <= m)
pTmp[i] = -pTmp[i];
for (j = 1; j <= i; j++)
elements[(i - 1) * numColumns + j - 1] = elements[i * numColumns + j] + g * pTmp[j];
}
elements[numColumns * numColumns - 1] = 1.0 / w;
for (i = 1; i <= numColumns - 1; i++)
elements[(numColumns - 1) * numColumns + i - 1] = pTmp[i];
}
// 行列调整
for (i = 0; i <= numColumns - 2; i++)
for (j = i + 1; j <= numColumns - 1; j++)
elements[i * numColumns + j] = elements[j * numColumns + i];
return true;
}
/**
* 托伯利兹矩阵求逆的埃兰特方法
*
* @return bool型,求逆是否成功
*/
public bool InvertTrench()
{
int i, j, k;
double a, s;
// 上三角元素
double[] t = new double[numColumns];
// 下三角元素
double[] tt = new double[numColumns];
// 上、下三角元素赋值
for (i = 0; i < numColumns; ++i)
{
t[i] = GetElement(0, i);
tt[i] = GetElement(i, 0);
}
// 临时缓冲区
double[] c = new double[numColumns];
double[] r = new double[numColumns];
double[] p = new double[numColumns];
// 非Toeplitz矩阵,返回
if (t[0] == 0.0)
{
return false;
}
a = t[0];
c[0] = tt[1] / t[0];
r[0] = t[1] / t[0];
for (k = 0; k <= numColumns - 3; k++)
{
s = 0.0;
for (j = 1; j <= k + 1; j++)
s = s + c[k + 1 - j] * tt[j];
s = (s - tt[k + 2]) / a;
for (i = 0; i <= k; i++)
p[i] = c[i] + s * r[k - i];
c[k + 1] = -s;
s = 0.0;
for (j = 1; j <= k + 1; j++)
s = s + r[k + 1 - j] * t[j];
s = (s - t[k + 2]) / a;
for (i = 0; i <= k; i++)
{
r[i] = r[i] + s * c[k - i];
c[k - i] = p[k - i];
}
r[k + 1] = -s;
a = 0.0;
for (j = 1; j <= k + 2; j++)
a = a + t[j] * c[j - 1];
a = t[0] - a;
// 求解失败
if (a == 0.0)
{
return false;
}
}
elements[0] = 1.0 / a;
for (i = 0; i <= numColumns - 2; i++)
{
k = i + 1;
j = (i + 1) * numColumns;
elements[k] = -r[i] / a;
elements[j] = -c[i] / a;
}
for (i = 0; i <= numColumns - 2; i++)
{
for (j = 0; j <= numColumns - 2; j++)
{
k = (i + 1) * numColumns + j + 1;
elements[k] = elements[i * numColumns + j] - c[i] * elements[j + 1];
elements[k] = elements[k] + c[numColumns - j - 2] * elements[numColumns - i - 1];
}
}
return true;
}
/**
* 求行列式值的全选主元高斯消去法
*
* @return double型,行列式的值
*/
public double ComputeDetGauss()
{
int i, j, k, nis = 0, js = 0, l, u, v;
double f, det, q, d;
// 初值
f = 1.0;
det = 1.0;
// 消元
for (k = 0; k <= numColumns - 2; k++)
{
q = 0.0;
for (i = k; i <= numColumns - 1; i++)
{
for (j = k; j <= numColumns - 1; j++)
{
l = i * numColumns + j;
d = Math.Abs(elements[l]);
if (d > q)
{
q = d;
nis = i;
js = j;
}
}
}
if (q == 0.0)
{
det = 0.0;
return (det);
}
if (nis != k)
{
f = -f;
for (j = k; j <= numColumns - 1; j++)
{
u = k * numColumns + j;
v = nis * numColumns + j;
d = elements[u];
elements[u] = elements[v];
elements[v] = d;
}
}
if (js != k)
{
f = -f;
for (i = k; i <= numColumns - 1; i++)
{
u = i * numColumns + js;
v = i * numColumns + k;
d = elements[u];
elements[u] = elements[v];
elements[v] = d;
}
}
l = k * numColumns + k;
det = det * elements[l];
for (i = k + 1; i <= numColumns - 1; i++)
{
d = elements[i * numColumns + k] / elements[l];
for (j = k + 1; j <= numColumns - 1; j++)
{
u = i * numColumns + j;
elements[u] = elements[u] - d * elements[k * numColumns + j];
}
}
}
// 求值
det = f * det * elements[numColumns * numColumns - 1];
return (det);
}
/**
* 求矩阵秩的全选主元高斯消去法
*
* @return int型,矩阵的秩
*/
public int ComputeRankGauss()
{
int i, j, k, nn, nis = 0, js = 0, l, ll, u, v;
double q, d;
// 秩小于等于行列数
nn = numRows;
if (numRows >= numColumns)
nn = numColumns;
k = 0;
// 消元求解
for (l = 0; l <= nn - 1; l++)
{
q = 0.0;
for (i = l; i <= numRows - 1; i++)
{
for (j = l; j <= numColumns - 1; j++)
{
ll = i * numColumns + j;
d = Math.Abs(elements[ll]);
if (d > q)
{
q = d;
nis = i;
js = j;
}
}
}
if (q == 0.0)
return (k);
k = k + 1;
if (nis != l)
{
for (j = l; j <= numColumns - 1; j++)
{
u = l * numColumns + j;
v = nis * numColumns + j;
d = elements[u];
elements[u] = elements[v];
elements[v] = d;
}
}
if (js != l)
{
for (i = l; i <= numRows - 1; i++)
{
u = i * numColumns + js;
v = i * numColumns + l;
d = elements[u];
elements[u] = elements[v];
elements[v] = d;
}
}
ll = l * numColumns + l;
for (i = l + 1; i <= numColumns - 1; i++)
{
d = elements[i * numColumns + l] / elements[ll];
for (j = l + 1; j <= numColumns - 1; j++)
{
u = i * numColumns + j;
elements[u] = elements[u] - d * elements[l * numColumns + j];
}
}
}
return (k);
}
/**
* 对称正定矩阵的乔里斯基分解与行列式的求值
*
* @param realDetValue - 返回行列式的值
* @return bool型,求解是否成功
*/
public bool ComputeDetCholesky(ref double realDetValue)
{
int i, j, k, u, l;
double d;
// 不满足求解要求
if (elements[0] <= 0.0)
return false;
// 乔里斯基分解
elements[0] = Math.Sqrt(elements[0]);
d = elements[0];
for (i = 1; i <= numColumns - 1; i++)
{
u = i * numColumns;
elements[u] = elements[u] / elements[0];
}
for (j = 1; j <= numColumns - 1; j++)
{
l = j * numColumns + j;
for (k = 0; k <= j - 1; k++)
{
u = j * numColumns + k;
elements[l] = elements[l] - elements[u] * elements[u];
}
if (elements[l] <= 0.0)
return false;
elements[l] = Math.Sqrt(elements[l]);
d = d * elements[l];
for (i = j + 1; i <= numColumns - 1; i++)
{
u = i * numColumns + j;
for (k = 0; k <= j - 1; k++)
elements[u] = elements[u] - elements[i * numColumns + k] * elements[j * numColumns + k];
elements[u] = elements[u] / elements[l];
}
}
// 行列式求值
realDetValue = d * d;
// 下三角矩阵
for (i = 0; i <= numColumns - 2; i++)
for (j = i + 1; j <= numColumns - 1; j++)
elements[i * numColumns + j] = 0.0;
return true;
}
/**
* 矩阵的三角分解,分解成功后,原矩阵将成为Q矩阵
*
* @param mtxL - 返回分解后的L矩阵
* @param mtxU - 返回分解后的U矩阵
* @return bool型,求解是否成功
*/
public bool SplitLU(Matrix mtxL, Matrix mtxU)
{
int i, j, k, w, v, ll;
// 初始化结果矩阵
if (!mtxL.Init(numColumns, numColumns) ||
!mtxU.Init(numColumns, numColumns))
return false;
for (k = 0; k <= numColumns - 2; k++)
{
ll = k * numColumns + k;
if (elements[ll] == 0.0)
return false;
for (i = k + 1; i <= numColumns - 1; i++)
{
w = i * numColumns + k;
elements[w] = elements[w] / elements[ll];
}
for (i = k + 1; i <= numColumns - 1; i++)
{
w = i * numColumns + k;
for (j = k + 1; j <= numColumns - 1; j++)
{
v = i * numColumns + j;
elements[v] = elements[v] - elements[w] * elements[k * numColumns + j];
}
}
}
for (i = 0; i <= numColumns - 1; i++)
{
for (j = 0; j < i; j++)
{
w = i * numColumns + j;
mtxL.elements[w] = elements[w];
mtxU.elements[w] = 0.0;
}
w = i * numColumns + i;
mtxL.elements[w] = 1.0;
mtxU.elements[w] = elements[w];
for (j = i + 1; j <= numColumns - 1; j++)
{
w = i * numColumns + j;
mtxL.elements[w] = 0.0;
mtxU.elements[w] = elements[w];
}
}
return true;
}
/**
* 一般实矩阵的QR分解,分解成功后,原矩阵将成为R矩阵
*
* @param mtxQ - 返回分解后的Q矩阵
* @return bool型,求解是否成功
*/
public bool SplitQR(Matrix mtxQ)
{
int i, j, k, l, nn, p, jj;
double u, alpha, w, t;
if (numRows < numColumns)
return false;
// 初始化Q矩阵
if (!mtxQ.Init(numRows, numRows))
return false;
// 对角线元素单位化
for (i = 0; i <= numRows - 1; i++)
{
for (j = 0; j <= numRows - 1; j++)
{
l = i * numRows + j;
mtxQ.elements[l] = 0.0;
if (i == j)
mtxQ.elements[l] = 1.0;
}
}
// 开始分解
nn = numColumns;
if (numRows == numColumns)
nn = numRows - 1;
for (k = 0; k <= nn - 1; k++)
{
u = 0.0;
l = k * numColumns + k;
for (i = k; i <= numRows - 1; i++)
{
w = Math.Abs(elements[i * numColumns + k]);
if (w > u)
u = w;
}
alpha = 0.0;
for (i = k; i <= numRows - 1; i++)
{
t = elements[i * numColumns + k] / u;
alpha = alpha + t * t;
}
if (elements[l] > 0.0)
u = -u;
alpha = u * Math.Sqrt(alpha);
if (alpha == 0.0)
return false;
u = Math.Sqrt(2.0 * alpha * (alpha - elements[l]));
if ((u + 1.0) != 1.0)
{
elements[l] = (elements[l] - alpha) / u;
for (i = k + 1; i <= numRows - 1; i++)
{
p = i * numColumns + k;
elements[p] = elements[p] / u;
}
for (j = 0; j <= numRows - 1; j++)
{
t = 0.0;
for (jj = k; jj <= numRows - 1; jj++)
t = t + elements[jj * numColumns + k] * mtxQ.elements[jj * numRows + j];
for (i = k; i <= numRows - 1; i++)
{
p = i * numRows + j;
mtxQ.elements[p] = mtxQ.elements[p] - 2.0 * t * elements[i * numColumns + k];
}
}
for (j = k + 1; j <= numColumns - 1; j++)
{
t = 0.0;
for (jj = k; jj <= numRows - 1; jj++)
t = t + elements[jj * numColumns + k] * elements[jj * numColumns + j];
for (i = k; i <= numRows - 1; i++)
{
p = i * numColumns + j;
elements[p] = elements[p] - 2.0 * t * elements[i * numColumns + k];
}
}
elements[l] = alpha;
for (i = k + 1; i <= numRows - 1; i++)
elements[i * numColumns + k] = 0.0;
}
}
// 调整元素
for (i = 0; i <= numRows - 2; i++)
{
for (j = i + 1; j <= numRows - 1; j++)
{
p = i * numRows + j;
l = j * numRows + i;
t = mtxQ.elements[p];
mtxQ.elements[p] = mtxQ.elements[l];
mtxQ.elements[l] = t;
}
}
return true;
}
/**
* 一般实矩阵的奇异值分解,分解成功后,原矩阵对角线元素就是矩阵的奇异值
*
* @param mtxU - 返回分解后的U矩阵
* @param mtxV - 返回分解后的V矩阵
* @param eps - 计算精度
* @return bool型,求解是否成功
*/
public bool SplitUV(Matrix mtxU, Matrix mtxV, double eps)
{
int i, j, k, l, it, ll, kk, ix, iy, mm, nn, iz, m1, ks;
double d, dd, t, sm, sm1, em1, sk, ek, b, c, shh;
double[] fg = new double[2];
double[] cs = new double[2];
int m = numRows;
int n = numColumns;
// 初始化U, V矩阵
if (!mtxU.Init(m, m) || !mtxV.Init(n, n))
return false;
// 临时缓冲区
int ka = Math.Max(m, n) + 1;
double[] s = new double[ka];
double[] e = new double[ka];
double[] w = new double[ka];
// 指定迭代次数为60
it = 60;
k = n;
if (m - 1 < n)
k = m - 1;
l = m;
if (n - 2 < m)
l = n - 2;
if (l < 0)
l = 0;
// 循环迭代计算
ll = k;
if (l > k)
ll = l;
if (ll >= 1)
{
for (kk = 1; kk <= ll; kk++)
{
if (kk <= k)
{
d = 0.0;
for (i = kk; i <= m; i++)
{
ix = (i - 1) * n + kk - 1;
d = d + elements[ix] * elements[ix];
}
s[kk - 1] = Math.Sqrt(d);
if (s[kk - 1] != 0.0)
{
ix = (kk - 1) * n + kk - 1;
if (elements[ix] != 0.0)
{
s[kk - 1] = Math.Abs(s[kk - 1]);
if (elements[ix] < 0.0)
s[kk - 1] = -s[kk - 1];
}
for (i = kk; i <= m; i++)
{
iy = (i - 1) * n + kk - 1;
elements[iy] = elements[iy] / s[kk - 1];
}
elements[ix] = 1.0 + elements[ix];
}
s[kk - 1] = -s[kk - 1];
}
if (n >= kk + 1)
{
for (j = kk + 1; j <= n; j++)
{
if ((kk <= k) && (s[kk - 1] != 0.0))
{
d = 0.0;
for (i = kk; i <= m; i++)
{
ix = (i - 1) * n + kk - 1;
iy = (i - 1) * n + j - 1;
d = d + elements[ix] * elements[iy];
}
d = -d / elements[(kk - 1) * n + kk - 1];
for (i = kk; i <= m; i++)
{
ix = (i - 1) * n + j - 1;
iy = (i - 1) * n + kk - 1;
elements[ix] = elements[ix] + d * elements[iy];
}
}
e[j - 1] = elements[(kk - 1) * n + j - 1];
}
}
if (kk <= k)
{
for (i = kk; i <= m; i++)
{
ix = (i - 1) * m + kk - 1;
iy = (i - 1) * n + kk - 1;
mtxU.elements[ix] = elements[iy];
}
}
if (kk <= l)
{
d = 0.0;
for (i = kk + 1; i <= n; i++)
d = d + e[i - 1] * e[i - 1];
e[kk - 1] = Math.Sqrt(d);
if (e[kk - 1] != 0.0)
{
if (e[kk] != 0.0)
{
e[kk - 1] = Math.Abs(e[kk - 1]);
if (e[kk] < 0.0)
e[kk - 1] = -e[kk - 1];
}
for (i = kk + 1; i <= n; i++)
e[i - 1] = e[i - 1] / e[kk - 1];
e[kk] = 1.0 + e[kk];
}
e[kk - 1] = -e[kk - 1];
if ((kk + 1 <= m) && (e[kk - 1] != 0.0))
{
for (i = kk + 1; i <= m; i++)
w[i - 1] = 0.0;
for (j = kk + 1; j <= n; j++)
for (i = kk + 1; i <= m; i++)
w[i - 1] = w[i - 1] + e[j - 1] * elements[(i - 1) * n + j - 1];
for (j = kk + 1; j <= n; j++)
{
for (i = kk + 1; i <= m; i++)
{
ix = (i - 1) * n + j - 1;
elements[ix] = elements[ix] - w[i - 1] * e[j - 1] / e[kk];
}
}
}
for (i = kk + 1; i <= n; i++)
mtxV.elements[(i - 1) * n + kk - 1] = e[i - 1];
}
}
}
mm = n;
if (m + 1 < n)
mm = m + 1;
if (k < n)
s[k] = elements[k * n + k];
if (m < mm)
s[mm - 1] = 0.0;
if (l + 1 < mm)
e[l] = elements[l * n + mm - 1];
e[mm - 1] = 0.0;
nn = m;
if (m > n)
nn = n;
if (nn >= k + 1)
{
for (j = k + 1; j <= nn; j++)
{
for (i = 1; i <= m; i++)
mtxU.elements[(i - 1) * m + j - 1] = 0.0;
mtxU.elements[(j - 1) * m + j - 1] = 1.0;
}
}
if (k >= 1)
{
for (ll = 1; ll <= k; ll++)
{
kk = k - ll + 1;
iz = (kk - 1) * m + kk - 1;
if (s[kk - 1] != 0.0)
{
if (nn >= kk + 1)
{
for (j = kk + 1; j <= nn; j++)
{
d = 0.0;
for (i = kk; i <= m; i++)
{
ix = (i - 1) * m + kk - 1;
iy = (i - 1) * m + j - 1;
d = d + mtxU.elements[ix] * mtxU.elements[iy] / mtxU.elements[iz];
}
d = -d;
for (i = kk; i <= m; i++)
{
ix = (i - 1) * m + j - 1;
iy = (i - 1) * m + kk - 1;
mtxU.elements[ix] = mtxU.elements[ix] + d * mtxU.elements[iy];
}
}
}
for (i = kk; i <= m; i++)
{
ix = (i - 1) * m + kk - 1;
mtxU.elements[ix] = -mtxU.elements[ix];
}
mtxU.elements[iz] = 1.0 + mtxU.elements[iz];
if (kk - 1 >= 1)
{
for (i = 1; i <= kk - 1; i++)
mtxU.elements[(i - 1) * m + kk - 1] = 0.0;
}
}
else
{
for (i = 1; i <= m; i++)
mtxU.elements[(i - 1) * m + kk - 1] = 0.0;
mtxU.elements[(kk - 1) * m + kk - 1] = 1.0;
}
}
}
for (ll = 1; ll <= n; ll++)
{
kk = n - ll + 1;
iz = kk * n + kk - 1;
if ((kk <= l) && (e[kk - 1] != 0.0))
{
for (j = kk + 1; j <= n; j++)
{
d = 0.0;
for (i = kk + 1; i <= n; i++)
{
ix = (i - 1) * n + kk - 1;
iy = (i - 1) * n + j - 1;
d = d + mtxV.elements[ix] * mtxV.elements[iy] / mtxV.elements[iz];
}
d = -d;
for (i = kk + 1; i <= n; i++)
{
ix = (i - 1) * n + j - 1;
iy = (i - 1) * n + kk - 1;
mtxV.elements[ix] = mtxV.elements[ix] + d * mtxV.elements[iy];
}
}
}
for (i = 1; i <= n; i++)
mtxV.elements[(i - 1) * n + kk - 1] = 0.0;
mtxV.elements[iz - n] = 1.0;
}
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++)
elements[(i - 1) * n + j - 1] = 0.0;
m1 = mm;
it = 60;
while (true)
{
if (mm == 0)
{
ppp(elements, e, s, mtxV.elements, m, n);
return true;
}
if (it == 0)
{
ppp(elements, e, s, mtxV.elements, m, n);
return false;
}
kk = mm - 1;
while ((kk != 0) && (Math.Abs(e[kk - 1]) != 0.0))
{
d = Math.Abs(s[kk - 1]) + Math.Abs(s[kk]);
dd = Math.Abs(e[kk - 1]);
if (dd > eps * d)
kk = kk - 1;
else
e[kk - 1] = 0.0;
}
if (kk == mm - 1)
{
kk = kk + 1;
if (s[kk - 1] < 0.0)
{
s[kk - 1] = -s[kk - 1];
for (i = 1; i <= n; i++)
{
ix = (i - 1) * n + kk - 1;
mtxV.elements[ix] = -mtxV.elements[ix];
}
}
while ((kk != m1) && (s[kk - 1] < s[kk]))
{
d = s[kk - 1];
s[kk - 1] = s[kk];
s[kk] = d;
if (kk < n)
{
for (i = 1; i <= n; i++)
{
ix = (i - 1) * n + kk - 1;
iy = (i - 1) * n + kk;
d = mtxV.elements[ix];
mtxV.elements[ix] = mtxV.elements[iy];
mtxV.elements[iy] = d;
}
}
if (kk < m)
{
for (i = 1; i <= m; i++)
{
ix = (i - 1) * m + kk - 1;
iy = (i - 1) * m + kk;
d = mtxU.elements[ix];
mtxU.elements[ix] = mtxU.elements[iy];
mtxU.elements[iy] = d;
}
}
kk = kk + 1;
}
it = 60;
mm = mm - 1;
}
else
{
ks = mm;
while ((ks > kk) && (Math.Abs(s[ks - 1]) != 0.0))
{
d = 0.0;
if (ks != mm)
d = d + Math.Abs(e[ks - 1]);
if (ks != kk + 1)
d = d + Math.Abs(e[ks - 2]);
dd = Math.Abs(s[ks - 1]);
if (dd > eps * d)
ks = ks - 1;
else
s[ks - 1] = 0.0;
}
if (ks == kk)
{
kk = kk + 1;
d = Math.Abs(s[mm - 1]);
t = Math.Abs(s[mm - 2]);
if (t > d)
d = t;
t = Math.Abs(e[mm - 2]);
if (t > d)
d = t;
t = Math.Abs(s[kk - 1]);
if (t > d)
d = t;
t = Math.Abs(e[kk - 1]);
if (t > d)
d = t;
sm = s[mm - 1] / d;
sm1 = s[mm - 2] / d;
em1 = e[mm - 2] / d;
sk = s[kk - 1] / d;
ek = e[kk - 1] / d;
b = ((sm1 + sm) * (sm1 - sm) + em1 * em1) / 2.0;
c = sm * em1;
c = c * c;
shh = 0.0;
if ((b != 0.0) || (c != 0.0))
{
shh = Math.Sqrt(b * b + c);
if (b < 0.0)
shh = -shh;
shh = c / (b + shh);
}
fg[0] = (sk + sm) * (sk - sm) - shh;
fg[1] = sk * ek;
for (i = kk; i <= mm - 1; i++)
{
sss(fg, cs);
if (i != kk)
e[i - 2] = fg[0];
fg[0] = cs[0] * s[i - 1] + cs[1] * e[i - 1];
e[i - 1] = cs[0] * e[i - 1] - cs[1] * s[i - 1];
fg[1] = cs[1] * s[i];
s[i] = cs[0] * s[i];
if ((cs[0] != 1.0) || (cs[1] != 0.0))
{
for (j = 1; j <= n; j++)
{
ix = (j - 1) * n + i - 1;
iy = (j - 1) * n + i;
d = cs[0] * mtxV.elements[ix] + cs[1] * mtxV.elements[iy];
mtxV.elements[iy] = -cs[1] * mtxV.elements[ix] + cs[0] * mtxV.elements[iy];
mtxV.elements[ix] = d;
}
}
sss(fg, cs);
s[i - 1] = fg[0];
fg[0] = cs[0] * e[i - 1] + cs[1] * s[i];
s[i] = -cs[1] * e[i - 1] + cs[0] * s[i];
fg[1] = cs[1] * e[i];
e[i] = cs[0] * e[i];
if (i < m)
{
if ((cs[0] != 1.0) || (cs[1] != 0.0))
{
for (j = 1; j <= m; j++)
{
ix = (j - 1) * m + i - 1;
iy = (j - 1) * m + i;
d = cs[0] * mtxU.elements[ix] + cs[1] * mtxU.elements[iy];
mtxU.elements[iy] = -cs[1] * mtxU.elements[ix] + cs[0] * mtxU.elements[iy];
mtxU.elements[ix] = d;
}
}
}
}
e[mm - 2] = fg[0];
it = it - 1;
}
else
{
if (ks == mm)
{
kk = kk + 1;
fg[1] = e[mm - 2];
e[mm - 2] = 0.0;
for (ll = kk; ll <= mm - 1; ll++)
{
i = mm + kk - ll - 1;
fg[0] = s[i - 1];
sss(fg, cs);
s[i - 1] = fg[0];
if (i != kk)
{
fg[1] = -cs[1] * e[i - 2];
e[i - 2] = cs[0] * e[i - 2];
}
if ((cs[0] != 1.0) || (cs[1] != 0.0))
{
for (j = 1; j <= n; j++)
{
ix = (j - 1) * n + i - 1;
iy = (j - 1) * n + mm - 1;
d = cs[0] * mtxV.elements[ix] + cs[1] * mtxV.elements[iy];
mtxV.elements[iy] = -cs[1] * mtxV.elements[ix] + cs[0] * mtxV.elements[iy];
mtxV.elements[ix] = d;
}
}
}
}
else
{
kk = ks + 1;
fg[1] = e[kk - 2];
e[kk - 2] = 0.0;
for (i = kk; i <= mm; i++)
{
fg[0] = s[i - 1];
sss(fg, cs);
s[i - 1] = fg[0];
fg[1] = -cs[1] * e[i - 1];
e[i - 1] = cs[0] * e[i - 1];
if ((cs[0] != 1.0) || (cs[1] != 0.0))
{
for (j = 1; j <= m; j++)
{
ix = (j - 1) * m + i - 1;
iy = (j - 1) * m + kk - 2;
d = cs[0] * mtxU.elements[ix] + cs[1] * mtxU.elements[iy];
mtxU.elements[iy] = -cs[1] * mtxU.elements[ix] + cs[0] * mtxU.elements[iy];
mtxU.elements[ix] = d;
}
}
}
}
}
}
}
}
/**
* 内部函数,由SplitUV函数调用
*/
private void ppp(double[] a, double[] e, double[] s, double[] v, int m, int n)
{
int i, j, p, q;
double d;
if (m >= n)
i = n;
else
i = m;
for (j = 1; j <= i - 1; j++)
{
a[(j - 1) * n + j - 1] = s[j - 1];
a[(j - 1) * n + j] = e[j - 1];
}
a[(i - 1) * n + i - 1] = s[i - 1];
if (m < n)
a[(i - 1) * n + i] = e[i - 1];
for (i = 1; i <= n - 1; i++)
{
for (j = i + 1; j <= n; j++)
{
p = (i - 1) * n + j - 1;
q = (j - 1) * n + i - 1;
d = v[p];
v[p] = v[q];
v[q] = d;
}
}
}
/**
* 内部函数,由SplitUV函数调用
*/
private void sss(double[] fg, double[] cs)
{
double r, d;
if ((Math.Abs(fg[0]) + Math.Abs(fg[1])) == 0.0)
{
cs[0] = 1.0;
cs[1] = 0.0;
d = 0.0;
}
else
{
d = Math.Sqrt(fg[0] * fg[0] + fg[1] * fg[1]);
if (Math.Abs(fg[0]) > Math.Abs(fg[1]))
{
d = Math.Abs(d);
if (fg[0] < 0.0)
d = -d;
}
if (Math.Abs(fg[1]) >= Math.Abs(fg[0]))
{
d = Math.Abs(d);
if (fg[1] < 0.0)
d = -d;
}
cs[0] = fg[0] / d;
cs[1] = fg[1] / d;
}
r = 1.0;
if (Math.Abs(fg[0]) > Math.Abs(fg[1]))
r = cs[1];
else if (cs[0] != 0.0)
r = 1.0 / cs[0];
fg[0] = d;
fg[1] = r;
}
/**
* 求广义逆的奇异值分解法,分解成功后,原矩阵对角线元素就是矩阵的奇异值
*
* @param mtxAP - 返回原矩阵的广义逆矩阵
* @param mtxU - 返回分解后的U矩阵
* @param mtxV - 返回分解后的V矩阵
* @param eps - 计算精度
* @return bool型,求解是否成功
*/
public bool InvertUV(Matrix mtxAP, Matrix mtxU, Matrix mtxV, double eps)
{
int i, j, k, l, t, p, q, f;
// 调用奇异值分解
if (!SplitUV(mtxU, mtxV, eps))
return false;
int m = numRows;
int n = numColumns;
// 初始化广义逆矩阵
if (!mtxAP.Init(n, m))
return false;
// 计算广义逆矩阵
j = n;
if (m < n)
j = m;
j = j - 1;
k = 0;
while ((k <= j) && (elements[k * n + k] != 0.0))
k = k + 1;
k = k - 1;
for (i = 0; i <= n - 1; i++)
{
for (j = 0; j <= m - 1; j++)
{
t = i * m + j;
mtxAP.elements[t] = 0.0;
for (l = 0; l <= k; l++)
{
f = l * n + i;
p = j * m + l;
q = l * n + l;
mtxAP.elements[t] = mtxAP.elements[t] + mtxV.elements[f] * mtxU.elements[p] / elements[q];
}
}
}
return true;
}
/**
* 约化对称矩阵为对称三对角阵的豪斯荷尔德变换法
*
* @param mtxQ - 返回豪斯荷尔德变换的乘积矩阵Q
* @param mtxT - 返回求得的对称三对角阵
* @param dblB - 一维数组,长度为矩阵的阶数,返回对称三对角阵的主对角线元素
* @param dblC - 一维数组,长度为矩阵的阶数,前n-1个元素返回对称三对角阵的
* 次对角线元素
* @return bool型,求解是否成功
*/
public bool MakeSymTri(Matrix mtxQ, Matrix mtxT, double[] dblB, double[] dblC)
{
int i, j, k, u;
double h, f, g, h2;
// 初始化矩阵Q和T
if (!mtxQ.Init(numColumns, numColumns) ||
!mtxT.Init(numColumns, numColumns))
return false;
if (dblB == null || dblC == null)
return false;
for (i = 0; i <= numColumns - 1; i++)
{
for (j = 0; j <= numColumns - 1; j++)
{
u = i * numColumns + j;
mtxQ.elements[u] = elements[u];
}
}
for (i = numColumns - 1; i >= 1; i--)
{
h = 0.0;
if (i > 1)
{
for (k = 0; k <= i - 1; k++)
{
u = i * numColumns + k;
h = h + mtxQ.elements[u] * mtxQ.elements[u];
}
}
if (h == 0.0)
{
dblC[i] = 0.0;
if (i == 1)
dblC[i] = mtxQ.elements[i * numColumns + i - 1];
dblB[i] = 0.0;
}
else
{
dblC[i] = Math.Sqrt(h);
u = i * numColumns + i - 1;
if (mtxQ.elements[u] > 0.0)
dblC[i] = -dblC[i];
h = h - mtxQ.elements[u] * dblC[i];
mtxQ.elements[u] = mtxQ.elements[u] - dblC[i];
f = 0.0;
for (j = 0; j <= i - 1; j++)
{
mtxQ.elements[j * numColumns + i] = mtxQ.elements[i * numColumns + j] / h;
g = 0.0;
for (k = 0; k <= j; k++)
g = g + mtxQ.elements[j * numColumns + k] * mtxQ.elements[i * numColumns + k];
if (j + 1 <= i - 1)
for (k = j + 1; k <= i - 1; k++)
g = g + mtxQ.elements[k * numColumns + j] * mtxQ.elements[i * numColumns + k];
dblC[j] = g / h;
f = f + g * mtxQ.elements[j * numColumns + i];
}
h2 = f / (h + h);
for (j = 0; j <= i - 1; j++)
{
f = mtxQ.elements[i * numColumns + j];
g = dblC[j] - h2 * f;
dblC[j] = g;
for (k = 0; k <= j; k++)
{
u = j * numColumns + k;
mtxQ.elements[u] = mtxQ.elements[u] - f * dblC[k] - g * mtxQ.elements[i * numColumns + k];
}
}
dblB[i] = h;
}
}
for (i = 0; i <= numColumns - 2; i++)
dblC[i] = dblC[i + 1];
dblC[numColumns - 1] = 0.0;
dblB[0] = 0.0;
for (i = 0; i <= numColumns - 1; i++)
{
if ((dblB[i] != (double)0.0) && (i - 1 >= 0))
{
for (j = 0; j <= i - 1; j++)
{
g = 0.0;
for (k = 0; k <= i - 1; k++)
g = g + mtxQ.elements[i * numColumns + k] * mtxQ.elements[k * numColumns + j];
for (k = 0; k <= i - 1; k++)
{
u = k * numColumns + j;
mtxQ.elements[u] = mtxQ.elements[u] - g * mtxQ.elements[k * numColumns + i];
}
}
}
u = i * numColumns + i;
dblB[i] = mtxQ.elements[u]; mtxQ.elements[u] = 1.0;
if (i - 1 >= 0)
{
for (j = 0; j <= i - 1; j++)
{
mtxQ.elements[i * numColumns + j] = 0.0;
mtxQ.elements[j * numColumns + i] = 0.0;
}
}
}
// 构造对称三对角矩阵
for (i = 0; i < numColumns; ++i)
{
for (j = 0; j < numColumns; ++j)
{
mtxT.SetElement(i, j, 0);
k = i - j;
if (k == 0)
mtxT.SetElement(i, j, dblB[j]);
else if (k == 1)
mtxT.SetElement(i, j, dblC[j]);
else if (k == -1)
mtxT.SetElement(i, j, dblC[i]);
}
}
return true;
}
/**
* 实对称三对角阵的全部特征值与特征向量的计算
*
* @param dblB - 一维数组,长度为矩阵的阶数,传入对称三对角阵的主对角线元素;
* 返回时存放全部特征值。
* @param dblC - 一维数组,长度为矩阵的阶数,前n-1个元素传入对称三对角阵的
* 次对角线元素
* @param mtxQ - 如果传入单位矩阵,则返回实对称三对角阵的特征值向量矩阵;
* 如果传入MakeSymTri函数求得的矩阵A的豪斯荷尔德变换的乘积
* 矩阵Q,则返回矩阵A的特征值向量矩阵。其中第i列为与数组dblB
* 中第j个特征值对应的特征向量。
* @param nMaxIt - 迭代次数
* @param eps - 计算精度
* @return bool型,求解是否成功
*/
public bool ComputeEvSymTri(double[] dblB, double[] dblC, Matrix mtxQ, int nMaxIt, double eps)
{
int i, j, k, m, it, u, v;
double d, f, h, g, p, r, e, s;
// 初值
int n = mtxQ.GetNumColumns();
dblC[n - 1] = 0.0;
d = 0.0;
f = 0.0;
// 迭代计算
for (j = 0; j <= n - 1; j++)
{
it = 0;
h = eps * (Math.Abs(dblB[j]) + Math.Abs(dblC[j]));
if (h > d)
d = h;
m = j;
while ((m <= n - 1) && (Math.Abs(dblC[m]) > d))
m = m + 1;
if (m != j)
{
do
{
if (it == nMaxIt)
return false;
it = it + 1;
g = dblB[j];
p = (dblB[j + 1] - g) / (2.0 * dblC[j]);
r = Math.Sqrt(p * p + 1.0);
if (p >= 0.0)
dblB[j] = dblC[j] / (p + r);
else
dblB[j] = dblC[j] / (p - r);
h = g - dblB[j];
for (i = j + 1; i <= n - 1; i++)
dblB[i] = dblB[i] - h;
f = f + h;
p = dblB[m];
e = 1.0;
s = 0.0;
for (i = m - 1; i >= j; i--)
{
g = e * dblC[i];
h = e * p;
if (Math.Abs(p) >= Math.Abs(dblC[i]))
{
e = dblC[i] / p;
r = Math.Sqrt(e * e + 1.0);
dblC[i + 1] = s * p * r;
s = e / r;
e = 1.0 / r;
}
else
{
e = p / dblC[i];
r = Math.Sqrt(e * e + 1.0);
dblC[i + 1] = s * dblC[i] * r;
s = 1.0 / r;
e = e / r;
}
p = e * dblB[i] - s * g;
dblB[i + 1] = h + s * (e * g + s * dblB[i]);
for (k = 0; k <= n - 1; k++)
{
u = k * n + i + 1;
v = u - 1;
h = mtxQ.elements[u];
mtxQ.elements[u] = s * mtxQ.elements[v] + e * h;
mtxQ.elements[v] = e * mtxQ.elements[v] - s * h;
}
}
dblC[j] = s * p;
dblB[j] = e * p;
} while (Math.Abs(dblC[j]) > d);
}
dblB[j] = dblB[j] + f;
}
for (i = 0; i <= n - 1; i++)
{
k = i;
p = dblB[i];
if (i + 1 <= n - 1)
{
j = i + 1;
while ((j <= n - 1) && (dblB[j] <= p))
{
k = j;
p = dblB[j];
j = j + 1;
}
}
if (k != i)
{
dblB[k] = dblB[i];
dblB[i] = p;
for (j = 0; j <= n - 1; j++)
{
u = j * n + i;
v = j * n + k;
p = mtxQ.elements[u];
mtxQ.elements[u] = mtxQ.elements[v];
mtxQ.elements[v] = p;
}
}
}
return true;
}
/**
* 约化一般实矩阵为赫申伯格矩阵的初等相似变换法
*/
public void MakeHberg()
{
int i = 0, j, k, u, v;
double d, t;
for (k = 1; k <= numColumns - 2; k++)
{
d = 0.0;
for (j = k; j <= numColumns - 1; j++)
{
u = j * numColumns + k - 1;
t = elements[u];
if (Math.Abs(t) > Math.Abs(d))
{
d = t;
i = j;
}
}
if (d != 0.0)
{
if (i != k)
{
for (j = k - 1; j <= numColumns - 1; j++)
{
u = i * numColumns + j;
v = k * numColumns + j;
t = elements[u];
elements[u] = elements[v];
elements[v] = t;
}
for (j = 0; j <= numColumns - 1; j++)
{
u = j * numColumns + i;
v = j * numColumns + k;
t = elements[u];
elements[u] = elements[v];
elements[v] = t;
}
}
for (i = k + 1; i <= numColumns - 1; i++)
{
u = i * numColumns + k - 1;
t = elements[u] / d;
elements[u] = 0.0;
for (j = k; j <= numColumns - 1; j++)
{
v = i * numColumns + j;
elements[v] = elements[v] - t * elements[k * numColumns + j];
}
for (j = 0; j <= numColumns - 1; j++)
{
v = j * numColumns + k;
elements[v] = elements[v] + t * elements[j * numColumns + i];
}
}
}
}
}
/**
* 求赫申伯格矩阵全部特征值的QR方法
*
* @param dblU - 一维数组,长度为矩阵的阶数,返回时存放特征值的实部
* @param dblV - 一维数组,长度为矩阵的阶数,返回时存放特征值的虚部
* @param nMaxIt - 迭代次数
* @param eps - 计算精度
* @return bool型,求解是否成功
*/
public bool ComputeEvHBerg(double[] dblU, double[] dblV, int nMaxIt, double eps)
{
int m, it, i, j, k, l, ii, jj, kk, ll;
double b, c, w, g, xy, p, q, r, x, s, e, f, z, y;
int n = numColumns;
it = 0;
m = n;
while (m != 0)
{
l = m - 1;
while ((l > 0) && (Math.Abs(elements[l * n + l - 1]) >
eps * (Math.Abs(elements[(l - 1) * n + l - 1]) + Math.Abs(elements[l * n + l]))))
l = l - 1;
ii = (m - 1) * n + m - 1;
jj = (m - 1) * n + m - 2;
kk = (m - 2) * n + m - 1;
ll = (m - 2) * n + m - 2;
if (l == m - 1)
{
dblU[m - 1] = elements[(m - 1) * n + m - 1];
dblV[m - 1] = 0.0;
m = m - 1;
it = 0;
}
else if (l == m - 2)
{
b = -(elements[ii] + elements[ll]);
c = elements[ii] * elements[ll] - elements[jj] * elements[kk];
w = b * b - 4.0 * c;
y = Math.Sqrt(Math.Abs(w));
if (w > 0.0)
{
xy = 1.0;
if (b < 0.0)
xy = -1.0;
dblU[m - 1] = (-b - xy * y) / 2.0;
dblU[m - 2] = c / dblU[m - 1];
dblV[m - 1] = 0.0; dblV[m - 2] = 0.0;
}
else
{
dblU[m - 1] = -b / 2.0;
dblU[m - 2] = dblU[m - 1];
dblV[m - 1] = y / 2.0;
dblV[m - 2] = -dblV[m - 1];
}
m = m - 2;
it = 0;
}
else
{
if (it >= nMaxIt)
return false;
it = it + 1;
for (j = l + 2; j <= m - 1; j++)
elements[j * n + j - 2] = 0.0;
for (j = l + 3; j <= m - 1; j++)
elements[j * n + j - 3] = 0.0;
for (k = l; k <= m - 2; k++)
{
if (k != l)
{
p = elements[k * n + k - 1];
q = elements[(k + 1) * n + k - 1];
r = 0.0;
if (k != m - 2)
r = elements[(k + 2) * n + k - 1];
}
else
{
x = elements[ii] + elements[ll];
y = elements[ll] * elements[ii] - elements[kk] * elements[jj];
ii = l * n + l;
jj = l * n + l + 1;
kk = (l + 1) * n + l;
ll = (l + 1) * n + l + 1;
p = elements[ii] * (elements[ii] - x) + elements[jj] * elements[kk] + y;
q = elements[kk] * (elements[ii] + elements[ll] - x);
r = elements[kk] * elements[(l + 2) * n + l + 1];
}
if ((Math.Abs(p) + Math.Abs(q) + Math.Abs(r)) != 0.0)
{
xy = 1.0;
if (p < 0.0)
xy = -1.0;
s = xy * Math.Sqrt(p * p + q * q + r * r);
if (k != l)
elements[k * n + k - 1] = -s;
e = -q / s;
f = -r / s;
x = -p / s;
y = -x - f * r / (p + s);
g = e * r / (p + s);
z = -x - e * q / (p + s);
for (j = k; j <= m - 1; j++)
{
ii = k * n + j;
jj = (k + 1) * n + j;
p = x * elements[ii] + e * elements[jj];
q = e * elements[ii] + y * elements[jj];
r = f * elements[ii] + g * elements[jj];
if (k != m - 2)
{
kk = (k + 2) * n + j;
p = p + f * elements[kk];
q = q + g * elements[kk];
r = r + z * elements[kk];
elements[kk] = r;
}
elements[jj] = q; elements[ii] = p;
}
j = k + 3;
if (j >= m - 1)
j = m - 1;
for (i = l; i <= j; i++)
{
ii = i * n + k;
jj = i * n + k + 1;
p = x * elements[ii] + e * elements[jj];
q = e * elements[ii] + y * elements[jj];
r = f * elements[ii] + g * elements[jj];
if (k != m - 2)
{
kk = i * n + k + 2;
p = p + f * elements[kk];
q = q + g * elements[kk];
r = r + z * elements[kk];
elements[kk] = r;
}
elements[jj] = q;
elements[ii] = p;
}
}
}
}
}
return true;
}
/**
* 求实对称矩阵特征值与特征向量的雅可比法
*
* @param dblEigenValue - 一维数组,长度为矩阵的阶数,返回时存放特征值
* @param mtxEigenVector - 返回时存放特征向量矩阵,其中第i列为与数组
* dblEigenValue中第j个特征值对应的特征向量
* @param nMaxIt - 迭代次数
* @param eps - 计算精度
* @return bool型,求解是否成功
*/
public bool ComputeEvJacobi(double[] dblEigenValue, Matrix mtxEigenVector, int nMaxIt, double eps)
{
int i, j, p = 0, q = 0, u, w, t, s, l;
double fm, cn, sn, omega, x, y, d;
if (!mtxEigenVector.Init(numColumns, numColumns))
return false;
l = 1;
for (i = 0; i <= numColumns - 1; i++)
{
mtxEigenVector.elements[i * numColumns + i] = 1.0;
for (j = 0; j <= numColumns - 1; j++)
if (i != j)
mtxEigenVector.elements[i * numColumns + j] = 0.0;
}
while (true)
{
fm = 0.0;
for (i = 1; i <= numColumns - 1; i++)
{
for (j = 0; j <= i - 1; j++)
{
d = Math.Abs(elements[i * numColumns + j]);
if ((i != j) && (d > fm))
{
fm = d;
p = i;
q = j;
}
}
}
if (fm < eps)
{
for (i = 0; i < numColumns; ++i)
dblEigenValue[i] = GetElement(i, i);
return true;
}
if (l > nMaxIt)
return false;
l = l + 1;
u = p * numColumns + q;
w = p * numColumns + p;
t = q * numColumns + p;
s = q * numColumns + q;
x = -elements[u];
y = (elements[s] - elements[w]) / 2.0;
omega = x / Math.Sqrt(x * x + y * y);
if (y < 0.0)
omega = -omega;
sn = 1.0 + Math.Sqrt(1.0 - omega * omega);
sn = omega / Math.Sqrt(2.0 * sn);
cn = Math.Sqrt(1.0 - sn * sn);
fm = elements[w];
elements[w] = fm * cn * cn + elements[s] * sn * sn + elements[u] * omega;
elements[s] = fm * sn * sn + elements[s] * cn * cn - elements[u] * omega;
elements[u] = 0.0;
elements[t] = 0.0;
for (j = 0; j <= numColumns - 1; j++)
{
if ((j != p) && (j != q))
{
u = p * numColumns + j; w = q * numColumns + j;
fm = elements[u];
elements[u] = fm * cn + elements[w] * sn;
elements[w] = -fm * sn + elements[w] * cn;
}
}
for (i = 0; i <= numColumns - 1; i++)
{
if ((i != p) && (i != q))
{
u = i * numColumns + p;
w = i * numColumns + q;
fm = elements[u];
elements[u] = fm * cn + elements[w] * sn;
elements[w] = -fm * sn + elements[w] * cn;
}
}
for (i = 0; i <= numColumns - 1; i++)
{
u = i * numColumns + p;
w = i * numColumns + q;
fm = mtxEigenVector.elements[u];
mtxEigenVector.elements[u] = fm * cn + mtxEigenVector.elements[w] * sn;
mtxEigenVector.elements[w] = -fm * sn + mtxEigenVector.elements[w] * cn;
}
}
}
/**
* 求实对称矩阵特征值与特征向量的雅可比过关法
*
* @param dblEigenValue - 一维数组,长度为矩阵的阶数,返回时存放特征值
* @param mtxEigenVector - 返回时存放特征向量矩阵,其中第i列为与数组
* dblEigenValue中第j个特征值对应的特征向量
* @param eps - 计算精度
* @return bool型,求解是否成功
*/
public bool ComputeEvJacobi(double[] dblEigenValue, Matrix mtxEigenVector, double eps)
{
int i, j, p, q, u, w, t, s;
double ff, fm, cn, sn, omega, x, y, d;
if (!mtxEigenVector.Init(numColumns, numColumns))
return false;
for (i = 0; i <= numColumns - 1; i++)
{
mtxEigenVector.elements[i * numColumns + i] = 1.0;
for (j = 0; j <= numColumns - 1; j++)
if (i != j)
mtxEigenVector.elements[i * numColumns + j] = 0.0;
}
ff = 0.0;
for (i = 1; i <= numColumns - 1; i++)
{
for (j = 0; j <= i - 1; j++)
{
d = elements[i * numColumns + j];
ff = ff + d * d;
}
}
ff = Math.Sqrt(2.0 * ff);
ff = ff / (1.0 * numColumns);
bool nextLoop = false;
while (true)
{
for (i = 1; i <= numColumns - 1; i++)
{
for (j = 0; j <= i - 1; j++)
{
d = Math.Abs(elements[i * numColumns + j]);
if (d > ff)
{
p = i;
q = j;
u = p * numColumns + q;
w = p * numColumns + p;
t = q * numColumns + p;
s = q * numColumns + q;
x = -elements[u];
y = (elements[s] - elements[w]) / 2.0;
omega = x / Math.Sqrt(x * x + y * y);
if (y < 0.0)
omega = -omega;
sn = 1.0 + Math.Sqrt(1.0 - omega * omega);
sn = omega / Math.Sqrt(2.0 * sn);
cn = Math.Sqrt(1.0 - sn * sn);
fm = elements[w];
elements[w] = fm * cn * cn + elements[s] * sn * sn + elements[u] * omega;
elements[s] = fm * sn * sn + elements[s] * cn * cn - elements[u] * omega;
elements[u] = 0.0; elements[t] = 0.0;
for (j = 0; j <= numColumns - 1; j++)
{
if ((j != p) && (j != q))
{
u = p * numColumns + j;
w = q * numColumns + j;
fm = elements[u];
elements[u] = fm * cn + elements[w] * sn;
elements[w] = -fm * sn + elements[w] * cn;
}
}
for (i = 0; i <= numColumns - 1; i++)
{
if ((i != p) && (i != q))
{
u = i * numColumns + p;
w = i * numColumns + q;
fm = elements[u];
elements[u] = fm * cn + elements[w] * sn;
elements[w] = -fm * sn + elements[w] * cn;
}
}
for (i = 0; i <= numColumns - 1; i++)
{
u = i * numColumns + p;
w = i * numColumns + q;
fm = mtxEigenVector.elements[u];
mtxEigenVector.elements[u] = fm * cn + mtxEigenVector.elements[w] * sn;
mtxEigenVector.elements[w] = -fm * sn + mtxEigenVector.elements[w] * cn;
}
nextLoop = true;
break;
}
}
if (nextLoop)
break;
}
if (nextLoop)
{
nextLoop = false;
continue;
}
nextLoop = false;
// 如果达到精度要求,退出循环,返回结果
if (ff < eps)
{
for (i = 0; i < numColumns; ++i)
dblEigenValue[i] = GetElement(i, i);
return true;
}
ff = ff / (1.0 * numColumns);
}
}
}
}
源代码、示例数据及实验报告下载:https://pan.baidu.com/s/1HijfLR3YRbtAdZnMVCZDHg
提取码:wkbq
如果对你有帮助,就点个赞吧~
2022年10月25日更新
由于double类型精度较低,当坐标较大时拟合精度不高。遇到此问题的同学可以试下用matlab算,matlab处理数据精度很高。这里贴一下我写的m脚本的代码。这是二次拟合的代码,要用其他拟合模型可以自行在代码里更改公式。
clc
clear
close all
syms xy A L X n hang ;
xy=input("请输入坐标矩阵\n");
L=input("请输入高程异常矩阵\n");
hang=size(xy,1);%坐标矩阵行数
for n=1:hang
A(n,1)=1;
A(n,2)=xy(n,1);
A(n,3)=xy(n,2);
A(n,4)=xy(n,1)*xy(n,1);
A(n,5)=xy(n,1)*xy(n,2);
A(n,6)=xy(n,2)*xy(n,2);
end
X=(A'*A)\A'*L;%最小二乘计算参数
syms a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 L2 vv nei;
a1=X(1,1);
a2=X(2,1);
a3=X(3,1);
a4=X(4,1);
a5=X(5,1);
a6=X(6,1);
vv=0;
for n=1:hang%计算内符合精度
L2(n,1)=a1*A(n,1)+a2*A(n,2)+a3*A(n,3)+a4*A(n,4)+a5*A(n,5)+a6*A(n,6);
vv=vv+(L2(n,1)-L(n,1))*(L2(n,1)-L(n,1));
end
nei=sqrt(vv/(hang-1));%内符合精度
syms xy2 L3 L4 vv2 wai;
xy2=input("请输入检验点坐标矩阵\n");
L3=input("请输入检验点高程异常矩阵\n");
hang=size(xy2,1);
for n=1:hang
A(n,1)=1;
A(n,2)=xy2(n,1);
A(n,3)=xy2(n,2);
A(n,4)=xy2(n,1)*xy2(n,1);
A(n,5)=xy2(n,1)*xy2(n,2);
A(n,6)=xy2(n,2)*xy2(n,2);
end
vv2=0;
for n=1:hang%计算外符合精度
L4(n,1)=a1*A(n,1)+a2*A(n,2)+a3*A(n,3)+a4*A(n,4)+a5*A(n,5)+a6*A(n,6);
vv2=vv2+(L4(n,1)-L3(n,1))*(L4(n,1)-L3(n,1));
end
wai=sqrt(vv2/(hang-1));%外符合精度
syms xy3 L5;%进行高程拟合
xy3=input("请输入待拟合点坐标矩阵\n");
hang=size(xy3,1);
for n=1:hang
A(n,1)=1;
A(n,2)=xy3(n,1);
A(n,3)=xy3(n,2);
A(n,4)=xy3(n,1)*xy3(n,1);
A(n,5)=xy3(n,1)*xy3(n,2);
A(n,6)=xy3(n,2)*xy3(n,2);
end
for n=1:hang
L5(n,1)=a1*A(n,1)+a2*A(n,2)+a3*A(n,3)+a4*A(n,4)+a5*A(n,5)+a6*A(n,6);
end
%计算出来的结果是分数,使用vpa函数转换为小数形式输出
X=vpa(X)%拟合参数
nei=vpa(nei)%内符合精度
wai=vpa(wai)%外符合精度
L5=vpa(L5)%拟合结果
数据以矩阵形式输入,示例数据如下:
已知点:
[11862.976 698188.253;
10994.965 698400.600;
12565.437 698729.804;
11548.877 699010.132;
11295.099 699709.363;
12474.452 699730.173;
12269.934 700325.070;
13366.324 700571.591;
11680.564 700586.292;
10827.832 700816.915;
12219.760 701671.531;]
已知点高程异常:
[8.872;8.921;8.846;8.900;8.917;8.858;8.869;8.827;8.898;8.926;8.883]
检验点坐标:
[11455.209 698075.400;
11220.660 699117.203;
11250.595 701561.457;
13641.356 701563.181]
检验点高程异常:
[8.812;8.889;8.919;8.916;]
待拟合点坐标:
[12865.675 699245.085;
11567.390 700030.300;
12604.292 700210.577;
11254.665 700453.647;
12693.776 700538.770;
11185.344 700773.860;
12166.307 701039.320;
10357.026 701090.687;]