【算法】深度优先搜索 (DFS)

1.概述

（1）深度优先遍历 (Depth First Search, DFS)，是图的搜索算法之一，本质其实就是一个递归的过程，它就像是一棵树的前序遍历。

（2）DFS 从图中某个顶点 start 出发，访问此顶点，然后从 start 的未被访问的邻接点出发深度优先遍历图，直至图中所有和 start 有路径相通的顶点都被访问到。事实上这里讲到的是连通图，对于非连通图，只需要对它的连通分量分别进行深度优先遍历，即在先前一个顶点进行一次深度优先遍历后，若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

2.代码实现

（1）当使用邻接矩阵来表示图时，其代码实现如下：

class Solution {
	/*
    	adjMatrix 为邻接矩阵，adjMatrix[i][j] = 0 表示节点 i 和 j 之间没有边直接相连
    	start 为遍历的起点
	*/
    public void dfs(int[][] adjMatrix, int start) {
        // n 表示图中的节点数量，节点编号为 0 ~ n - 1
        int n = adjMatrix.length;
        //定义 visited 数组，防止对节点进行重复遍历
        boolean[] visited = new boolean[n];
        if (start < 0 || start > n - 1) {
            System.out.println("起点编号应为 [0, " + (n - 1) + "] 之间的整数！");
            return;
        }
        dfsTraverse(adjMatrix, start, visited);
    }
    
    private void dfsTraverse(int[][] adjMatrix, int node, boolean[] visited) {
        //标记当前访问到的节点
        visited[node] = true;
        System.out.print(node + " ");
        for (int i = 0; i < adjMatrix.length; i++) {
            //遍历邻接矩阵中第 node 行
            if (adjMatrix[node][i] != 0 && !visited[i]) {
                dfsTraverse(adjMatrix, i, visited);
            }
        }
    }
}

（2）当使用邻接表来表示图时，其代码实现如下：

class Solution {
 	/*
    	adjList 为邻接表，adjList[i] 中存储与节点 i 相邻的节点
    	start 为遍历的起点
	*/
    public void dfs(List<Integer>[] adjList, int start) {
        // n 表示图中的节点数量，节点编号为 0 ~ n - 1
        int n = adjList.length;
        //定义 visited 数组，防止对节点进行重复遍历
        boolean[] visited = new boolean[n];
        if (start < 0 || start > n - 1) {
            System.out.println("起点编号应为 [0, " + (n - 1) + "] 之间的整数！");
            return;
        }
        dfsTraverse(adjList, start, visited);
    }
    
    private void dfsTraverse(List<Integer>[] adjList, int node, boolean[] visited) {
        //标记当前访问到的节点
        visited[node] = true;
        System.out.print(node + " ");
        for (int nextNode : adjList[node]) {
            while (!visited[nextNode]) {
                dfsTraverse(adjList, nextNode, visited);
            }
        }
    }
}

（3）下面以图 G 为例来说明：

① 构造邻接矩阵：

int[][] adjMatrix = {
	        {0, 1, 1, 0, 1},
	        {1, 0, 0, 1, 1},
	        {1, 0, 0, 0, 1},
	        {0, 1, 0, 0, 1},
	        {1, 1, 1, 1, 0}
	};

② 构造邻接表：

int n = 5;
List<Integer>[] adjList = new ArrayList[n];
for (int i = 0; i < n; i++) {
    adjList[i] = new ArrayList<>();
}
adjList[0].add(1);
adjList[0].add(2);
adjList[0].add(4);
adjList[1].add(0);
adjList[1].add(3);
adjList[1].add(4);
adjList[2].add(0);
adjList[2].add(4);
adjList[3].add(1);
adjList[3].add(4);
adjList[4].add(0);
adjList[4].add(1);

如果 start = 2，那么遍历的节点依次为：

2 0 1 3 4

遍历过程如下图所示：

（3）DFS算法是一个递归算法，需要借助一个递归工作栈，故其空间复杂度为O(|V|)。遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间取决于所用的存储结构：

• 以邻接矩阵来表示时，查找每个顶点的邻接点所需的时间为 O(|V|)，故总的时间复杂度为 O(|V|²)
• 以邻接表来表示时，查找所有顶点的邻接点所需的时间为 O(|E|)，访问顶点所需的时间为 O(|V|)，此时，总的时间复杂度为 O(IV| + |E|)。

3.应用

（1）除了对图进行遍历以外，DFS 在求解图中是否存在路径中也有应用。

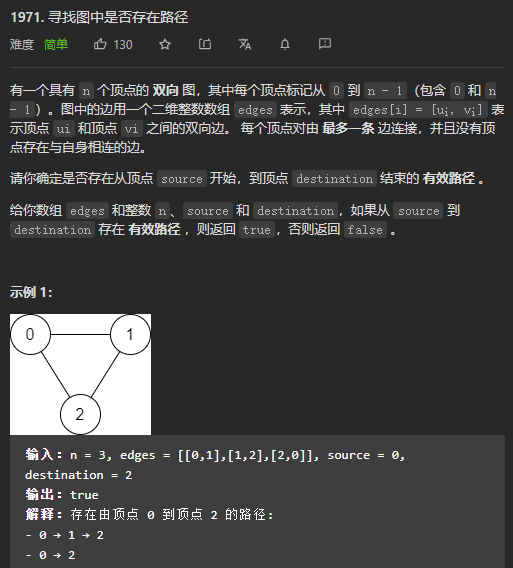
（2）以 LeetCode 中的1971.寻找图中是否存在路径这题为例：

分析如下：
① 根据题目所给的数组 edges 来构造邻接表 adj；
② 开始进行 DFS：
1）从起点 source 开始遍历并进行深度搜索，在搜索的过程中每访问到一个节点 v，如果该节点就是终点 destination，那么直接返回 true；
2）否则将其标记为已访问状态，并且继续递归访问与 v 相邻的下一个未访问节点 next，如果此时 next 与 destination 存在有效路径，那么说明起点 source 到终点 destination 之间也存在有效路径，此时直接返回 true 即可；
3）当访问完所有邻接节点后仍然没有访问到 destination，则返回 false。

具体代码实现如下：

public class Solution {
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        //构造邻接表
        List<Integer>[] adj = new List[n];
        for (int i = 0; i < n; i++) {
            adj[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            int x = edge[0];
            int y = edge[1];
            adj[x].add(y);
            adj[y].add(x);
        }
        // visited 用于标记每个节点是否已经被访问过
        boolean[] visited = new boolean[n];
        return dfs(source, destination, adj, visited);
    }
    
    //判断从起点 source 到终点 destination 是否存在有效路径，如果有则返回 true，否则返回 true
    private boolean dfs(int source, int destination, List<Integer>[] adj, boolean[] visited) {
        if (source == destination) {
            return true;
        } else {
            //标记当前访问到的节点
            visited[source] = true;
            for (int next : adj[source]) {
                while (!visited[next] && dfs(next, destination, adj, visited)) {
                    return true;
                }
            }
            return false;
        }
    }
}

（3）大家可以去 LeetCode 上找相关的 DFS 的题目来练习，或者也可以直接查看LeetCode算法刷题目录（Java）这篇文章中的 DFS 章节。如果大家发现文章中的错误之处，可在评论区中指出。