泛函分析中的向量空间

一、向量空间背景

(1) 具有如下点内积或标量内积的实数域$R$上的欧式空间$R^N$：
$$⟨\mathbf{u},\mathbf{v}⟩={\mathbf{u}}^{\mathrm{T}}\mathbf{v}=u_0{v}_0+u_1{v}_1+\cdots +u_{N-1}{v}_{N-1}=\sum _{i=0}^{N-1}{u}_i{v}_i$$

其中，$\mathbf{u}$和$\mathbf{v}$是$N\times 1$列向量。

(2) 具有如下内积函数的复数域$C$上的酉空间（unitary linear space）$C^N$：

$$⟨\mathbf{u},\mathbf{v}⟩={\mathbf{u}}^{\ast \mathrm{T}}\mathbf{v}=\sum _{i=0}^{N-1}{u}_i^{\ast }{v}_i=<\mathbf{v},\mathbf{u}{>}^{\ast }$$
(3) 内积空间$C([a,b])$， 其中向量是区间$a\le x\le b$上的连续函数， 内积函数是积分内积：

$$<f(x),g(x)>={\int }_a^b{f}^{\ast }(x)g(x)\mathrm{d}x$$

向量$z$的范数或长度为：
$$\Vert \mathbf{z}\Vert =\sqrt{⟨\mathbf{z},\mathbf{z}⟩}$$

若$z$的范数是1， 则称$z$是归一化的。

两个非零向量z和w之间的夹角为：
$$\theta =\arccos \frac{⟨\mathbf{z},\mathbf{w}⟩}{\Vert \mathbf{z}\Vert \Vert \mathbf{w}\Vert }$$
若$⟨\mathbf{z},\mathbf{w}⟩=0$，则称$z$和$w$是正交的(orthogonal)。即当且仅当
$$<{\mathbf{w}}_k,{\mathbf{w}}_l>=0,k\ne l$$

时， 非零向量$w_0,w_1,w_2,\cdots$是所张成内积空间的正交基。若基向量是归一化的，则它们是一个正交基，并且有
$$⟨{\mathbf{w}}_k,{\mathbf{w}}_l⟩={\delta }_{kl}=\{\begin{array}{l}0,k\ne l\\ 1,k=l\end{array}$$
类似地， 若
$$<{\tilde{\mathbf{w}}}_k,{\mathbf{w}}_l>=0,k\ne l$$
则称向量集合${\mathbf{w}}_0,{\mathbf{w}}_1,{\mathbf{w}}_2,\cdots$和对偶向量补集${\tilde{\mathbf{w}}}_0,{\tilde{\mathbf{w}}}_1,{\tilde{\mathbf{w}}}_2,\cdots$是双正交的，并且是所张成向量空间的一个双正交基。 当且仅当

$$<{\tilde{\mathbf{w}}}_k,{\mathbf{w}}_l>={\delta }_{kl}=\{\begin{array}{l}0,k\ne l\\ 1,k=l\end{array}$$
时， 它们才是双规范正交基。

令$W=\left\{{\mathbf{w}}_0,{\mathbf{w}}_1,{\mathbf{w}}_2,\cdots \right\}$是内积空间$V$的一个正交基，并且令$z\in V$，则向量$z$可 表示为基向量的线性组合：
$$\mathbf{z}={\alpha }_0{\mathbf{w}}_0+{\alpha }_1{\mathbf{w}}_1+{\alpha }_2{\mathbf{w}}_2+\cdots$$

计算得：
$${\alpha }_i=\frac{⟨{\mathbf{w}}_i,\mathbf{z}⟩}{⟨{\mathbf{w}}_i,{\mathbf{w}}_i⟩}$$
若基向量的范数为1， 则简化为：${\alpha }_i=<{\mathbf{w}}_i,\mathbf{z}>$

二、基于矩阵的变换

一维离散傅里叶变换是一类重要的变换， 这类变换可用如下通式表示：
$$T(u)=\sum _{x=0}^{N-1}f(x)r(x,u)\text{\hspace{1em}(16)}$$
其中， $x$是空间变量；$T(u)$是$f(x)$的变换；$r(x,u)$是正变换核；整数$u$是变换变量， 其值域为$0,1,2,\cdots ,N-1$。

$T(u)$的反变换：
$$f(x)=\sum _{u=0}^{N-1}T(u)s(x,u)\text{\hspace{1em}(17)}$$
其中， $s(x,u)$是反变换核， x的值域为$0,1,2,\cdots ,N-1$。$f(x)$是N个反变换核的加权和， $T(u)$是权重。
展开式$(17)$右侧得到：
$$f(x)=T(0)s(x,0)+T(1)s(x,1)+\cdots +T(N-1)s(x,N-1)\text{\hspace{1em}(18)}$$

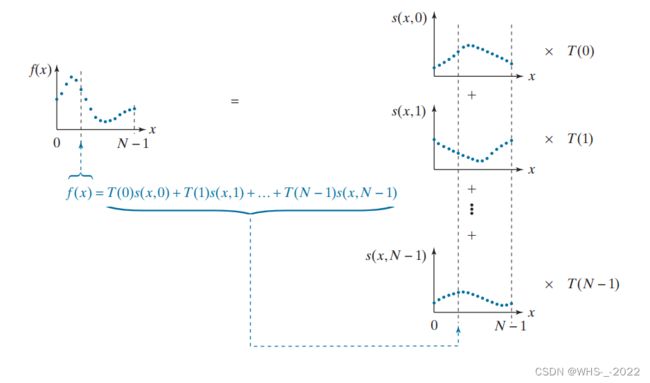
假设式$(17)$中的s(x, u)是内积空间的正交基向量，且基向量的范数为1，则：
$$T(u)=⟨s(x,u),f(x)⟩\text{\hspace{1em}(19)}$$

即变换的每个元素$T(u)$， 可通过内积来计算。

现在准备利用矩阵来表达式$(16)$和式$(17)$。首先将函数$f(x)$，$T(u)$和$s(x,u)$定义为列向量：
$$\mathbf{f}={\left[\begin{array}{ll}f(0)& f(1)\cdots f(N-1)\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{lll}{f}_0& f_1\cdots & f_{N-1}\end{array}\right]}^{\mathrm{T}}\text{\hspace{1em}(20)}$$
$$\mathbf{t}={\left[\begin{array}{ll}T(0)& T(1)\cdots T(N-1)\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{lll}{t}_0& t_1\cdots & t_{N-1}\end{array}\right]}^{\mathrm{T}}\text{\hspace{1em}(21)}$$

$$s_u=[s(0,u)s(1,u)\cdots s(N-1,u){]}^{\mathrm{T}}={\left[s_{u,0}{s}_{u,1}\cdots s_{u,N-1}\right]}^{\mathrm{T}}$$

其中，$u=0,1,\cdots ,N-1$
利用这些列向量， 重写式$(19)$， 得：
$$T(u)=<s_u,f>,u=0,1,\cdots ,N-1\text{\hspace{1em}(23)}$$

A = [ s 0 T s 1 T ⋮ s N − 1 T ] = [ s 0 s 1 … s N − 1 ] T (24) \mathbf{A}=\left[\begin{array}{c} \mathbf{s}_{0}^{T} \\ \mathbf{s}_{1}^{T} \\ \vdots \\ \mathbf{s}_{N-1}^{T} \end{array}\right]=\left[\begin{array}{llll} \mathbf{s}_{0} & \mathbf{s}_{1} & \ldots & \mathbf{s}_{N-1} \end{array}\right]^{T}\tag{24} A= ​s0T​s1T​⋮sN−1T​​ ​=[s0​​s1​​…​sN−1​​]T(24)

然后将式$(23)$代入式$(21)$， 并利用式$(1)$， 得
A A T = [ s 0 T s 1 T ⋮ s N − 1 T ] [ s 0 s 1 … s N − 1 ] = [ s 0 T s 0 s 0 T s 1 … s 0 T s N − 1 s 1 T s 0 s 1 T s 1 ⋮ ⋮ ⋱ s N − 1 T s 0 … s N − 1 T s N − 1 ] = [ ⟨ s 0 , s 0 ⟩ ⟨ s 0 , s 1 ⟩ … ⟨ s 0 , s N − 1 ⟩ ⟨ s 1 , s 0 ⟩ ⟨ s 1 , s 1 ⟩ ⋮ ⋮ ⋱ ⟨ s N − 1 , s 0 ⟩ … ⟨ s N − 1 , s N − 1 ⟩ ] = [ 1 0 … 0 0 1 ⋮ ⋮ ⋱ 0 … 1 ] = I (27) \begin{aligned} \mathbf{A A}^{T} & =\left[\begin{array}{c} \mathbf{s}_{0}^{T} \\ \mathbf{s}_{1}^{T} \\ \vdots \\ \mathbf{s}_{N-1}^{T} \end{array}\right]\left[\begin{array}{llll} \mathbf{s}_{0} & \mathbf{s}_{1} & \ldots & \mathbf{s}_{N-1} \end{array}\right] \\ & =\left[\begin{array}{cccc} \mathbf{s}_{0}^{T} \mathbf{s}_{0} & \mathbf{s}_{0}^{T} \mathbf{s}_{1} & \ldots & \mathbf{s}_{0}^{T} \mathbf{s}_{N-1} \\ \mathbf{s}_{1}^{T} \mathbf{s}_{0} & \mathbf{s}_{1}^{T} \mathbf{s}_{1} & & \vdots \\ \vdots & & \ddots & \\ \mathbf{s}_{N-1}^{T} \mathbf{s}_{0} & \ldots & & \mathbf{s}_{N-1}^{T} \mathbf{s}_{N-1} \end{array}\right] \\ & =\left[\begin{array}{cccc} \left\langle\mathbf{s}_{0}, \mathbf{s}_{0}\right\rangle & \left\langle\mathbf{s}_{0}, \mathbf{s}_{1}\right\rangle & \ldots & \left\langle\mathbf{s}_{0}, \mathbf{s}_{N-1}\right\rangle \\ \left\langle\mathbf{s}_{1}, \mathbf{s}_{0}\right\rangle & \left\langle\mathbf{s}_{1}, \mathbf{s}_{1}\right\rangle & & \vdots \\ \vdots & & \ddots & \\ \left\langle\mathbf{s}_{N-1}, \mathbf{s}_{0}\right\rangle & \ldots & & \left\langle\mathbf{s}_{N-1}, \mathbf{s}_{N-1}\right\rangle \end{array}\right] \\ & =\left[\begin{array}{cccc} 1 & 0 & \ldots & 0 \\ 0 & 1 & & \vdots \\ \vdots & & \ddots & \\ 0 & \ldots & & 1 \end{array}\right]=\mathbf{I} \end{aligned}\tag{27} AAT​= ​s0T​s1T​⋮sN−1T​​ ​[s0​​s1​​…​sN−1​​]= ​s0T​s0​s1T​s0​⋮sN−1T​s0​​s0T​s1​s1T​s1​…​…⋱​s0T​sN−1​⋮sN−1T​sN−1​​ ​= ​⟨s0​,s0​⟩⟨s1​,s0​⟩⋮⟨sN−1​,s0​⟩​⟨s0​,s1​⟩⟨s1​,s1​⟩…​…⋱​⟨s0​,sN−1​⟩⋮⟨sN−1​,sN−1​⟩​ ​= ​10⋮0​01…​…⋱​0⋮1​ ​=I​(27)

或
$$t=Af\text{\hspace{1em}(26)}$$
对于一维信号， 利用矩阵表达式$(16)$和式$(17)$为
$$t=Af\text{\hspace{1em}(28)}$$
$$f=A^{T}t\text{\hspace{1em}(29)}$$
式$(28)$和式$(29)$是可逆变换对。

本节中给出的大部分概念， 可推广到形如下式的连续展开：
$$f(x)=\sum _{u=-\infty }^{+\infty }{\alpha }_u{s}_u(x)\text{\hspace{1em}(51)}$$
其中， ${\alpha }_u$和$s_u$，$u=0,\pm 1,\pm 2,\pm 3,\cdots$分别表示内积空间$C([a,b])$的展开系数和基向量。

若$s_u$，$u=0,\pm 1,\pm 2,\pm 3,\cdots$是$C([a,b])$的正交基向量， 则展开系数：
$${\alpha }_u=⟨s_u(x),f(x)⟩\text{\hspace{1em}(52)}$$

三、相关

本节介绍这些系数与相关之间的关系。