【从零开始的机器学习】-06 多元线性回归问题
导语
我们在【从零开始的机器学习】-05 线性代数基础中介绍了一些线性代数的基础,包括矩阵的一些运算和操作。在本章,我们将运用这些操作,实现多元线性回归问题的参数最优化和预测。
1. 什么是多元线性回归问题?
在之前的章节里,我们以“用房屋面积来预测房价”为例,介绍了一元线性回归问题。其中,自变量(也被称为特征值)只有“房屋面积”这一个,而因变量则是“房价”。然而,在更为一般的问题中,自变量往往不不止一个,比如我们在预测房价时,不仅需要考虑房屋的面积,还会考虑房间的个数,楼层数,建筑年龄等因素。此时,因为自变量不再是一个,而是多个,因此问题从一元线性回归问题,变成了多元线性回归问题。
2. 多元线性回归模型表达式
所谓线性,根据数学的定义,
- 定义1:一个函数h(x)是只拥有一个自变量的一阶多项式函数,表达式为 h ( x ) = k x + b h(x) = kx+b h(x)=kx+b,k和b为常数,则称h(x)为线性函数
- 定义2:若有 h ( x + y ) = h ( x ) + h ( y ) h(x+y)=h(x)+h(y) h(x+y)=h(x)+h(y)成立,则称h(x+y)为线性函数。
- 更为"啰嗦"的定义:若h(x)可以拆成多个满足定义1的线性函数的和,则称h(x)为线性函数
多元线性回归的表达式:
h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + ⋯ + θ n x n h(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+\dots+\theta_nx_n h(x)=θ0+θ1x1+θ2x2+θ3x3+⋯+θnxn
如果我们用矩阵表示的话:设 参数向量 θ = [ θ 0 θ 1 θ 2 ⋮ θ n ] \theta = \left[ \begin{matrix} \theta_0\\ \theta_1\\ \theta_2\\ \vdots\\ \theta_n \end{matrix}\right] θ=⎣⎢⎢⎢⎢⎢⎡θ0θ1θ2⋮θn⎦⎥⎥⎥⎥⎥⎤,自变量向量 x = [ 1 x 1 x 2 ⋮ x n ] x = \left[ \begin{matrix} 1\\ x_1\\ x_2\\ \vdots\\ x_n \end{matrix}\right] x=⎣⎢⎢⎢⎢⎢⎡1x1x2⋮xn⎦⎥⎥⎥⎥⎥⎤, h ( x ) = θ T x h(x)=\theta^{T}x h(x)=θTx, θ \theta θ是一个 1 × ( n + 1 ) 1\times(n+1) 1×(n+1)的向量, x x x是 ( n + 1 ) × 1 (n+1)\times 1 (n+1)×1的向量,二者相乘,就是 h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + ⋯ + θ n x n h(x)=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+\dots+\theta_nx_n h(x)=θ0+θ1x1+θ2x2+θ3x3+⋯+θnxn
3. 代价函数与梯度下降法
3-1 代价函数
现在我们已经知道多元线性回归的表达式了,该确定评价标准(代价函数)了。我们继续采用平方误差函数计算。如果我们用朴素的(非矩阵表达)方式描述代价函数的话,相比于一元线性回归,多项式的代价函数会稍微复杂一些,但因为我们使用了矩阵,因此看起来并没有很大的区别:
J ( θ 0 , θ 1 , … , θ n ) = ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 2 m = ∑ i = 1 m ( ∑ j = 1 n θ j x j ( i ) − y ( i ) ) 2 2 m — — ( 变 体 1 ) = ∑ i = 1 m ( θ T x − y ( i ) ) 2 2 m — — ( 变 体 2 ) J(\theta_0,\theta_1, \dots, \theta_n)=\frac{\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^{2}}{2m}\\\;\\ =\frac{\sum_{i=1}^{m}(\sum_{j=1}^{n}\theta_{j}x_{j}^{(i)}-y^{(i)})^{2}}{2m}\;\;\;\;\;\;\;——(变体1)\\\;\\ =\frac{\sum_{i=1}^{m}(\theta^{T}x-y^{(i)})^{2}}{2m}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;——(变体2) J(θ0,θ1,…,θn)=2m∑i=1m(hθ(x(i))−y(i))2=2m∑i=1m(∑j=1nθjxj(i)−y(i))2——(变体1)=2m∑i=1m(θTx−y(i))2——(变体2)
3-2 梯度下降法
为了实现梯度下降法,我们需要求代价函数 J ( θ 0 , θ 1 , … , θ n ) J(\theta_0,\theta_1, \dots, \theta_n) J(θ0,θ1,…,θn)对于 θ 0 , θ 1 , … , θ n \theta_0,\theta_1,\dots,\theta_n θ0,θ1,…,θn的偏导数来描述各参数在某个位置的变化趋势。和一元线性方程的解法一致,都是固定一个自变量,其他自变量当成常数系数,然后求导。
关于 θ 0 \theta_0 θ0的偏导数: ∂ J ( θ 0 , θ 1 , … , θ n ) ∂ θ 0 = ∑ i = 1 m ( θ T x − y ( i ) ) m \frac{\partial J(\theta_0,\theta_1, \dots, \theta_n)}{\partial \theta_0}=\frac{\sum_{i=1}^{m}(\theta^{T}x-y^{(i)})}{m} ∂θ0∂J(θ0,θ1,…,θn)=m∑i=1m(θTx−y(i))
关于 θ j ( j = 1 , 2 , … , n ) \theta_j (j=1,2,\dots,n) θj(j=1,2,…,n)的偏导数: ∂ J ( θ 0 , θ 1 , … , θ n ) ∂ θ j = ∑ i = 1 m ( θ T x − y ( i ) ) x j ( i ) m \frac{\partial J(\theta_0,\theta_1, \dots, \theta_n)}{\partial \theta_j}=\frac{\sum_{i=1}^{m}(\theta^{T}x-y^{(i)})x^{(i)}_{j}}{m} ∂θj∂J(θ0,θ1,…,θn)=m∑i=1m(θTx−y(i))xj(i)
根据上面的偏导数,我们可以构建梯度下降法的函数表达式,学习率为α:
θ 0 : = θ 0 − α ∂ J ( θ 0 , θ 1 , … , θ n ) ∂ θ 0 = θ 0 − α ∑ i = 1 m ( θ T x − y ( i ) ) m \theta_0 := \theta_0-\alpha \frac{\partial J(\theta_0,\theta_1, \dots, \theta_n)}{\partial \theta_0} = \theta_0-\alpha \frac{\sum_{i=1}^{m}(\theta^{T}x-y^{(i)})}{m} θ0:=θ0−α∂θ0∂J(θ0,θ1,…,θn)=θ0−αm∑i=1m(θTx−y(i))
θ j : = θ j − α ∂ J ( θ 0 , θ 1 , … , θ n ) ∂ θ 0 = θ j − α ∑ i = 1 m ( θ T x − y ( i ) ) x j ( i ) m \theta_j := \theta_j-\alpha \frac{\partial J(\theta_0,\theta_1, \dots, \theta_n)}{\partial \theta_0} = \theta_{j} - \alpha \frac{\sum_{i=1}^{m}(\theta^{T}x-y^{(i)})x^{(i)}_{j}}{m} θj:=θj−α∂θ0∂J(θ0,θ1,…,θn)=θj−αm∑i=1m(θTx−y(i))xj(i)
与一元线性回归问题相同,参数需要同步更新。
import numpy as np
import random
def h_true(x1,x2,x3,x4,x5) -> int: #用于生成测试数据的函数
return 1+x1+2*x2+3*x3+4*x4+5*x5
def cost_function(data,theta)->float: #代价函数
m = data.shape[0] #数据量
n = data.shape[1] #特征量
x = data[:,0:n-1] #1+自变量
y = data[:,n-1] #真实值
base = x.dot(theta)-y #h(x)-y
return sum(base.T.dot(base))/(2*m)
def gradient_decrase_multi(x,y,m,n,theta,alpha)->[]: #梯度下降法
#计算每个偏导数的公共部分,即:h(x) - y, 得到一个1000x1的矩阵
base = x.dot(theta)-y
# print(base.shape)
#计算每个特征量的偏导数,因为特征量j的偏导数=m行的 base值乘以第i行的第j列的值的和
#根据矩阵的计算方法,base.T是1x1000的矩阵,乘以第j列的每一项,然后相加
#将base转置成1x1000的矩阵,然后和矩阵x相乘,就可以得到每个特征量的偏导数结果,得到一个1x6的矩阵
partial = base.T.dot(x)
# print(partial.shape)
#将偏导数矩阵转置成6x1的矩阵,乘以学习率,然后用原本的theta减去得到的结果,就可以完成同步更新,得到一个6x1的矩阵
theta = theta-alpha*(partial.T)
# print(theta.shape)
return theta
if __name__ == '__main__':
data = []
for i in range(0,1000):
x1 = random.randrange(-100,100,1)
x2 = random.randrange(-100, 100, 2)
x3 = random.randrange(-100, 100, 3)
x4 = random.randrange(-100, 100, 4)
x5 = random.randrange(-100, 100, 5)
data.append([1,x1,x2,x3,x4,x5,h_true(x1,x2,x3,x4,x5)]) #第i行输入x的向量的转置
data = np.mat(data)
theta = [[100],[-100],[100],[-100],[100],[-100]]
theta = np.mat(theta)
ans = cost_function(data,theta)
mylogs = []
m = data.shape[0]
n = data.shape[1]
x = data[:, 0:n - 1]
y = data[:, n - 1]
for i in range(0,10000):
theta = gradient_decrase_multi(x,y,m,n,theta,0.0000005)
if(i>9990):
mylogs.append(cost_function(data,theta).item(0,0))
print(theta)
print(mylogs)
4. 特征缩放(Feature Scaling)
如果我们保证所有的特征值在相似的范围内,可以使梯度下降法更快收敛(因为梯度下降法在小范围内下降的很快,在大范围内下降的很慢。这个范围最后相对统一,且不会太大或者太小,比如-1 ~ 1,-3 ~ 3,0 ~ 3,都是可以接受的。但是想-100~100,10000~20000就太大了,而像0.00001~0.00002这样的又太小。
缩放的方法:
- 用该特征值下的每一个值都除以该特征的所有数据中最大值和最小值的差,就可以保证数据再一个相对小的范围了
- 均值归一化(mean normalization):每个数据都减去该特征值的数据平均值,以此获得一个平均值为0的数据集(除了x0,不要用x0去减平均值,x0是我们为了方便计算,添加进矩阵的,而非特征值)
- 将上面的两个方法结合,先减去平均值,在除以最大值和最小值的差,或者除以标准差,进行缩放:
x i : = x i − u i m a x ( x ) − m i n ( x ) 或 x i − u i S D ( x ) x_{i}:=\frac{x_{i}-u_{i}}{max(x)-min(x)}\;或\;\frac{x_{i}-u_{i}}{SD(x)} xi:=max(x)−min(x)xi−ui或SD(x)xi−ui
需要注意的是,如果我们对训练集进行了缩放,那么对测试数据也要用相同的方法进行缩放,否则无法得到正确的预测值(这一点非常容易被忘记)
代码实现:
import numpy as np
import random
def h_true(x1,x2,x3,x4,x5) -> int: #用于生成测试数据的函数
return 1+x1+2*x2+3*x3+4*x4+5*x5
def cost_function(data,theta)->float: #代价函数
m = data.shape[0] #数据量
n = data.shape[1] #特征量
x = data[:,0:n-1] #1+自变量
y = data[:,n-1] #真实值
base = x.dot(theta)-y #h(x)-y
return sum(base.T.dot(base))/(2*m)
def gradient_decrase_multi(x,y,m,n,theta,alpha)->[]: #梯度下降法
#计算每个偏导数的公共部分,即:h(x) - y, 得到一个1000x1的矩阵
base = x.dot(theta)-y
# print(base.shape)
#计算每个特征量的偏导数,因为特征量j的偏导数=m行的 base值乘以第i行的第j列的值的和
#根据矩阵的计算方法,base.T是1x1000的矩阵,乘以第j列的每一项,然后相加
#将base转置成1x1000的矩阵,然后和矩阵x相乘,就可以得到每个特征量的偏导数结果,得到一个1x6的矩阵
partial = base.T.dot(x)
# print(partial.shape)
#将偏导数矩阵转置成6x1的矩阵,乘以学习率,然后用原本的theta减去得到的结果,就可以完成同步更新,得到一个6x1的矩阵
theta = theta-alpha*(partial.T)
# print(theta.shape)
return theta
if __name__ == '__main__':
data = []
for i in range(0,10):
x1 = random.randrange(-100,100,1)
x2 = random.randrange(-100, 100, 2)
x3 = random.randrange(-100, 100, 3)
x4 = random.randrange(-100, 100, 4)
x5 = random.randrange(-100, 100, 5)
data.append([1,x1,x2,x3,x4,x5,h_true(x1,x2,x3,x4,x5)]) #第i行输入x的向量的转置
data = np.mat(data,dtype='float32')
theta = [[0],[0],[0],[0],[0],[-0]]
theta = np.mat(theta)
ans = cost_function(data,theta)
mylogs = []
m = data.shape[0]
n = data.shape[1]
x = data[:, 0:n - 1]
y = data[:, n - 1]
mean = [0]
diff = [1]
# 特征缩放
for i in range(1,6):
temp = data[:,i]
mean.append(np.mean(temp)) #平均值
diff.append((max(temp)-min(temp)).item(0,0)) #最大和最小值的差值
data[:,i] = (temp-mean[i])/diff[i] #缩放
mean = np.mat(mean,dtype="float32")
diff = np.mat(diff,dtype="float32")
for i in range(0,10000):
theta = gradient_decrase_multi(x,y,m,n,theta,0.01)
if(i>9990):
mylogs.append(cost_function(data,theta).item(0,0))
print(theta)
print(mylogs)
结果为:
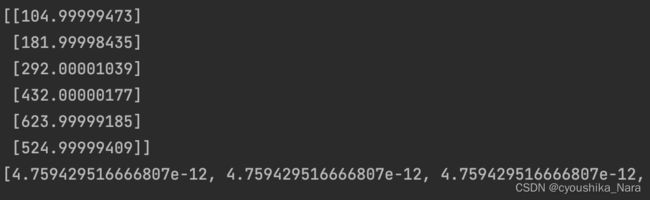
我们发现,怎么 θ \theta θ这么大?难道不应该是[1,2,3,4,5]吗?这是因为,我们仅对x进行了缩放,但是没有对y进行缩放(我们也不能对真实值进行缩放,否则会失真)。用缩放后的x得到原来的y,参数自然和不缩放时的参数不同了。重要的是代价,我们发现代价已经是10^-12次方级的了,可与默认为0,因此 θ \theta θ是正确的。同时,我们发现如果不缩放,我们的学习率必须设的很小,比如0.00000005才能正确地学习,而进行缩放之后,我们用0.01作为学习率就可以了。
5. 如何对梯度下降法Debug?
当特征量超过2个时,我们无法通过绘制图像的方法观察模型的样子。作为替代,我们可以观察迭代步数和代价之间的关系变化。
我们每次下降迭代时,都计算一下当前参数下的代价为多少。然后以迭代步数为横坐标,代价值为纵坐标,绘制曲线,观察变化趋势,调整学习率和迭代次数
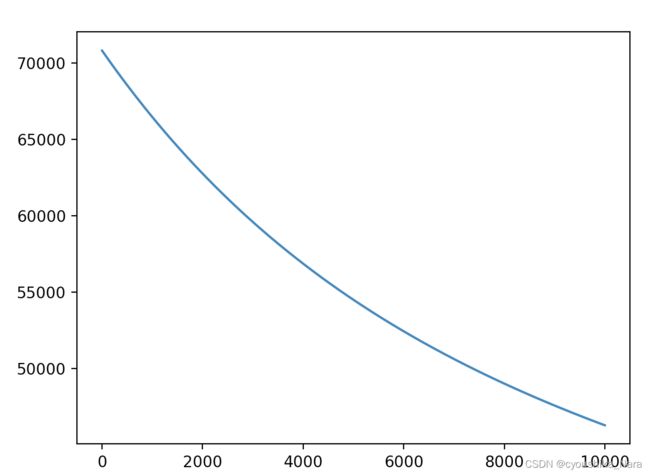
5-1 学习率太低(0.00001):曲线过于平缓,且还在下降,没有到达收敛值
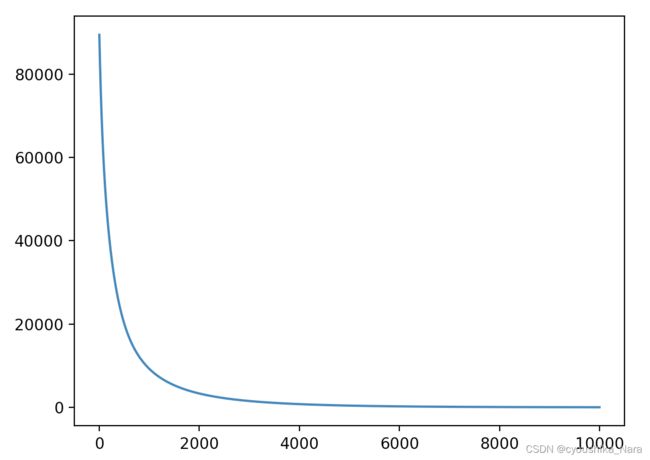
5-2 合适的学习率(0.01):末尾趋于平稳,说明学习率合适
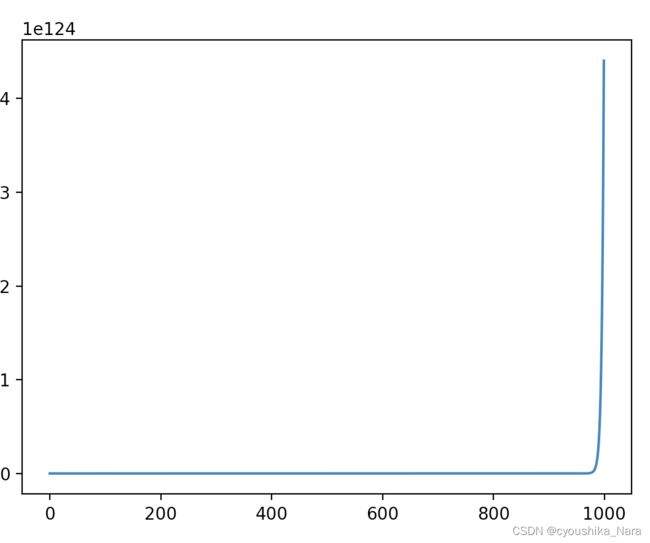
学习率过大(0.215):代价不降反升,或者呈波浪上下变动时,说明梯度下降法是失灵的,需要更小的学习速率
6. 正规方程求解最优参数(Normal Equation)
除了梯度下降法,还有一种方法可以求解最优参数,那就是正规方程(Normal Equation)。正规方程如下:
θ = ( X T X ) − 1 X T y \theta = (X^TX)^{-1}X^Ty θ=(XTX)−1XTy
上面方程是可以通过数学证明的,但证明的部分不在本系列的范围内,故省略。
X为 m × ( n + 1 ) m\times(n+1) m×(n+1)的矩阵,y为 m × 1 m\times1 m×1的向量。正规方程不需要特征缩放,也不需要学习率,更不需要迭代,而是直接一步就计算出最优参数。但是,根据公式,我们需要计算 X T X X^TX XTX的逆矩阵,而 X T X X^TX XTX如果是奇异矩阵,则不存在逆矩阵,因而也无法用正规方程求解。
出现不可逆的原因:
- 特征冗余:比如有两个特征,一个是房子的面积,用英制单位,另一个也是房子的面积,用公制单位,由于英制和公制之间存在转换关系,所以两个特征实际上是同一个特征
- 特征太多,训练集太少(即m<=n)
应对方法:
- 删除一些特征
- 正规化(之后的章节里会讲)
代码实现:
import numpy as np
import random
def h_true(x1,x2,x3,x4,x5) -> int: #用于生成测试数据的函数
return 1+x1+2*x2+3*x3+4*x4+5*x5
def normal_equation(x,y):
return (x.T.dot(x)).I.dot(x.T).dot(y)
if __name__ == '__main__':
data = []
for i in range(0, 10):
x1 = random.randrange(-100, 100, 1)
x2 = random.randrange(-100, 100, 2)
x3 = random.randrange(-100, 100, 3)
x4 = random.randrange(-100, 100, 4)
x5 = random.randrange(-100, 100, 5)
data.append([1, x1, x2, x3, x4, x5, h_true(x1, x2, x3, x4, x5)]) # 第i行输入x的向量的转置
data = np.mat(data, dtype='float32')
m = data.shape[0]
n = data.shape[1]
x = data[:, 0:n - 1]
y = data[:, n - 1]
theta = normal_equation(x,y)
print(theta)
7. 梯度下降法 vs 正规方程
| 项目 | 梯度下降法 | 正规方程 |
|---|---|---|
| 学习率 | 需要设置 | 不需要设置 |
| 迭代 | 需要迭代 | 不需要迭代 |
| 大量特征 | 能够很好的运行 | 会变的很慢 (O(n^3)) |
| 奇异矩阵 | 无影响 | 会出现错误,无法执行 |
对于线性回归问题,当特征量在1~10000之内时,可以考虑用正规方程,但是超过10000个特征,就需要考虑用梯度下降法。
8. 模型改进(特征融合)
有时我们会发现线性的函数模型未必能很好的拟合数据,这个时候我们需要对模型进行调整,比如引入其他一些曲线模型,调整特征的指数(融合一些特征,比如房屋的长和宽,我们可以融合成面积)等。
比如,我们假设函数为 h ( x ) = θ 0 + θ 1 × x 1 h(x)=\theta_0+\theta_1\times x_1 h(x)=θ0+θ1×x1,然后我们基于x1,设 x 2 = x 1 2 x_2 = x_1^2 x2=x12,设计一个二次函数:
h ( x ) = θ 0 + θ 1 × x 1 + θ 2 × x 1 2 h(x) = \theta_0+\theta_1\times x_1+\theta_2\times x_1^2 h(x)=θ0+θ1×x1+θ2×x12
或者我们基于x1,设 x 2 = x 1 2 , x 3 = x 1 3 x_2 = x_1^2, x_3 = x_1^3 x2=x12,x3=x13,设计一个三次函数:
h ( x ) = θ 0 + θ 1 × x 1 + θ 2 × x 1 2 + θ 3 × x 1 3 h(x) = \theta_0+\theta_1\times x_1+\theta_2\times x_1^2+\theta_3\times x_1^3 h(x)=θ0+θ1×x1+θ2×x12+θ3×x13
这样操作,有时会比线性模型更好地拟合数据。需要注意的是,如果采用上面的方法改变函数模型,特征值的值域也会变化,因此需要用到缩放,假设x1的值域为1~ 1000,那么x2的范围就是1 ~ 10^6,需要进行100万的缩放,而x3的范围是1 ~ 10^9次方,因此需要进行10^9的缩放。
9. 预告
回归问题我们已经讨论的差不多了,接下来我们将进入分类问题的部分。