Gables: A Roofline Model for Mobile SoCs

为了帮助构建 SoC 思维并指导早期移动 SoC 设计，Gables: A Roofline Model for Mobile SoCs 提出了 Gables 模型，该模型改进和重新定位了 Roofline 模型（最初为多核芯片的性能和带宽限制而设计）来对 SoC 上的每个加速器进行建模，在不同的加速器之间并发的分配工作（由文中用例分析证明），并计算 SoC 性能上限。作者使用现有 SoC （Snapdragon 835）评估 Gables 模型并开发了多个扩展，使 Gables 能够为早期移动 SoC 设计提供信息。

I. INTRODUCTION

处理器架构不断从单核微处理器发展到多核芯片，再到复杂的片上系统（SoC）。最后一次转型既是技术推动，也是应用拉动。这一推动是 Dennard Scaling 的结束和摩尔定律的减缓，促进在某些计算中使用比 CPU 核心更节能的加速器。这种拉动是应用趋向于“特殊用途”和无处不在的计算，从视频处理到深度神经网络处理。

大多数现代智能手机都包含先进的 SoC 体系结构，这些体系结构由多核、GPS 和许多不同的可编程和固定功能加速器组成，这些加速器通过复杂的互连层次结构连接，目标是在严格的功率、热和能量限制下运行十几个或更多关键软件用例。现代 SoC 不断增长的复杂性对硬件计算机架构师如何最好地进行早期构思提出了挑战。一旦指定了硬件并编写或移植了加速器软件，后期 SoC 设计通常依赖于详细的全系统仿真。然而，早期的 SoC 设计通常必须在编写一行软件之前选择加速器。

虽然 SoC 中的 IP 多样性和异构性为系统集成商（即将 SoC 集成到手机中的公司）提供了大量的替代方案，但也给他们带来了一些独特的挑战：

• 一方面，SoC 设计人员很难确定哪些架构设计功能最有可能在未来的 SoC 中有用——这必须提前三年完成；
• 另一方面，最终用户（即应用程序设计人员）需要评估不同 SoC 之间的几种不同权衡，以确定哪种 SoC 最适合其性能、功耗和成本目标。

解决其中任何一个挑战都不容易。没有行业标准的方法来表征、评估和比较移动 SoC。当今应用最广泛的 SoC 性能评估工具是基于后硅基准测试，使用 Geekbench 和 AnTuTu 等工具，没有达到预期效果。这些基准测试主要关注 CPU 和内存子系统，大多忽略了 SoC 的其他组件。因此，它们无法表征 SoC 丰富的异构能力。此外，现有的基准测试工具面向硅后测量和测试，而不是硅前探索。设计、创建和选择计算机系统需要有原则性的方法，消费级移动 SoC 也不例外。计算机体系结构中的主要模式是使用时钟级仿真，我们期望在 SoC 设计的后期继续这样做。然而，SoC 设计的早期阶段存在诸如“我的 SoC 应包含哪些 IP 以及大致有多大？”之类的问题。此外，SoC客户还面临着一个挑战，即在可供选择的具有不同大小的不同 IP 的已设计 SoC 中进行向下选择。

由于替代品之间“移植” SoC 工作负载的巨大开销，对早期问题使用时钟级仿真是不实际的。今天，消费者 SoC 必须支持10到20个重要的“用例”——比如打电话或看电影——都能很好地运行。平均值无关紧要。在替代设计之间改变当前用例既昂贵又耗时，因为针对不同的 IP 更接近于重写代码而不是“移植”。此外，在 SoC 部署到产品中以及软件可能未完全编写完成之前，必须提前2到3年规划未来用例。由于时钟级仿真无法用于早期决策，因此可以求助于直觉、一些 SoC 参数，或者——正如我们所提倡的——使用 SoC 和工作负载用例参数来驱动模型。

为了促进早期 SoC 设计或选择，我们重新调整了 Roofline 性能模型的用途。Roofline 将瓶颈分析[Quantitative System Performance] 应用于处理器芯片，最初是多核芯片。它使用峰值计算性能（$P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$）和峰值片外内存带宽（$B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$）对芯片硬件进行建模，并使用操作强度（$I$）对软件进行建模，操作强度（$I$）是片外传输到内存或从内存传输片外的每个字节的平均操作数（例如，浮点）。操作强度提醒我们，数据重用对于管理带宽使用至关重要。在不重复使用的情况下，双精度乘法累加的操作强度可低至 $0.063=\frac{1}{16}=\frac{2operations}{4\ast 8bytes}$。图 1 给出了最大可达到的对数性能（$y$ 轴）图，其上限为带宽（斜线）或峰值性能（水平线），具体取决于 软件的对数操作强度（$x$ 轴）。由于限制，屋顶线图可以添加作为较低边界的天花板。

Roofline 模型尚未应用于消费类 SoC。挑战的一部分是定义具有许多不同加速器的 SoC 的整体峰值性能，而不是单个同质多核芯片。出于这个原因，我们转而将 Roofline 应用于单个 SoC 加速器，并认为此种方法最为合适。然后，我们提出了 Gables SoC 模型，这是 Roofline 瓶颈分析的推广。在其基本形式中，Gables 针对 N 个 IP 块（例如 CPU 组和加速器）的 SoC，这些 IP 块可以彼此并行运行并进行内存传输。Gables 借助每个 IP 的屋顶线，以及它们的共享内存带宽需求方程为 SoC 硬件建模。Gables 使用每个 IP 的作业百分比（如 Amdahl 定律）和操作强度对工作负载用例进行建模，然后可以计算用例在 SoC 上可达到的最大性能。我们使用现代 SoC 上的微观基准来评估 Gables。我们提供了基础 Gables 模型的扩展，这些扩展本身是有价值的，并说明许多其他扩展是可能的。我们为内存端内存、暂存器、缓存和互连拓扑以及在 IP 之间串行工作的用例开发扩展。此外，我们提供了一个开源 Gables 移动应用程序和一个交互式可视化工具，以促进更深入的理解[10]。

II. MOBILE SOC BACKGROUND

A. SoC Architecture

图 3 显示了典型现代 SoC 的示例框图。不出所料，它由一个 CPU（AP）和 GPU 集群复合体组成。大多数现代智能手机依赖于非对称处理，大的乱序核心处理面向用户和计算要求高的任务，而小的有序核心处理后台处理任务，例如检查电子邮件和触发通知。许多 SoC 仅包含大和小 CPU，但最近，联发科 Helio X30 引入了新的“中间”级，仅在 CPU 复合体中就形成了三个层次的异构性。

除了 CPU 和 GPU，移动 SoC 中还有大量其他处理引擎。事实上，移动 CPU 组仅占总芯片面积的25%到30%[4]、[3]，其余部分都分给了这些专用处理引擎。图 3 包括一些来说明这一点。简而言之，其中许多 IP 负责在计算密集型场景下执行繁重的工作。

IP 成功的关键在于，与 CPU 相比，它们以相对较低的功耗提供了巨大的马力。例如，谷歌在 Pixel 3智能手机上推出的 Pixel Visual Core（IPU）[13]旨在加速相机应用中的高动态范围( HDR )处理。HDR 是一项计算密集型任务，用于扩展亮度范围，而不是使用标准图像处理技术可能实现的任务。IPU 是一个8核处理器（本身），每个核心每秒可以执行3万亿次操作，使其在 HDR+处理速度上比主应用处理器快5倍，功率只有主应用处理器的十分之一。同样，Qualcomm Hexagon 数字信号处理器 (DSP) 是机器学习智能和计算机视觉的引擎（比 CPU 快8倍，比 GPU 快4倍），其能效分别比 CPU 和 GPU 高出近8倍和25倍[14]。

许多（如果不是所有的话）硬件 IP 都聚集到一个分层网络结构中。在图 3 中，我们展示了多个网络结构，每个结构都有其速度和馈源。根据 IP 的带宽和延迟要求，将 IP 聚集到不同的结构层次结构级别中。

B. Usecases

SoC 世界中的应用程序通常被称为“用例”。这些应用用例图是传感器到处理引擎的最佳应用级数据流。图 4 显示了通过 WiFi 流式传输互联网内容的示例用例。此场景的一般用例流程如下：通过 WiFi 流式传输的 IP 数据包被处理到用户/应用程序级缓冲区中，进入不安全的内存。音频和视频流被分离，由加密块（或 CPU）解密，并存储在安全内存中。视频解码器和音频流都会缓冲一些播放秒数，以解决网络延迟问题。音频 DSP（例如 Qualcomm 的 Hexagon DSP）发起直接内存访问（Direct Memory Access, DMA） 传输到其 SRAM，视频解码器读取视频流并开始在内存中生成将由显示控制器使用的帧缓冲区。音频流在到达音频 DSP 之前都是编码的。CPU 只有在传输数据时才显示。它可能有控制流特性，而在该图中没有显示。

在移动 SoC 中，典型的用例数据流同时运行多个 IP。表 I 显示了五种不同的用例以及 SoC 中常用的不同 IP 的集合。为了篇幅，我们只展示了五个用例。五个用例都对应于相机应用程序。相机应用程序是智能手机中使用最频繁的应用程序之一，它依赖严格的实时性能保证来维持。否则，用户的体验可能会受到影响。因此，我们在这里详细讨论。在表 I 中的所有相机用例中，至少有一半的 IP 同时处于活动状态。因此，用例的性能主要由芯片内部进行的所有并发活动决定。这与阿姆达尔定律形成鲜明对比，后者在不同 IP 上的工作是串行的。

用例的性能在很大程度上取决于三个基本方面：

• 首先是单个 IP 的计算性能，它受执行引擎的隔离能力以及支持该引擎的 IP 内部存储器层次结构和互连的影响。如果 IP 的整体性能不足以在整体处理速度上保持稳定的流，那么并发应用程序数据流的任何部分都可能成为瓶颈。
• 第二个是 IP 与外部的数据移动。尤其是相机应用程序，在高帧率 (HFR) 下会消耗大量内存带宽。让我们以每秒240帧（FPS）的“4K”视频录制为例。一幅4K 图像每帧3840x2160个像素。假设使用 YUV420颜色编码系统，每4个像素使用6个字节，帧大小大约为12MB。以高帧率处理如此大的图像，数据在不同 IP 之间移动，例如用于小波降噪（WNR）和时间降噪（TNR）的图像信号处理器（ISP），同时通过 DRAM 跟踪多达5个参考帧，可能导致移动 SoC 的内存带宽（大约30GB/s）成为瓶颈。
• 第三个主要的用例瓶颈是 IP 之间的协调开销，如今总体上;是通过 CPU 路由的。由于 IP 对外而言是单独的设备（至少在 Android 中），所以每当 IP 完成处理时，CPU 都会显式中断。CPU 必须处理向该数据的消费者发送启动信号的任务。

对于所有 SoC 集成商来说，了解上述哪些原因会导致系统出现瓶颈都是一项具有挑战性的任务。因此，使用早期工具来指导 SoC 的整体架构是非常有益的。

III. GABLES: AMULTI-IP ROOFLINE MODEL

从整体上表征和理解包含多种加速器的移动 SoC 性能，其关键挑战在于很难深入了解整个 SoC 的性能。在 CPU 和 GPU 系统中，可以通过隔离特定 IP 来研究系统和在该系统上运行的应用程序的特性，而移动 SoC 的性能及其用例是多个 IP 间并发活动的结果。因此，我们方法的目标是设计一个可以为 SoC 提供直觉和洞察力的模型，就像 Roofline 为多核芯片所做的那样，Amdahl 定律为一般并行系统所做的那样。

在本节中，我们将介绍 Gables SoC 性能模型，其中硬件对每个 IP 都有一个 Roofline，并且工作负载用例将工作分配到不同 IP。该模型可用于确定移动 SoC 中性能的临界限制，并可通过单个图上的多个屋顶线进行可视化。尽管我们特别关注处于极端异构计算前沿的移动系统，但该模型可推广应用于任意 SoC 设计。

A. SoC Model and High-level Assumptions

Gables 以图 5 所示的 SoC 为目标，这是典型的现代 SoC，具有 $N$ 个 IP 块 $\mathrm{I}\mathrm{P}[i]，i=0，N-1$，一个外部 DRAM 存储器的接口，以及高带宽的片上互连。为便于参考，表 II 提供了本节将介绍的所有 Gables 参数。

Gables 模型的基线做了几个硬件假设：

• 首先，每个 $\mathrm{I}\mathrm{P}[i]$ 都有一个由其峰值性能和 IP 进出带宽定义的屋顶线；
• 其次，SoC 上的所有 IP 都同时运行（如第 II-B 节所述）并共享片外存储器带宽；
• 第三，片上互连具有足够的带宽，可以仅通过从 IP 和片外存储器连接到它的带宽来建模；
• 第四，所有大数据量的 IP 间通信都通过 DRAM 内存进行，在该内存中可以进行数兆字节的缓冲/速率匹配。

基本模型还做了软件用例假设：

• 首先，根据第 II-B 节的用例观察，将用例划分为每个 $\mathrm{I}\mathrm{P}[i]$ 上的并发非负工作；
• 其次，用例在每个 IP 上的操作强度可能不同，因为工作的各个方面被分配给不同的 IP 和（或）IP 具有不同的内部缓存或暂存器，例如，为了减少延迟而不是容许时延；
• 第三，我们假设该软件同时使用多个 IP，这也是我们之前在第 II-B 节中提出并在表 I 中总结的基本原理。

B. Two-IP Model: A Primer

我们首先介绍具有双 IP SoC 的 Gables，因为它在概念上更简单，并且所有概念都扩展到了 N-IP SoC。例如，双 IP SoC 可能将 $\mathrm{I}\mathrm{P}[0]$ 作为 CPU（应用处理器）组，将 $\mathrm{I}\mathrm{P}[1]$ 作为 GPU。令 SoC 的最大片外内存带宽为 $B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$。

Gables 模型假设两个 IP 都有一个由硬件定义的屋顶线和一个由用例选择的操作点。$\mathrm{I}\mathrm{P}[0]$ 硬件具有峰值计算性能 $P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$ 和进出带宽 $B_0$。$\mathrm{I}\mathrm{P}[1]$ 硬件具有峰值计算性能 $A\cdot P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$，其中 $A$ 是其加速度，以及进出带宽 $B_1$。给定的用例会将操作强度为 $I_0$ 的 $(1-f)$ 工作分配给 $\mathrm{I}\mathrm{P}[0]$，将操作强度为 $I_1$ 的 $f$ 工作分配给 $\mathrm{I}\mathrm{P}[1]$，其中 $0\le f\le 1$。从广义上讲，这遵循阿姆达尔定律，但工作是并行进行的，而不是顺序进行的。

运行时间

Gables 假设 SoC 完成用例的时间可能受到 $\mathrm{I}\mathrm{P}[0]$、$\mathrm{I}\mathrm{P}[1]$ 或 DRAM 内存接口的时间限制：

• 首先，$\mathrm{I}\mathrm{P}[0]$ 的计算时间是它的工作量除以其峰值性能：$C_0=(1-f)/P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$。$\mathrm{I}\mathrm{P}[0]$ 做这项工作需要的数据容量（字节）是该工作量除以其操作强度：$D_0=(1-f)/I_0$。传输 $\mathrm{I}\mathrm{P}[0]$ 所需数据的最短时间是该数据容量除以 $\mathrm{I}\mathrm{P}[0]$ 到互连的带宽：$D_0/B_0$。最后，$\mathrm{I}\mathrm{P}[0]$ 执行用例的最短时间是其数据传输和计算时间的最大值：
  $$T_{\mathrm{I}\mathrm{P}[0]}=\max (\frac{D_0}{B_0},C_0)$$

• 其次，$\mathrm{I}\mathrm{P}[1]$ 的方程遵循类似的模式，尽管峰值性能 $A\cdot P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$、IP 带宽 $B_1$、工作量 $f$ 和操作强度 $I_1$ 等输入略有不同，从而产生 $C_1=f/(A\cdot P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}})$，$D_1=f/I_1$ 和：
  $$T_{\mathrm{I}\mathrm{P}[1]}=\max (\frac{D_1}{B_1},C_1)$$

• 第三，在芯片内外传输数据的最短时间是要传输的总数据除以内存带宽：
  $$T_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{y}}=\frac{D_0+D_1}{B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}}$$

• 第四，SoC可达到的最大性能与每个组件的最大时间成反比：
  $$P_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}}=\frac{1}{\max (T_{\mathrm{I}\mathrm{P}[0]},T_{\mathrm{I}\mathrm{P}[1]},T_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{y}})}$$

性能/Roofline

或者，通过代数和再展开项，当 $0<f<1$ 时，下列性能方程提供上述时间方程的对偶：
$$\frac{1}{T_{\mathrm{I}\mathrm{P}[0]}}=\frac{\min (B_0\cdot I_0,P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}})}{(1-f)}$$
$$\frac{1}{T_{\mathrm{I}\mathrm{P}[1]}}=\frac{\min (B_1\cdot I_1,A\cdot P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}})}{(f)}$$
$$\frac{1}{T_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{y}}}=B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}\cdot I_{\mathrm{a}\mathrm{v}\mathrm{g}}$$
其中 $I_{\mathrm{a}\mathrm{v}\mathrm{g}}=1/((1-f)/I_0)+(f/I_1))$ 是 $I_0$ 和 $I_1$ 的调和平均值，按每个 IP 的工作量百分数加权。

请注意：

• 等式 5 和 6 只是通过除以工作量的百分数来缩放的 IP 屋顶线；
• 等式 7 是内存屋顶线的倾斜部分；
• 等式 8 选择最小的屋顶线。

这些性能方程的缺点是，在处理所有 $0\le f\le 1$ 时，如果 $f=0$，则必须删除 $\mathrm{I}\mathrm{P}[0]$ 项，如果 f = 1，则必须删除 $\mathrm{I}\mathrm{P}[1]$ 项，以避免出现除以零的异常。它们关键优势在于支持我们接下来开发的多屋顶线可视化。

C. Visualizing Gables via Scaled Rooflines

在这里，我们为 Gables 开发了多屋顶线图：

• 沿用 Roofline 的坐标轴（x 轴为对数级操作强度 $I$ 和 y 轴为对数级可达到性能 $P_{\mathrm{a}\mathrm{t}\mathrm{t}}$）；
• 通过改变 x 轴上的操作强度来显示方程 5-7 中的3条缩放屋顶线；
• 在操作强度 $I_0$、$I_1$ 和 $I_{\mathrm{a}\mathrm{v}\mathrm{g}}$ 处添加"垂直线"选定每个屋顶线上的性能；
• 根据公式 8，将可达到的性能显示为屋顶线中选定的最低点。

图 6 展示了双 IP Gable 的示例序列，其中我们的示例假定 $\mathrm{I}\mathrm{P}[0]$ 是一个 CPU 组，其缓存支持数据重用，而 $\mathrm{I}\mathrm{P}[1]$ 是一个 GPU，设计用于延迟容忍，而不是带宽减少。我们从硬件输入开始， $P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}=40$ Gops/s、$B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}=10$ Gbytes/s、$A_1=5$、$B_0=6$ 和 $B_1=15$。对于软件用例，我们假设在 $\mathrm{I}\mathrm{P}[0]$ 上 $I_0=8$，$\mathrm{I}\mathrm{P}[1]$ 的 $I_1=0.1$，$f=0$。如图 6a 所示，$I_0$ 将性能限制为 40 Gops/s，内存为 80 Gops/s，而 $\mathrm{I}\mathrm{P}[1]$ 未显示，因为没有分配任何工作给它（$f=0$）。整体性能为40 Gops/s，相当于 $\mathrm{I}\mathrm{P}[0]$ 的较差性能，令人失望，因为未使用的 $\mathrm{I}\mathrm{P}[1]$ 可以达到200 Gops/s。

图 6b 所示的显著变化是通过设置 $f=0.75$ 将工作分配给 $\mathrm{I}\mathrm{P}[1]$ 来寻求更高的性能。然而，性能下降到1.3 Gops/s（四舍五入为1）。为什么？答案是我们分配的内存带宽不足，因为 $\mathrm{I}\mathrm{P}[1]$（$I_1=0.1$）的数据重用率低，这使得 $\mathrm{I}\mathrm{P}[1]$ 和内存屋顶线在最左侧的操作强度接近 0.1 处提供了边界。

如果内存带宽有问题，也许将 $B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$ 从 10 GB/s 增加到 30 GB/s 是有意义的，结果如图 6c 所示。这将性能从1.3提高到2 Gops/s，但这仍然令人失望。此外，它将内存顶线移动到了其他两个边界之上，产生了额外的开销而没有好处（对于本用例）。

图 6d 显示了我们的最终 SoC，有两个变化：

• 首先，我们通过向 $\mathrm{I}\mathrm{P}[1]$ 增加内存（寄存器/暂存器/缓存）并确保用例重用来其中的数据（说起来容易做起来难），将 $I_1$ 从0.1增加到8（如 $\mathrm{I}\mathrm{P}[0]$）。
• 其次，我们将 $B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$ 从30降低到足够的20 Gops/s。

这导致总体性能为160 Gops/s，所有三条屋顶线在 $I=8$ 时相等，这是一个完美平衡的设计。

此示例显示了双 IP Gables 的一些(教学)值。就 CPU 而言，GPU 可以用任何其他加速器代替，同样的结论也成立。但 Gables 的全部功能有待于处理更复杂的 N-IP SOC，我们将在下一步开发。

D. Multi-IP Model

在这里，我们将双 IP 模型推广到具有 $N$ 个不同 $\mathrm{I}\mathrm{P}[i]，i=0，N-1$ 的 SoC，如图 5 所示。SoC 仍具有峰值计算性能为 $P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$ 的 $\mathrm{I}\mathrm{P}[0]$ 和 $B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$ 的片外内存带宽。每个 $\mathrm{I}\mathrm{P}[i]$ 具有性能 $A_i\cdot P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$ 和带宽 $B_i$ ，并且 $A_0=1$。用例将操作强度为 $I_i$ 的并发工作 $f_i$ 分配给 $\mathrm{I}\mathrm{P}[i]$，其中 $f_i$ 为非负数，并且总和为1。在每个 $\mathrm{I}\mathrm{P}[i]$，计算时间 $C_i=f_i/(A_i\cdot P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}})$，传输数据量 $D_i=f_i/I_i$，最短时间：
$$T_{\mathrm{I}\mathrm{P}[i]}=\max (\frac{D_i}{B_i},C_i)$$

内存接口的最短时间是传输的总数据量除以内存带宽：
$$T_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{y}}=\frac{{\sum }_{i=0}^{N-1}{D}_i}{B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}}$$

用例在 N-IP Soc 上可达到的最大性能是：
$$P_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}}=\frac{1}{\max (T_{\mathrm{I}\mathrm{P}[0]},\dots ,T_{\mathrm{I}\mathrm{P}[N-1]},T_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{y}})}$$

当 $f_i=0$ 时，对偶性能/屋顶线方程同样忽略 $\mathrm{I}\mathrm{P}[i]$ 项，并使用加权谐波平均值 $I_{\mathrm{a}\mathrm{v}\mathrm{g}}=1/({\sum }_{i=0}^{N-1}{f}_i/I_i$。
$$\frac{1}{T_{\mathrm{I}\mathrm{P}[i]}}=\frac{\min (B_i\cdot I_i,A_i\cdot P_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}})}{f_i}$$
$$\frac{1}{T_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{y}}}=B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}\cdot I_{\mathrm{a}\mathrm{v}\mathrm{g}}$$
$$T_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{y}}=\min (\dots ,\frac{1}{T_{\mathrm{I}\mathrm{P}[i]}},\dots ,\frac{1}{T_{\mathrm{m}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{y}}})$$

上述方程完成了基础的 Gables 模型，但可以进行扩展和变化（第 V 节）。

幸运的是，双 IP Gables 图还可以推广到可视化 N 个 IP，每个 IP 使用一个缩放的屋顶线加上一个内存屋顶线。有关双 IP 和三个 IP SoC 的交互式可视化，以及 Gables 开源 Android 应用程序的线索，请参见 Gables 主页。

IV. EXPERIMENTAL EVALUATION

为了探索 Gables SoC 屋顶线模型是否提供洞察力，我们使用它来实证检验现有的商用现成的消费智能手机 SoC。黑盒芯片或 IP 的确切屋顶线很难准确确定。对屋顶线的乐观估计是使用制造商的规格(如果有的话)。这些可能通过功能单元的速度乘以数量，得到一个不能超过但可能无法达到的数字。或者，对屋顶线的悲观估计使用不同的微基准来寻求最佳的可实现性能。这些估计得出的屋顶线是可以达到的，但可能不是最佳性能（即，可能是天花板）。在本节中，我们使用后一种经验方法（即上限）来查看 Gables 是否提供了有关 SoC 的洞察力，即使没有挖掘出最终峰值性能。

A. Methods

我们确定了移动 SoC 中三种最常见的通用计算引擎的屋顶线：CPU、GPU 和 DSP。目标是评估 Gables 模型估定真实硬件行为的准确度。随着参数的变化，Gables 的性能预测至少应具有正确的形状和合理的相对误差。然而，Gables 将高质量绝对精度（但几乎永远无法实现）的目标留给了执行用例软件的周期级模拟。

我们对两款商用 Qualcomm SoC 进行评估，即 Snapdragon 835 和 Snapdragon 821。 我们在这些移动 SoC 上对三个最可编程的引擎进行了实验：CPU、GPU 和 DSP。我们的研究结果对这两个系统都适用，因此在这里我们只讨论两种芯片组中最新的芯片组（即高通 Snapdragon 835）的结果。

Snapdragon 835 包括 Qualcomm Kryo CPU、Adreno 540 GPU、Hexagon 682 数字信号处理器（Digital Signal Processor，DSP），以及其他一些特定领域的加速器，例如调制解调器和音频（视频)编码器。CPU有八个核心（高达1.9GHz）。GPU 专注于图形（OpenGL、DX12），具有有限的通用支持，号称在略高于700 MHz 的频率下，最大性能为 540 GFLOPS/s。DSP 利用具有四个线程的专用标量处理器处理非常宽（1024 位）的整数向量，支持有限的单精度 (SP)，并且它可以在 920 MHz 的时钟频率下进行峰值操作。

算法 1 演示了我们在每个 IP 上运行的微基准测试。其基本思想是让所有 IP 处理元素加载特定大小数组中的每个字，并对其执行一定数量的操作。我们改变数组大小以查看不同内存占用下的性能变化。我们修改每个字的操作数以控制操作强度，并在不同的 IP 上重复对这个内核进行基准测试，以确定系统的带宽（GB/s）和计算限制（GFLOPS/s）。这个计算内核的结构最初是由 Empirical Roofline Toolkit 的作者构想的。

默认情况下，我们在算法中假设的字长是 32 位，运算是单精度浮点乘法。单精度是科学计算历来首选的双精度与新兴算法（例如机器学习推理）偏爱的半精度（或更低）之间的折衷。所有三个引擎（CPU、GPU 和 DSP）都支持 IEEE 兼容的单精度，因此它们具有可比性。要真正实现峰值性能，应充分利用计算引擎的 SIMD 能力，我们将在后面讨论。

B. CPU and GPU Rooflines

正如我们在第 III-C 节中所做的那样，我们从双 IP 开始探索：CPU（$\mathrm{I}\mathrm{P}[0]$）和 GPU（$\mathrm{I}\mathrm{P}[1]$）。图 7a 显示了我们根据经验得出的 CPU $\mathrm{I}\mathrm{P}[0]$ 屋顶线估计值。峰值性能为 7.5 GFLOPS/s，可视为较低。我们没有运行 NEON（SIMD）指令集优化的微基准。当我们在编译器支持的情况下对代码应用向量化时，我们可以实现超过40 GFLOP/s 的峰值（未显示）。只要我们与一个基准保持一致，我们使用的确切基准不会影响我们以后的分析。自此，我们仅参考非 NEON 峰值性能。DRAM 的带宽为15.1 GB/s，仅为峰值的50%。公布的理论峰值带宽为30 GB/s。带宽较低，部分原因是我们在算法 1 中同时执行读写操作。我们将此作为分析的基础，因为这在实用程序中比只读访问更常见。作为健全性检查，我们还运行了一个只读版本的微基准测试（未显示）其速度接近20 GB/s，并且与由来已久的基准 STREAM 和 lmbench 一致。

仅从这个测试，无法判断带宽是否受到来自 IP（$B_0$）、片外带宽（$B_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}$）或其他实体（例如互连）的限制。通过使用更小的微基准数组大小，CPU 可以从其内部 L1和 L2缓存获得更高的带宽。

图 7b 显示了我们根据经验得出的 Adreno GPU $\mathrm{I}\mathrm{P}[1]$ 的屋顶线估计。对于 GPU，由于它通常更多地是主要用于渲染图形的流式工作负载，而不是通用计算，因此我们应用了内核的轻微变体。我们从一个数组执行流读取并更新另一个数组，就像在 CPU STREAM 内核中一样，这使得 GPU 能够最大化其读取带宽和计算能力；这种场景在 GPU 应用程序中比 CPU 应用程序更为典型。

Adreno 540的理论峰值性能为567 GFLOPS。我们能够获得的峰值性能是349.6 GFLOPS/s。这使我们能够估计其相对于CPU的加速度为 $A_1=349.6/7.5=46.6\approx 47X$。当启用积极的 SIMD 优化时，这个 $47X$ 减少到一个数量级以下，这与先前的结论一致[23]。正如人们所预料的那样，峰值 DRAM 带宽更高，为24 GB/s。GPU 并行运行1024个工作组，每个工作组有256个线程。

C. Gables for Two IPs

在本节中，我们根据 Gables 的工作量分数和操作强度假设，在 Snapdragon 芯片的 CPU 和 GPU 上运行我们的微基准测试，进行实证检查以表明 Gables 提供了一些见解。

图 8 显示了结果。$y$ 轴以操作强度为 $I_0=1$ 的所有工作分配到 CPU $\mathrm{I}\mathrm{P}[0]$ 上（$f=0$）的性能为基准。$x$ 以1/8的增量显示 GPU 上的工作量分数 $f$ 从0（所有工作在 CPU）到1。所有运行都执行相同的总工作量（单精度操作数），当 $0<f<1$ 时，IP 并行运行。不同的行显示不同的操作强度，从每字节1到1024个操作。

从数据中很难得出绝对的结论，但我们可以观察到一些总体趋势：

• 首先，我们发现当操作强度较低时，将工作从 CPU 卸载到 GPU 会导致性能下降（除了一个与图 6b 中糟糕的性能一样糟糕）。这一结果表明，不应将低操作强度的工作卸载到 GPU。
• 其次，当操作强度很高时，将工作从 CPU 卸载到更快的 GPU 会产生较大的加速比，例如 $I_0=I_1=1024$ 时为 39.4。

因此，加速可以发挥作用（这并不奇怪），但要了解的重要一点是，我们可以通过硬件加速器实现的优势很大程度上取决于固有的工作负载特征，这不仅包括被卸载的工作量占比 还有被卸载的那部分的操作强度。

D. Toward N-IP SoC

作为将 Gables 应用于两个以上 IP 的一步，我们还为 Hexagon DSP 构建了屋顶线，并像上一节一样继续进行“混合”分析。可以将 Hexagon DSP 视为具有两个组件：

• 设计为（几乎）始终开启的低功耗标量单元；
• 高性能整数向量单元（每周期4096位）。

我们选择关注标量单元，因为它可以执行微基准测试的单精度浮点操作，并允许我们进行比较和对比。

图 9 显示了 Hexagon DSP 标量单元的屋顶线。我们在算法 1 上获得了3.0 GFLOPS/s 的性能，略低于规范预测的四个线程最大 3.6 GFLOPS/s。虽然相对于 CPU 的加速度较低，但标量 DSP 提供了低功耗卸载的价值，加速度由矢量单位决定。DSP 的带宽限制在12.5GB / s，远小于 CPU 和 GPU，很可能是由于采用了不同的互连结构，如图 3 所示的通用 SoC。

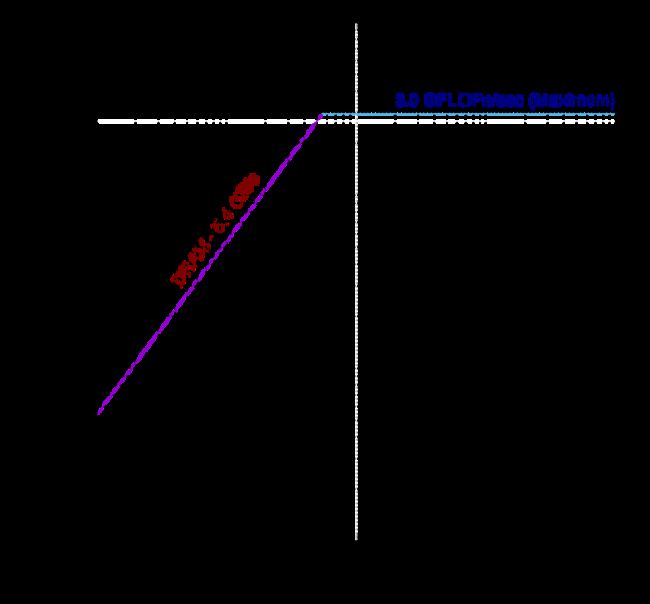
我们通过让 DSP 标量单元与 CPU 和 GPU 并行工作来执行一些“混合”分析。我们在这里没有显示结果，因为标量 DSP 太弱了，无法实质性地干扰 CPU-GPU 的行为。我们将使用 DSP 向量单元进行检查，但这将需要改变方法，因为 DSP 仅对整数向量进行操作。

VII. SUMMARY AND CONJECTURES

本文最后给出了关于Gables的猜想，这些猜想似乎是正确的，但需要进一步的工作才能稳健地确立：

• 在时钟级仿真可行之前，Gables 等 SoC 模型对 SoC 设计和选型具有重要价值。随着计算机体系结构行业越来越倾向于设计加速器以提供未来性能，我们将看到开发系统方法来在早期阶段以相对较少的参数理解平衡设计和加速器选择的强烈需求。随后的猜想讨论了 Gables 具体参数的取值。

• 确定单个 SoC IP 的上限是有价值的，即它们的加速能力 $A_i$ 和带宽 $B_{[i]}$ 。例如，我们发现，这让我们以比预期更多的努力深入了解 Snapdragon 芯片，但比移植完整用例的投入要少得多。

• 对于重要用例，估计每个 IP 的工作量占比 $f_i$ 至关重要。这样做可以说明 IP 是否过度设计，提供了超出分配给它的工作所需的加速能力（$A_i$）。又是阿姆达尔定律。

• 操作强度 $I_i$ 需要仔细考虑，因为数据重用对于减少所需的带宽至关重要。高操作强度需要从软硬件两方面考虑：

  • 在 IP 中提供足够的寄存器、暂存器或缓存
  • 更改算法以很好地使用本地内存

  操作强度也可以说明缺陷，例如添加更多 IP 本地内存，即使重要用例没有/不能使用增加的容量来增加重用（例如，当下一次重用机会需要更大的本地内存时）。

参考资料：

• Gables: A Roofline Model for Mobile SoCs
• Roofline Model Toolkit: A Practical Tool for Architectural and Program Analysis
• berkeleylab/cs-roofline-toolkit
• Applying the Roofline Model
• Mansard Roofline Model: Reinforcing the Accuracy of the Roofs
• AMAIX: A Generic Analytical Model for Deep Learning Accelerators
• Applying the Roofline Model for Deep Learning performance optimizations
• harvard-edge/Gables
• Amdahl’s Law(阿姆达尔定律)
• CPU Complex (CCX) - AMD
• 锐龙AMD Ryzen 7处理器——核心探秘
• 系统架构（一）
• Pixel Visual Core: A closer look at Google’s hidden chip
• 如何看待谷歌第一块移动芯片Pixel Visual Core？
• CUDA Handbook 补充 CPU和GPU硬件架构2
• 28种缓存替换策略的分类整理｜《Cache Replacement Policies》Chapter 2