Kaggle时间序列(Time Series)教程 3-季节性(Seasonality)

什么是季节性？

只要序列的平均值有规律的、周期性的变化，我们就说时间序列表现出季节性。 季节性变化通常遵循时钟和日历——一般一天、一周或一年的重复。 季节性通常是由自然界在几天和几年内的循环或围绕的日期和时间的社会行为惯例驱动的。

四个时间序列中的季节性。

我们将学习两种关于季节性的特征。 第一种，指示器(indicators)，最适合一个季节性周期中有少量的观察值，例如在每天的观察值中找到以周为周期的季节性。 第二种，傅里叶特征(Fourier features)，最适合一个季节性周期中有许多的观察值，例如在每天的观察值中找到以年为周期的季节性。

季节性图(Seasonal Plots)和季节性指示器(Seasonal Indicators)

就像我们使用移动平均图来发现系列中的趋势一样，我们可以使用季节性图来发现季节性。

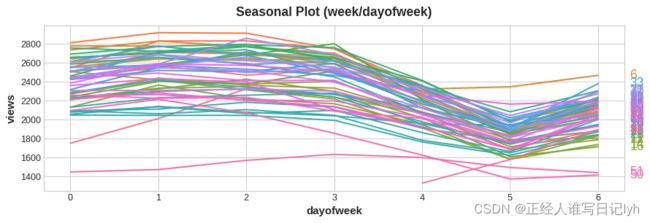
季节性图显示了针对某个常见时期绘制的时间序列片段，该时期是您要观察的“季节”。 该图显示了维基百科关于 三角学(Trigonometry) 的文章的每日浏览量的季节性图：文章的每日浏览量是在一个共同的 每周 期间绘制的。

该系列有明显的以周为周期季节性，工作日较高，周末下降。

季节性指示器(Seasonal indicators)

季节性指示器是表示时间序列水平的季节性差异的二元特征(Seasonal indicators are binary features that represent seasonal differences in the level of a time series)。 如果您将季节性周期视为分类特征并进行独热编码，则可以得到季节性指示器。

通过对一周中的每一天进行独热编码，我们得到每周的季节性指示器。 为 三角学(Trigonometry) 系列创建每周每周的季节性指示器将为我们提供六个新的“虚拟”特征。
（如果删除其中一个指示器，线性回归效果会更好；所以我们在下表中选择删除了星期一。）

Date	Tuesday	Wednesday	Thursday	Friday	Saturday	Sunday
2016-01-04	0.0	0.0	0.0	0.0	0.0	0.0
2016-01-05	1.0	0.0	0.0	0.0	0.0	0.0
2016-01-06	0.0	1.0	0.0	0.0	0.0	0.0
2016-01-07	0.0	0.0	1.0	0.0	0.0	0.0
2016-01-08	0.0	0.0	0.0	1.0	0.0	0.0
2016-01-09	0.0	0.0	0.0	0.0	1.0	0.0
2016-01-10	0.0	0.0	0.0	0.0	0.0	1.0
2016-01-11	0.0	0.0	0.0	0.0	0.0	0.0
…	…	…	…	…	…	…

向训练数据中添加季节性指示器有助于模型识别季节性周期内的平均值：

普通线性回归学习季节中每个时间的平均值。

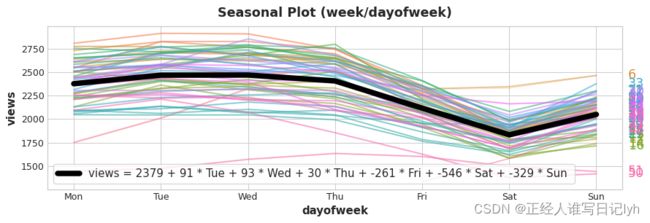
指示器就像一个开关一样。 在任何时候，这些指示器中最多有一个的值为“1”（开）。 线性回归给星期一学习到一个基准值为2379，然后根据当天哪个指示器是开对值进行调整；其余的指示器由于值是0,所以值不会被计算。

傅里叶特征(Fourier Features )和周期图

我们现在讨论的特征更适合有许多观察值的长季节周期，这种情况使用指示器就很不明智（回忆我们之前的以周为周期的指示器，一周七天就会多出来6个特征，如果观察值过多，就会多出很多特征！）。 傅立叶特征不是为每个日期创建一个特征，而是尝试用几个特征来捕捉季节性曲线的整体形状。

让我们看一下 三角学(Trigonometry) 中的年度季节图。 注意各种频率的重复：每年3次长的上下运动，每年52次的短周运动，也许还有其他。

三角学(Trigonometry)序列的年度季节性变化

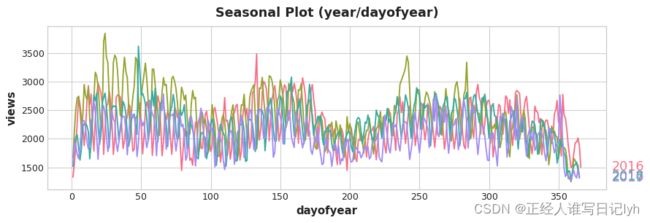
我们试图用傅里叶特征捕捉一个季节内的这些频率。 这个想法是在我们的训练数据中包含与我们试图建模的季节具有相同频率的周期性曲线。 我们使用的曲线是三角函数正弦和余弦的曲线。

傅里叶特征是成对的正弦和余弦曲线，从最长的季节开始，每个潜在频率都对应一对。 对年度季节性进行建模的傅立叶对将具有频率：每年一次、每年两次、每年三次，依此类推。

年度季节性的前两个傅立叶对。 上: 频率每年一次。 下: 频率每年两次。

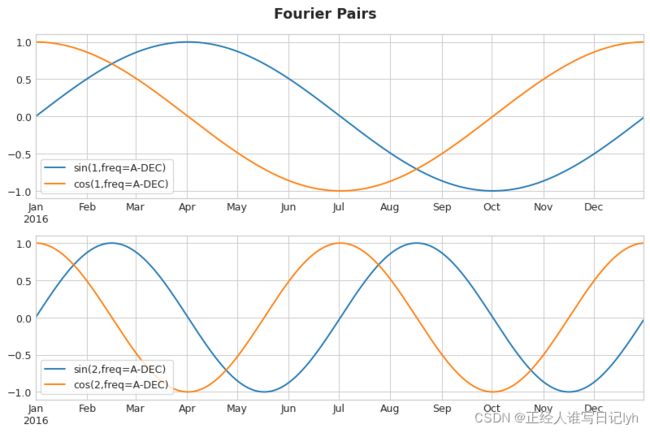
如果我们将一组这些正弦/余弦曲线添加到我们的训练数据中，线性回归算法将计算出适合目标序列中季节性分量的权重。 该图说明了线性回归如何使用四个傅立叶对来模拟 三角学(Trigonometry) 系列中的年度季节性。

上: 四个傅立叶对的曲线，正弦和余弦的总和以及回归系数。 每条曲线模拟不同的频率。 下: 这些曲线之和近似于季节性模式。

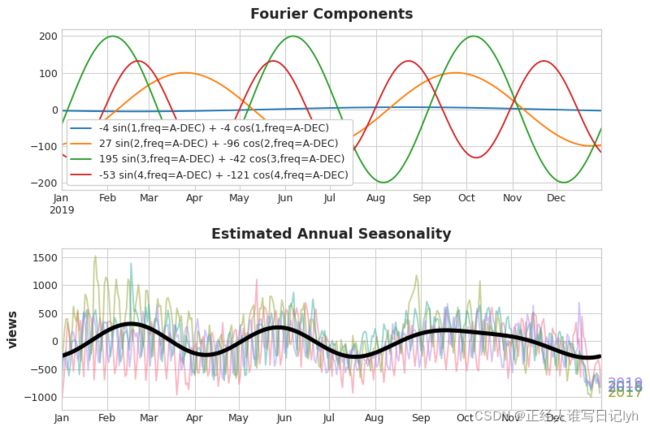
请注意，我们只需要八个特征（四个正弦/余弦对）就可以很好地估计年度季节性。 与需要数百个特征（一年中的每一天一个）的季节性指示器方法相比较。 通过仅使用傅立叶特征对季节性的“主效应”进行建模，向训练数据中添加特征更少，这意味着减少了计算时间并降低了过度拟合的风险。

使用周期图选择傅里叶特征

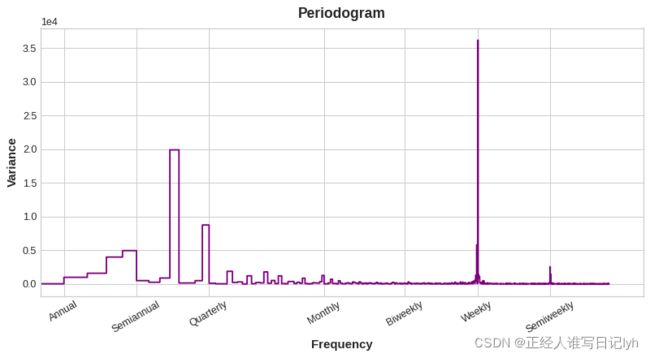
我们实际上应该在我们的特征集中包含多少傅里叶对呢？ 我们可以用周期图来回答这个问题。 周期图告诉您时间序列中频率的强度。 具体来说，图的 y 轴上的值为 (a ** 2 + b ** 2) / 2，其中 a 和 b 是该频率下正弦和余弦的系数（如 在上面的 Fourier Components 图中）。

*三角学(Trigonometry)*的周期图

从左到右，周期图在 Quarterly 之后下降，一年四次。 这就是我们选择四对傅立叶对来模拟年度季节的原因。 我们忽略了Weekly频率，因为它使用季节性指示器来建模更好。

计算傅里叶特征（可选）

了解傅里叶特征的计算方式对于使用它们并不是必不可少的，但如果看到细节可以更好的理解它，下面的单元格说明了如何从时间序列的索引中导出一组傅里叶特征。 （不过，我们将在应用程序中使用来自 statsmodels 的库函数。）

import numpy as np


def fourier_features(index, freq, order):
    time = np.arange(len(index), dtype=np.float32)
    k = 2 * np.pi * (1 / freq) * time
    features = {}
    for i in range(1, order + 1):
        features.update({
            f"sin_{freq}_{i}": np.sin(i * k),
            f"cos_{freq}_{i}": np.cos(i * k),
        })
    return pd.DataFrame(features, index=index)


# Compute Fourier features to the 4th order (8 new features) for a
# series y with daily observations and annual seasonality:
#
# fourier_features(y, freq=365.25, order=4)

示例 - Tunnel Traffic

我们将继续使用 Tunnel Traffic 数据集。 这个隐藏的单元格加载数据并定义了两个函数：seasonal_plot 和plot_periodogram。

from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.deterministic import CalendarFourier, DeterministicProcess

simplefilter("ignore")

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 5))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
    legend=False,
)
%config InlineBackend.figure_format = 'retina'


# annotations: https://stackoverflow.com/a/49238256/5769929
def seasonal_plot(X, y, period, freq, ax=None):
    if ax is None:
        _, ax = plt.subplots()
    palette = sns.color_palette("husl", n_colors=X[period].nunique(),)
    ax = sns.lineplot(
        x=freq,
        y=y,
        hue=period,
        data=X,
        ci=False,
        ax=ax,
        palette=palette,
        legend=False,
    )
    ax.set_title(f"Seasonal Plot ({period}/{freq})")
    for line, name in zip(ax.lines, X[period].unique()):
        y_ = line.get_ydata()[-1]
        ax.annotate(
            name,
            xy=(1, y_),
            xytext=(6, 0),
            color=line.get_color(),
            xycoords=ax.get_yaxis_transform(),
            textcoords="offset points",
            size=14,
            va="center",
        )
    return ax


def plot_periodogram(ts, detrend='linear', ax=None):
    from scipy.signal import periodogram
    fs = pd.Timedelta("1Y") / pd.Timedelta("1D")
    freqencies, spectrum = periodogram(
        ts,
        fs=fs,
        detrend=detrend,
        window="boxcar",
        scaling='spectrum',
    )
    if ax is None:
        _, ax = plt.subplots()
    ax.step(freqencies, spectrum, color="purple")
    ax.set_xscale("log")
    ax.set_xticks([1, 2, 4, 6, 12, 26, 52, 104])
    ax.set_xticklabels(
        [
            "Annual (1)",
            "Semiannual (2)",
            "Quarterly (4)",
            "Bimonthly (6)",
            "Monthly (12)",
            "Biweekly (26)",
            "Weekly (52)",
            "Semiweekly (104)",
        ],
        rotation=30,
    )
    ax.ticklabel_format(axis="y", style="sci", scilimits=(0, 0))
    ax.set_ylabel("Variance")
    ax.set_title("Periodogram")
    return ax


data_dir = Path("../input/ts-course-data")
tunnel = pd.read_csv(data_dir / "tunnel.csv", parse_dates=["Day"])
tunnel = tunnel.set_index("Day").to_period("D")

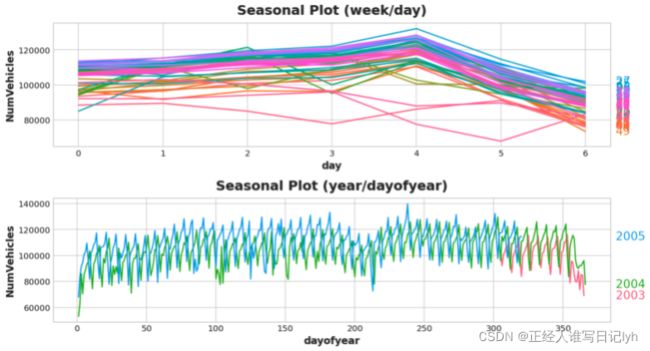
让我们来看看一周和一年的季节性图。

X = tunnel.copy()

# days within a week
X["day"] = X.index.dayofweek  # the x-axis (freq)
X["week"] = X.index.week  # the seasonal period (period)

# days within a year
X["dayofyear"] = X.index.dayofyear
X["year"] = X.index.year
fig, (ax0, ax1) = plt.subplots(2, 1, figsize=(11, 6))
seasonal_plot(X, y="NumVehicles", period="week", freq="day", ax=ax0)
seasonal_plot(X, y="NumVehicles", period="year", freq="dayofyear", ax=ax1);

现在让我们看一下周期图：

plot_periodogram(tunnel.NumVehicles);

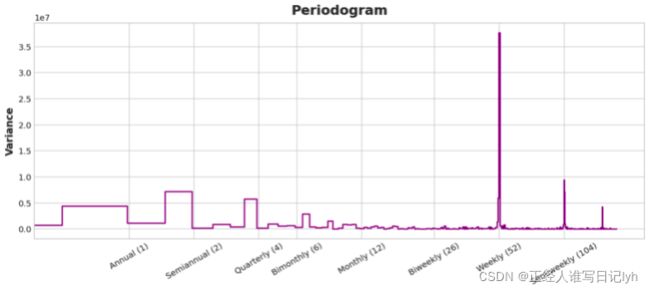
周期图与上面的季节图一致：每周季节性较强和每年季节性较弱。 我们将用指示器来对每周季节性进行建模，用傅里叶特征对每年的每年季节性。 从右到左，周期图在双月 (6) 和每月 (12) 之间递减，所以让我们使用 10 个傅立叶对。

我们将使用 DeterministicProcess 创建我们的季节性特征，我们在第 2 课中用于创建趋势(Trend)特征的相同方法。 要使用两个季节性时段（每周和每年），我们需要将其中一个实例化为“附加项”：

from statsmodels.tsa.deterministic import CalendarFourier, DeterministicProcess

fourier = CalendarFourier(freq="A", order=10)  # 10 sin/cos pairs for "A"nnual seasonality

dp = DeterministicProcess(
    index=tunnel.index,
    constant=True,               # dummy feature for bias (y-intercept)
    order=1,                     # trend (order 1 means linear)
    seasonal=True,               # weekly seasonality (indicators)
    additional_terms=[fourier],  # annual seasonality (fourier)
    drop=True,                   # drop terms to avoid collinearity
)

X = dp.in_sample()  # create features for dates in tunnel.index

创建特征集后，我们就可以拟合模型并进行预测了。 我们将添加一个 90 天的预测，以了解我们的模型如何在训练数据之外进行推断。 这里的代码与前面课程中的代码相同。

y = tunnel["NumVehicles"]

model = LinearRegression(fit_intercept=False)
_ = model.fit(X, y)

y_pred = pd.Series(model.predict(X), index=y.index)
X_fore = dp.out_of_sample(steps=90)
y_fore = pd.Series(model.predict(X_fore), index=X_fore.index)

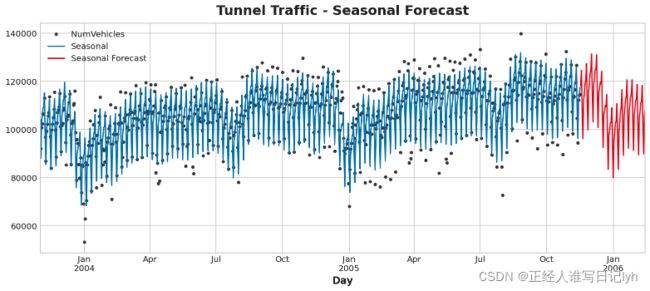
ax = y.plot(color='0.25', style='.', title="Tunnel Traffic - Seasonal Forecast")
ax = y_pred.plot(ax=ax, label="Seasonal")
ax = y_fore.plot(ax=ax, label="Seasonal Forecast", color='C3')
_ = ax.legend()

在时间序列上我们哈可以做更多的事情来改进我们的预测。 在下一课中，我们将学习如何将时间序列本身用作特征。 使用时间序列作为预测的输入可以让我们对序列中经常出现的另一个情况进行建模：周期。

轮到你了

为商店销售创建季节性特征 并将这些技术扩展到捕捉假日效果。