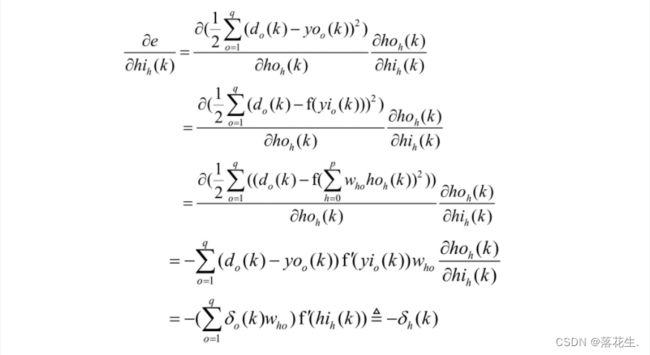数学建模算法与应用【BP神经网络算法】
评价预测和分类问题可以用到神经网络。卷积神经网络适合大样本的情况,深度学习包括很多种网络,如卷积神经网络,对抗网络等,深度学习大小样本皆可。
人工神经网络ANN
在机器学习和认知科学领域,人工神经网络 (artificial neural network缩写ANN),简称神经网络 (neuralnetwork,缩写NN) 或类神经网络,是一种模仿生物神经网络(动物的中枢神经系统,特别是大脑)的结构和功能的数学模型或计算模型,用于对函数进行估计或近似。
ANN能干什么?
神经网络的主要研究内容
•神经元模型
•激活函数
•网络结构
•工作状态
•学习方式
典型的神经网络具有以下三个部分:
1、结构 (Architecture) 结构指定了网络中的变量和它们的拓扑关系。例如,神经网络中的变量可以是神经元连接的权重 (weights) 和神经元的激励值 (activities of the neurons)
2、激励函数 (Activity Rule) 大部分神经网络模型具有一个短时间尺度的动力学规则,来定义神经元如何根据其他神经元的活动来改变自己的激励值。一般激励函数依赖于网络中的权重 (即该网络的参数)。
3、学习规则 (Learning Rule) 学习规则指定了网络中的权重如何随着时间推进而调整。这一般被看做是一种长时间尺度的动力学规则。一般情况下学习规则依赖于神经元的激励值。它也可能依赖于监督者提供的目标值和当前权重的值。
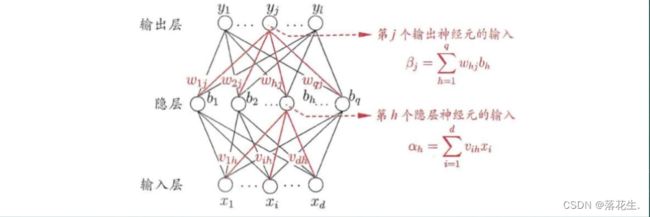
下图是一个三层的神经网络,输入层有d个节点,隐层有q个节点,输出层有l个节点。除了输入层,每一层的节点都包含一个非线性变换。

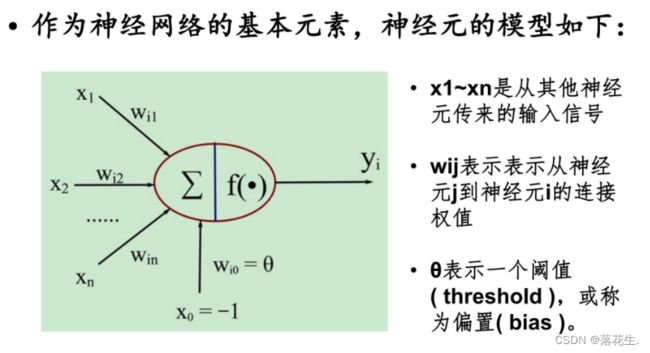
人工神经元
假设来自其他处理单元(神经元)i的信息为xi,与本处理单元的权重为ωi,i=0,1,…,n-1,处理单元内部的阈值为θ。


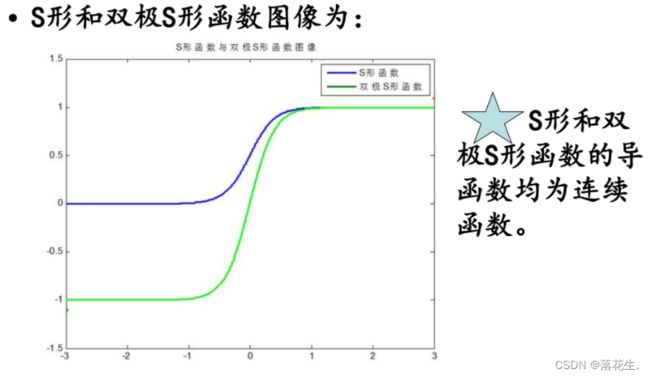
激活函数
网络模型
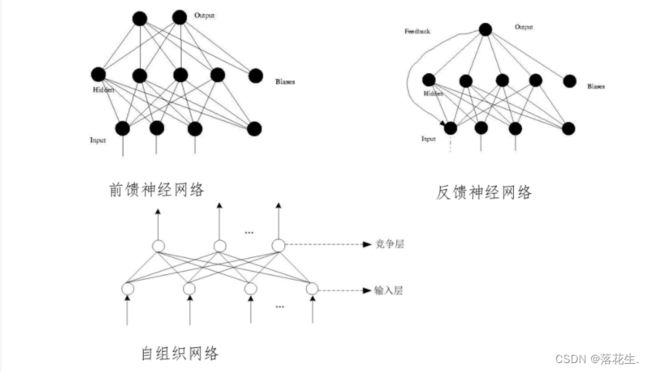
根据网络中神经元的互联方式的不同,网络模型分为:
前馈神经网络
只在训练过程会有反馈信号,而在分类过程中数据只能向前传送,直到到达输出层,层间没有向后的反馈信号
反馈神经网络
从输出到输入具有反馈连接的神经网络,其结构比前馈网络要复杂得多
自组织网络
通过自动寻找样本中的内在规律和本质属性,自组织、自适应地改变网络参数与结构。
神经网络的工作状态分为学习和工作两种状态
学习
利用学习算法来调整神经元间的连接权重,使得网络输出更符合实际
工作
神经元间的连接权值不变,可以作为分类器或者预测数据之用。
学习方式
学习分为有导师学习与无导师学习
有导师学习
将一组训练集送入网络,根据网络的实际输出与期望输出间的差别来调整连接权。
例如: BP算法
无导师学习
抽取样本集合中蕴含的统计特性,并以神经元之间的联接权的形式存于网络中。
例如: Hebb学习率
BP神经网络(Back Propagation)
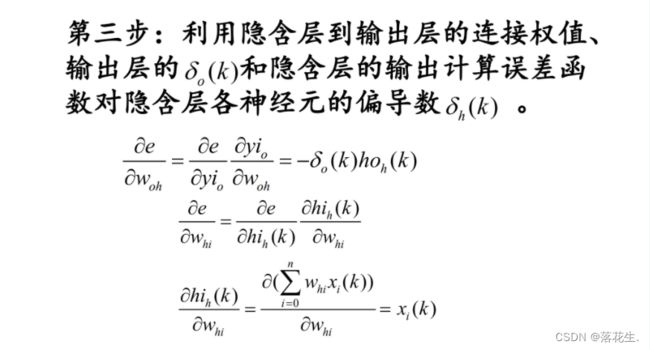
BP神经网络的学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输入层传入,经隐层逐层处理后,传向输出层若输出层的实际输出与期望输出不符,则转向误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。
BP(Back Propagation)神经网络模型是目前应用最为广泛的人工神经网络模型之一。BP 网络能学习和存贮大量的输入一输出模式映射关系,而无须事前揭示描述这种映射关系的数学方程。它的学习规则是使用梯度下降法,通过反向传播来不断调整网络的权值和阙值,使网络的误差平方和最小。BP 神经网络模型拓扑结构包括输入层(input)、隐含层(hidden layer)和输出层(output layer)。
输入层有多个输入结点;输出层有一个或多个输出结点;中间的隐含层结点个数根据实际需要进行设置,上、下两层之间的结点实现全连接,即下层的每一个结点都与上层的每一个结点实现全连接,而同一层结点之间无连接。
BP算法
数据预处理
1、数据预处理
在训练神经网络前一般需要对数据进行预处理,一种重要的预处理手段是归一化处理。下面简要介绍归一化处理的原理与方法
(1) 什么是归一化?
数据归一化,就是将数据映射到[0,1]或[-1,1]区间或更小的区间,比如(0.1,0.9)。
(2) 为什么要归一化处理?
<1>输入数据的单位不一样,有些数据的范围可能特别大,导致的结果是神经网络收敛慢、训练时间长。
<2>数据范围大的输入在模式分类中的作用可能会偏大,而数据范围小的输入作用就可能会偏小。
<3>由于神经网络输出层的激活函数的值域是有限制的,因此需要将网络训练的目标数据映射到激活函数的值域。
例如神经网络的输出层若采用S形激活函数,由于S形函数的值域限制在(0,1),也就是说神经网络的输出只能限制在(0,1),所以训练数据的输出就要归一化到[0,1]区间。
<4>S形激活函数在(0,1)区间以外区域很平缓,区分度太小。例如S形函数f(x)在参数a=1时,f(100)与f(5)只相差0.0067.


相关命令代码
数据预处理
神经网络的训练和测试
示例
设训练矩阵P为mn阶矩阵。m代表需要判断的参数(属性)的个数,n代表有多少组数据(样本)。
设产生的结果矩阵T为cn阶。c为输出结果的状态总共数,n要与P中的n相同,有多少组样本就要有多少组输出。
列:通过3门科目的评价60个孩子的成绩的好坏,结果只输出好或坏。此时P为3乘60维的矩阵,T为1乘60维的矩阵。
%以每三个月的销售量经归一化处理后作为输入,可以加快网络的训练速度将每组数据都变为-1至1之间的数
P=[0.5152 0.8173 1.0000;
0.8173 1.0000 0.7308;
1.0000 0.7308 0.1390;
0.7308 0.1390 0.1087;
0.1390 0.1087 0.3520;
0.1087 0.3520 0.0000;]';
%以第四个月的销售量归一化处理后作为目标向量
T=[0.7308 0.1390 0.1087 0.3520 0.0000 0.3761];
%创建一个BP神经网络,每一个输入向量的取值范围为[0,1],
% 输出层有一个神经元,隐含层的激活函数为tansig,
% 输出层的激活函数为logsig,训练函数为梯度下降函数
net=newff([0 1;0 1;0 1],[5,1],{'tansig','logsig'},'traingd');
net.trainParam.epochs=15000;%训练终止次数
net.trainParam.goal=0.01;%训练终止精度
net=train(net,P,T);%用P和T去训练
Y = sim(net,P)%用P去做仿真
plot(P,T,P,Y,'o')%画出图像
例子:采用动量梯度下降算法训练 BP 网络
% 训练样本定义如下:
% 输入矢量为
% p =[-1 -2 3 1
% -1 1 5 -3]
% 目标矢量为 t = [-1 -1 1 1]
close all
clear
clc
% ---------------------------------------------------------------
% NEWFF——生成一个新的前向神经网络,函数格式:
% net = newff(PR,[S1 S2...SNl],{TF1 TF2...TFNl},BTF,BLF,PF) takes,
% PR -- R x 2 matrix of min and max values for R input elements
% (对于R维输入,PR是一个R x 2 的矩阵,每一行是相应输入的边界值)
% Si -- 第i层的维数
% TFi -- 第i层的传递函数, default = 'tansig'
% BTF -- 反向传播网络的训练函数, default = 'traingdx'
% BLF -- 反向传播网络的权值/阈值学习函数, default = 'learngdm'
% PF -- 性能函数, default = 'mse'
% ---------------------------------------------------------------
% TRAIN——对 BP 神经网络进行训练,函数格式:
% train(NET,P,T,Pi,Ai,VV,TV),输入参数:
% net -- 所建立的网络
% P -- 网络的输入
% T -- 网络的目标值, default = zeros
% Pi -- 初始输入延迟, default = zeros
% Ai -- 初始网络层延迟, default = zeros
% VV -- 验证向量的结构, default = []
% TV -- 测试向量的结构, default = []
% 返回值:
% net -- 训练之后的网络
% TR -- 训练记录(训练次数及每次训练的误差)
% Y -- 网络输出
% E -- 网络误差
% Pf -- 最终输入延迟
% Af -- 最终网络层延迟
% ---------------------------------------------------------------
% SIM——对 BP 神经网络进行仿真,函数格式:
% [Y,Pf,Af,E,perf] = sim(net,P,PiAi,T)
% 参数与前同。
% ---------------------------------------------------------------
%
% 定义训练样本
% P 为输入矢量
echo on
P=[-1, -2, 3, 1;
-1, 1, 5, -3];
% T 为目标矢量
T=[-1, -1, 1, 1];
% 创建一个新的前向神经网络
net=newff(minmax(P),[3,1],{'tansig','purelin'},'traingdm')
% ---------------------------------------------------------------
% 训练函数:traingdm,功能:以动量BP算法修正神经网络的权值和阈值。
% 它的相关特性包括:
% epochs:训练的次数,默认:100
% goal:误差性能目标值,默认:0
% lr:学习率,默认:0.01
% max_fail:确认样本进行仿真时,最大的失败次数,默认:5
% mc:动量因子,默认:0.9
% min_grad:最小梯度值,默认:1e-10
% show:显示的间隔次数,默认:25
% time:训练的最长时间,默认:inf
% ---------------------------------------------------------------
% 当前输入层权值和阈值
inputWeights=net.IW{1,1}
inputbias=net.b{1}
% 当前网络层权值和阈值
layerWeights=net.LW{2,1}
layerbias=net.b{2}
% 设置网络的训练参数
net.trainParam.show = 50;
net.trainParam.lr = 0.05;
net.trainParam.mc = 0.9;
net.trainParam.epochs = 1000;
net.trainParam.goal = 1e-3;
% 调用 TRAINGDM 算法训练 BP 网络
[net,tr]=train(net,P,T);
% 对 BP 网络进行仿真
A = sim(net,P)
% 计算仿真误差
E = T - A
MSE=mse(E)
echo off
figure;
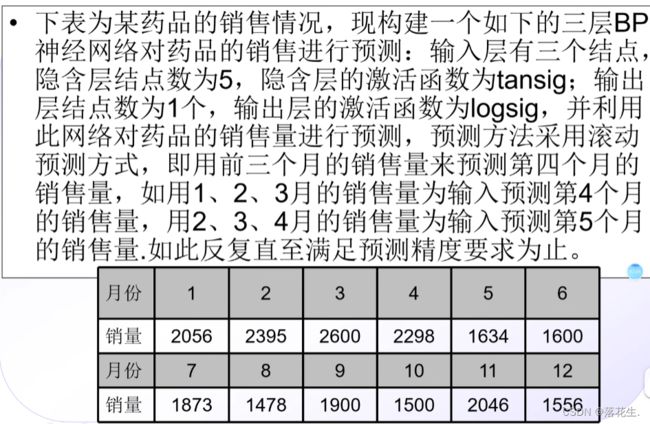
plot((1:4),T,'-*',(1:4),A,'-o')
运行结果
预测的准确度还是比较高的
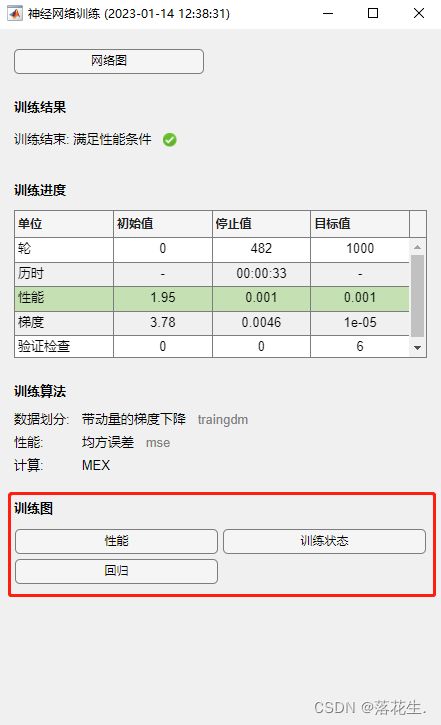
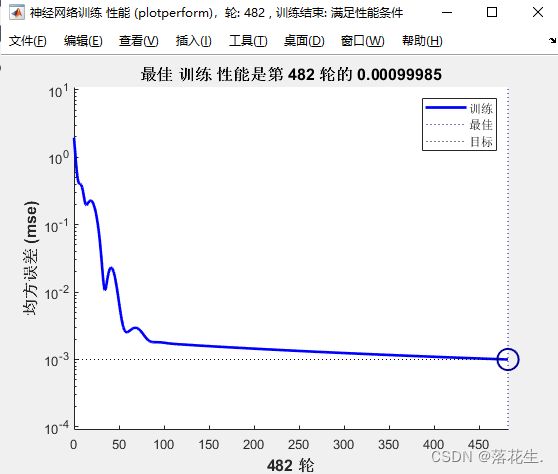
点击训练图可以得到训练过程中各个数据的变动结果
BP神经网络的优缺点
优点
- 非线性映射能力: BP神经网络实质上实现了一个从输入到输出的映射功能数学理论证明三层的神经网络就能够以任意精度逼近任何非线性连续函数。这使得其特别适合于求解内部机制复杂的问题,即BP神经网络具有较强的非线性映射能力。
2)自学习和自适应能力: BP神经网络在训练时,能够通过学习自动提取输出输出数据间的“合理规则”,并自适应的将学习内容记忆于网络的权值中。即BP神经网络具有高度自学习和自适应的能力。 - 泛化能力:所谓泛化能力是指在设计模式分类器时,即要考虑网络在保证对所需分类对象进行正确分类,还要关心网络在经过训练后,能否对未见过的模式或有噪声污染的模式,进行正确的分类。也即BP神经网络具有将学习成果应用于新知识的能力。
4)容错能力: BP神经网络在其局部的或者部分的神经元受到破坏后对全局的训练结果不会造成很大的影响,也就是说即使系统在受到局部损伤时还是可以正常工作的。即BP神经网络具有一定的容错能力。
缺点
1、局部极小化问题: 从数学角度看,传统的 BP神经网络为一种局部搜索的优化方法,它要解决的是一个复杂非线性化问题,网络的权值是通过沿局部改善的方向逐渐进行调整的,这样会使算法陷入局部极值,权值收敛到局部极小点,从而导致网络训练失败。加上BP神经网络对初始网络权重非常敏感,以不同的权重初始化网络,其往往会收敛于不同的局部极小,这也是很多学者每次训练得到不同结果的根本原因。
2、BP 神经网络算法的收敛速度慢: 由于BP神经网络算法本质上为梯度下降法,它所要优化的目标函数是非常复杂的,因此,必然会出现“锯齿形现象”,这使得BP算法低效;又由于优化的目标函数很复杂,它必然会在神经元输出接近0或1的情况下,出现一些平坦区,在这些区域内,权值误差改变很小,使训练过程几乎停顿;BP神经网络模型中,为了使网络执行BP算法,不能使用传统的一维搜索法求每次迭代的步长,而必须把步长的更新规则预先赋予网络,这种方法也会引起算法低效。以上种种,导致了BP神经网络算法收敛速度慢的现象。
3、BP 神经网络结构选择不一: BP神经网络结构的选择至今尚无一种统一而完整的理论指导,一般只能由经验选定。网络结构选择过大,训练中效率不高,可能出现过拟合现象,造成网络性能低,容错性下降,若选择过小,则又会造成网络可能不收敛。而网络的结构直接影响网络的逼近能力及推广性质。因此,应用中如何选择合适的网络结构是一个重要的问题。
4、应用实例与网络规模的矛盾问题: BP神经网络难以解决应用问题的实例规模和网络规模间的矛盾问题,其涉及到网络容量的可能性与可行性的关系问题,即学习复杂性问题。
5、BP神经网络预测能力和训练能力的矛盾问题: 预测能力也称泛化能力或者推广能力,而训练能力也称逼近能力或者学习能力。一般情况下,训练能力差时,预测能力也差,并且一定程度上,随着训练能力地提高,预测能力会得到提高。但这种趋势不是固定的,其有一个极限,当达到此极限时,随着训练能力的提高,预测能力反而会下降,也即出现所谓“过拟合”现象。出现该现象的原因是网络学习了过多的样本细节导致,学习出的模型已不能反映样本内含的规律,所以如何把握好学习的度,解决网络预测能力和训练能力间矛盾问题也是BP神经网络的重要研究内容
6、BP神经网络样本依赖性问题: 网络模型的逼近和推广能力与学习样本的典型性密切相关,而从问题中选取典型样本实例组成训练集是一个很困难的问题。
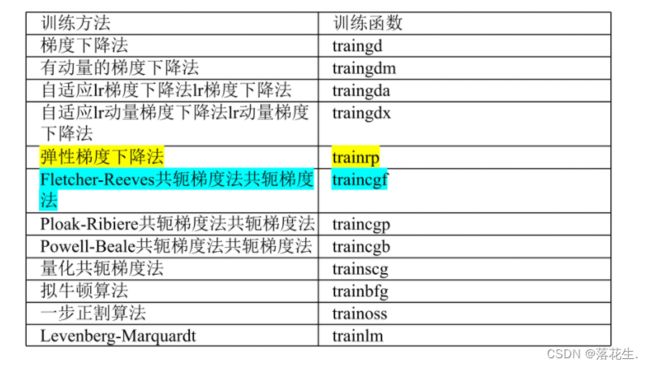
传统的BP算法改进主要有两类:
启发式算法: 如附加动量法,自适应算法
数值优化法: 如共扼梯度法、牛顿迭代法、Levenberg-Marquardt算法