Andrew Ng 神经网络与深度学习 week3
文章目录
-
- 神经网络的表示:
-
- 双层神经网络的表示
- 计算神经网络的输出
- 多个训练样本的向量化实现
-
- 将其向量化
- 向量化实现的解释
- 总结:
- 推理演绎
- Activation function
-
- tanh函数(对sigmoid函数做一定平移得到的新的函数)
- **Relu函数(修正线性单元)**
-
- 总结:
- Why we need to use the activation function?
- **激活函数的导数**
-
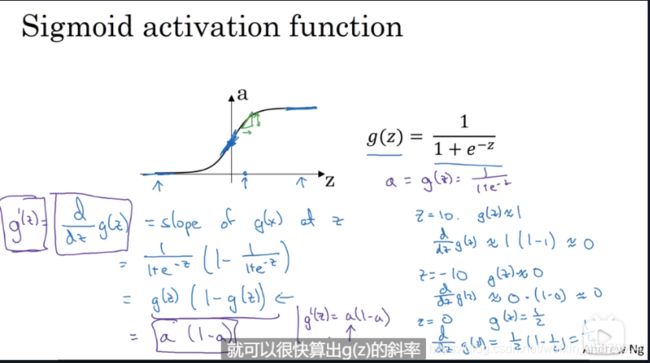
- sigmoid
- Tanh
- ReLu and Leaky ReLu
- **神经网络的梯度下降法**
-
-
- 反向传播六个式子的计算过程
- 总结:
-
- 随机初始化(random initialization)
- 样本数据预处理中的中心化和标准化处理
- np.sum
- 使用神经网络进行深度学习的步骤
- 编程作业第三周答案
- np.mean求取均值
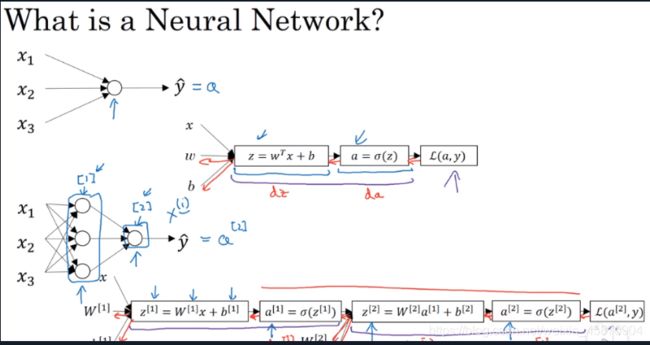
神经网络的表示:
[i]表示在神经网络的哪一层
双层神经网络的表示
值得注意的是一般把输入层都当作第0层 所以这个神经网络被称之为双层神经网络
计算神经网络的输出
向量化的经验法则就是进行堆叠(stacking),一般都是进行纵向堆叠
X = a [ 0 ] X=a^{[0]} X=a[0]
X = a [ 0 ] X=a^{[0]} X=a[0] 代码中对于只有一个隐藏层的神经网络只需要计算右边四个向量化的式子即可
通过把不同训练样本堆叠起来构成矩阵实现向量化就能够利用GPU(图像处理工具) or CPU的并行化计算功能从而一次性计算我的整个训练集
调GPU给tensorflow使用
recap up 归纳一下
多个训练样本的向量化实现
将其向量化
对于A 矩阵堆叠后 横向对应的不同的训练样本 纵向对应的是隐藏层中的第几个隐藏单元
对于X 横向对应的是不同的训练样本 纵向对应的不同的特征 也就是输入层的第几个结点
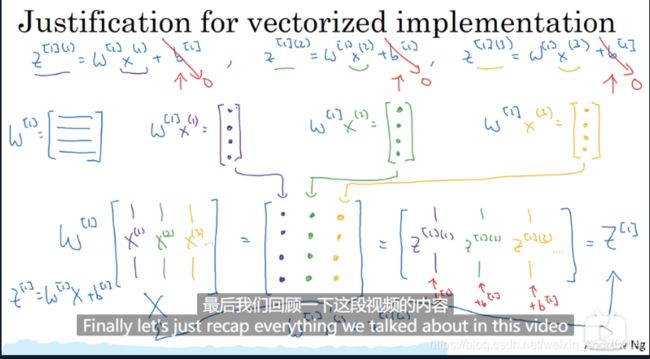
向量化实现的解释
总结:
右上方是原来带有for循环的代码 右下方是经过向量化实现后的代码
推理演绎
若有三个特征三个样本 W的维度和样本数无关 因为有4个神经元 三个特征 所以W的维度是(3,4)
X的维度是(nx,m)=(3,3)
b的维度只与样本有关=(1,3)
z [ 1 ] z^{[1]} z[1]的维度和 W [ 1 ] W^{[1]} W[1]就是(4,3)
w [ 2 ] w^{[2]} w[2]的维度 因为4个神经元 所以是(4,1)
b [ 2 ] b^{[2]} b[2]的维度 应该样本数量保持一致 所以还是(1,3)
最后W转置与 A [ 1 ] A^{[1]} A[1]相乘 就变成了(1,3)
得到最后的结果 三个样本的三个 y ^ \hat{y} y^ 一个三元素一维行向量
分清楚行向量和列向量的关键在于分清秩(rank)
Activation function
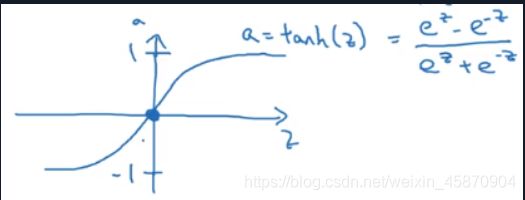
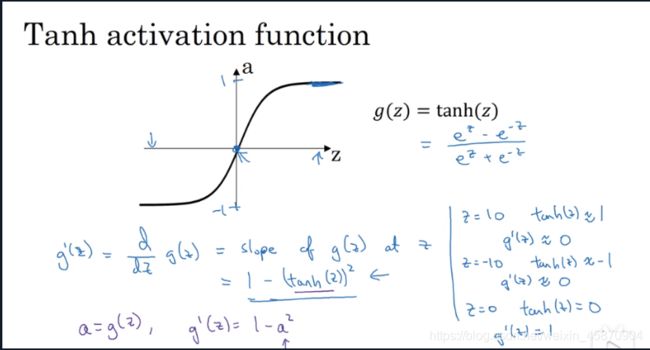
tanh函数(对sigmoid函数做一定平移得到的新的函数)
值位于(-1,1) tanh函数有直接对数据进行中心化预处理的作用
但是在一些场合 需要输出函数值位于(0,1)的时候 还是可以将输出函数用sigmoid函数 例如前面介绍的逻辑回归二分类问题
用上标方括号来区分在不同层的不同的激活函数
它和sigmoid函数都有一个缺点 当z值很大的时候 函数值位于的位置的斜率也就是梯度会相对较小,这不利于我们进行梯度下降算法
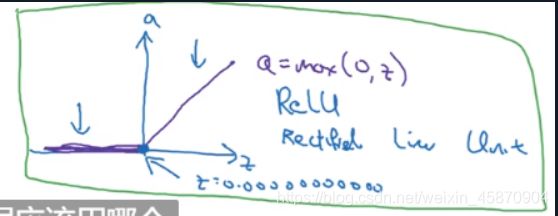
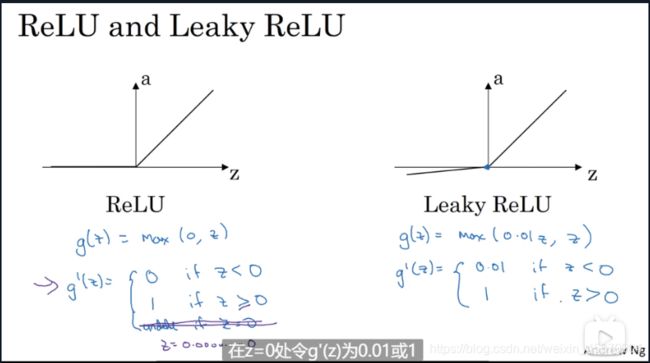
Relu函数(修正线性单元)
不确定用啥就用ReLu函数 可以令Z>0
**没有导数接近0的效应 **
总结:
0.01可以当做一个神经网络的参数 可以进行改变
Why we need to use the activation function?
如果没有激活函数 我们的神经网络一直进行计算的只是输入特征的线性组合 无论有多少隐藏层都是无意义的
所以 线性隐藏层是没有意义的 线性函数的组合依旧是线性函数 永远不能计算出有趣的非线性函数
当然一些简单的栗子
比如一元线性回归 就只是需要线性函数可能是可行的 比如预测房价(但房价是非负的 Relu作为输出层激活函数或许会更好)*
输入等于输出 g(z)=z 的这种函数叫做恒定激活函数
激活函数的导数
sigmoid
Tanh
ReLu and Leaky ReLu
神经网络的梯度下降法
值得注意的是 keepdims的开关不要忘记 其能使得np.sum计算出的结果包含矩阵特性
而不是直接计算出一个rank为1的向量(n,)
d z [ 1 ] dz^{[1]} dz[1]那里不是矩阵相乘 而是元素相乘 在编写代码的时候要尤其注意
右边的反向传播的六个式子 是我们编写代码的关键 一定切记
反向传播六个式子的计算过程
总结:
这部分的数学推导除了需要线性代数还需要矩阵论 矩阵求导的一些知识 暂时可以先记住
需要注意这里算出来这六个式子的依据是逻辑回归独特的误差函数 并不是大家常用的平方误差函数
n [ 0 ] n^{[0]} n[0] 代表输入的特征数 n [ 1 ] n^{[1]} n[1] 代表第一个隐藏层的神经元个数 n [ 2 ] n^{[2]} n[2] 代表输出层(第三层)的个数
推断代码是否可能出现问题的关键就在于将矩阵的维度进行匹配,还有就是dw和w的维度是一样的
例如 w [ 1 ] w^{[1]} w[1]的维度就是( n [ 1 ] , n [ 0 ] n^{[1]},n^{[0]} n[1],n[0]) b [ 1 ] b^{[1]} b[1]的维度一般是( n [ 1 ] , 1 n^{[1]},1 n[1],1)这也是符合常理的 每一个神经元都应该有和特征数相同的w数量 注意模型的特性不要和样本数混到一起 这就是为什么 w b等模型本身的参数都要除以m进行归一化的原因
注意这里 w [ 1 ] w^{[1]} w[1]的维度是不需要再转置的 已经经过处理了
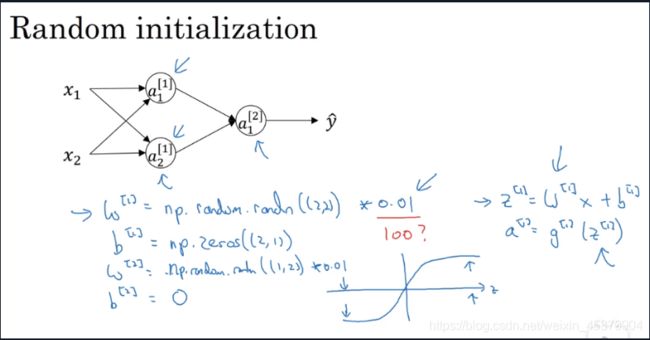
随机初始化(random initialization)
之所以不采用初始化为0的方法是因为如果初始化为0 各个神经元的计算效果都完全一样 所占的权重也完全相同 多个神经元就失去了意义 所以我们采用随机初始化 且一般将初始化参数设为一个较小的值 以防止激活函数过早达到饱和从而导致梯度下降效率变低 让w-dw后对于a z等都会有更加明显的变化.
样本数据预处理中的中心化和标准化处理
在回归问题和一些机器学习算法中,以及训练神经网络的过程中,通常需要对原始数据进行中心化(Zero-centered或者Mean-subtraction)处理和标准化(Standardization或Normalization)处理。
目的:通过中心化和标准化处理,得到均值为0,标准差为1的服从标准正态分布的数据。
概率论所学
χ ′ = χ − u σ \chi'=\frac{\chi-u}{\sigma} χ′=σχ−u
简言之,当原始数据不同维度上的特征的尺度(单位)不一致时,需要标准化步骤对数据进行预处理。
下图中以二维数据为例:左图表示的是原始数据;中间的是中心化后的数据,数据被移动大原点周围;右图将中心化后的数据除以标准差,得到为标准化的数据,可以看出每个维度上的尺度是一致的(红色线段的长度表示尺度)。
其实,在不同的问题中,中心化和标准化有着不同的意义,
比如在训练神经网络的过程中,通过将数据标准化,能够加速权重参数的收敛。
另外,对于主成分分析(PCA)问题,也需要对数据进行中心化和标准化等预处理步骤。
np.sum
当axis为0时,是压缩行,即将每一列的元素相加,将矩阵压缩为一行
当axis为1时,是压缩列,即将每一行的元素相加,将矩阵压缩为一列
使用神经网络进行深度学习的步骤
The general methodology to build a Neural Network is to:
1. Define the neural network structure ( # of input units, # of hidden units, etc).
2. Initialize the model's parameters
3. Loop:
- Implement forward propagation
- Compute loss
- Implement backward propagation to get the gradients
- Update parameters (gradient descent)
You often build helper functions to compute steps 1-3 and then merge them into one function we call nn_model(). Once you’ve built nn_model() and learnt the right parameters, you can make predictions on new data.
编程作业第三周答案
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
#%matplotlib inline #如果你使用用的是Jupyter Notebook的话请取消注释。
np.random.seed(1) #设置一个固定的随机种子,以保证接下来的步骤中我们的结果是一致的。
X, Y = load_planar_dataset()
#plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral) #绘制散点图
shape_X = X.shape
shape_Y = Y.shape
m = Y.shape[1] # 训练集里面的数量
print ("X的维度为: " + str(shape_X))
print ("Y的维度为: " + str(shape_Y))
print ("数据集里面的数据有:" + str(m) + " 个")
def layer_sizes(X , Y):
"""
参数:
X - 输入数据集,维度为(输入的数量,训练/测试的数量)
Y - 标签,维度为(输出的数量,训练/测试数量)
返回:
n_x - 输入层的数量
n_h - 隐藏层的数量
n_y - 输出层的数量
"""
n_x = X.shape[0] #输入层
n_h = 4 #,隐藏层,硬编码为4
n_y = Y.shape[0] #输出层
return (n_x,n_h,n_y)
def initialize_parameters( n_x , n_h ,n_y):
"""
参数:
n_x - 输入节点的数量
n_h - 隐藏层节点的数量
n_y - 输出层节点的数量
返回:
parameters - 包含参数的字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
"""
np.random.seed(2) #指定一个随机种子,以便你的输出与我们的一样。
W1 = np.random.randn(n_h,n_x) * 0.01
b1 = np.zeros(shape=(n_h, 1))
W2 = np.random.randn(n_y,n_h) * 0.01
b2 = np.zeros(shape=(n_y, 1))
#使用断言确保我的数据格式是正确的
assert(W1.shape == ( n_h , n_x ))
assert(b1.shape == ( n_h , 1 ))
assert(W2.shape == ( n_y , n_h ))
assert(b2.shape == ( n_y , 1 ))
parameters = {"W1" : W1,
"b1" : b1,
"W2" : W2,
"b2" : b2 }
return parameters
def forward_propagation( X , parameters ):
"""
参数:
X - 维度为(n_x,m)的输入数据。
parameters - 初始化函数(initialize_parameters)的输出
返回:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型变量
"""
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
#前向传播计算A2
Z1 = np.dot(W1 , X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2 , A1) + b2
A2 = sigmoid(Z2)
#使用断言确保我的数据格式是正确的
assert(A2.shape == (1,X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return (A2, cache)
def compute_cost(A2,Y,parameters):
"""
计算方程(6)中给出的交叉熵成本,
参数:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
Y - "True"标签向量,维度为(1,数量)
parameters - 一个包含W1,B1,W2和B2的字典类型的变量
返回:
成本 - 交叉熵成本给出方程(13)
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
#计算成本
logprobs = logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))
cost = - np.sum(logprobs) / m
cost = float(np.squeeze(cost))
assert(isinstance(cost,float))
return cost
def backward_propagation(parameters,cache,X,Y):
"""
使用上述说明搭建反向传播函数。
参数:
parameters - 包含我们的参数的一个字典类型的变量。
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型的变量。
X - 输入数据,维度为(2,数量)
Y - “True”标签,维度为(1,数量)
返回:
grads - 包含W和b的导数一个字典类型的变量。
"""
m = X.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
A1 = cache["A1"]
A2 = cache["A2"]
dZ2= A2 - Y
dW2 = (1 / m) * np.dot(dZ2, A1.T)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
dW1 = (1 / m) * np.dot(dZ1, X.T)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2 }
return grads
def update_parameters(parameters,grads,learning_rate=1.2):
"""
使用上面给出的梯度下降更新规则更新参数
参数:
parameters - 包含参数的字典类型的变量。
grads - 包含导数值的字典类型的变量。
learning_rate - 学习速率
返回:
parameters - 包含更新参数的字典类型的变量。
"""
W1,W2 = parameters["W1"],parameters["W2"]
b1,b2 = parameters["b1"],parameters["b2"]
dW1,dW2 = grads["dW1"],grads["dW2"]
db1,db2 = grads["db1"],grads["db2"]
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def nn_model(X,Y,n_h,num_iterations,print_cost=False):
"""
参数:
X - 数据集,维度为(2,示例数)
Y - 标签,维度为(1,示例数)
n_h - 隐藏层的数量
num_iterations - 梯度下降循环中的迭代次数
print_cost - 如果为True,则每1000次迭代打印一次成本数值
返回:
parameters - 模型学习的参数,它们可以用来进行预测。
"""
np.random.seed(3) #指定随机种子
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
parameters = initialize_parameters(n_x,n_h,n_y)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
for i in range(num_iterations):
A2 , cache = forward_propagation(X,parameters)
cost = compute_cost(A2,Y,parameters)
grads = backward_propagation(parameters,cache,X,Y)
parameters = update_parameters(parameters,grads,learning_rate = 0.5)
if print_cost:
if i%1000 == 0:
print("第 ",i," 次循环,成本为:"+str(cost))
return parameters
def predict(parameters,X):
"""
使用学习的参数,为X中的每个示例预测一个类
参数:
parameters - 包含参数的字典类型的变量。
X - 输入数据(n_x,m)
返回
predictions - 我们模型预测的向量(红色:0 /蓝色:1)
"""
A2 , cache = forward_propagation(X,parameters)
predictions = np.round(A2)
return predictions
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000, print_cost=True)
#绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
"""
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50] #隐藏层数量
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i + 1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations=5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
print ("隐藏层的节点数量: {} ,准确率: {} %".format(n_h, accuracy))
"""
得到的结论是:
-
使用神经网络确实可以训练出强大的非线性函数 而简单地使用logistic regression一般只能处理线性二分类问题
-
增加隐藏层的个数有利于模型的更高准确率
-
一般来说 输出层只有一个神经元 根据实际情况而定
-
用神经网络去拟合一个非线性函数(决策边界(decision boundary) 来实现较为二分类问题(binary classfication)