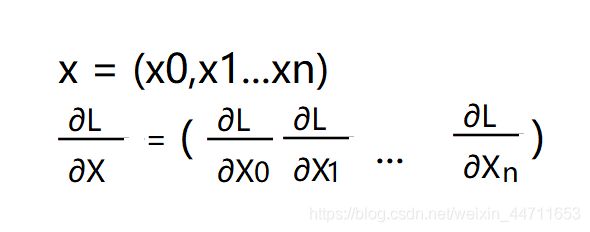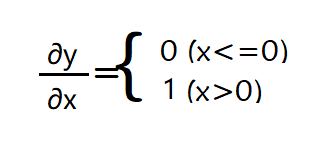深度学习笔记---在计算图思想下实现简单神经网络的各个计算层
# 1.导入
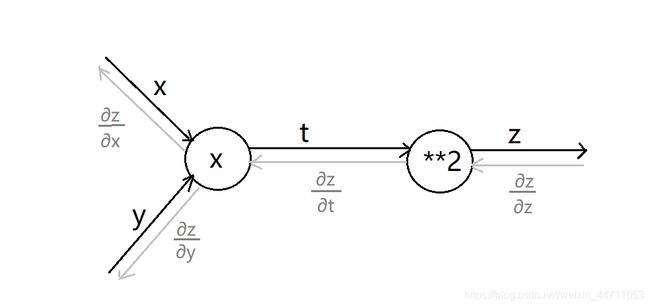
在上篇博客中,例子z = (x+y)^2的计算层就是两个节点。
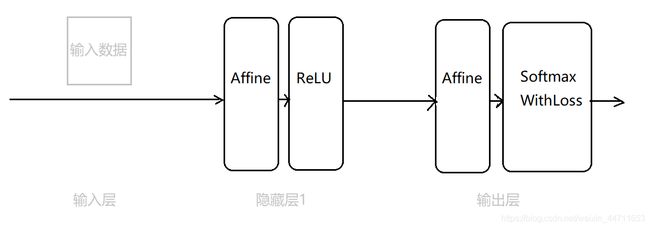
二层神经网络利用计算图的思想可以按照如下简单表示
上图中的黑色框均表示计算层,Affine表示加权和层,ReLU表示ReLU激活函数层,SoftmaxWithLoss表示Softmax激活函数和Loss损失函数的组合层。
# 2.用Python实现各个计算层
1.Affine层的实现
求加权和的过程就是X*W+B。(X表示数据矩阵,W表示权重矩阵,B表示偏置矩阵)
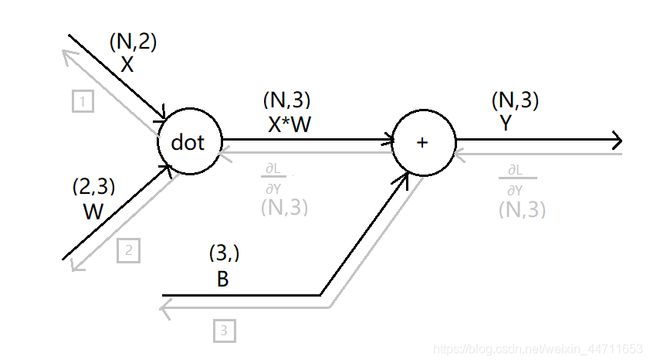
首先我们可以得到如下Affine层的具体计算图
上图中每个确定的数据以及它的形状都已标识出来。(数据矩阵X形状假设为N*2,权重矩阵W假设为2*3,其中的L表示神经网络的最后输出)
灰色方框表示暂时还不确定的三个数据。下面我们来进行推理。
首先,根据如下数学式,易知X和∂L/∂X形状一致,W和∂L/∂W形状一致,B和∂L/∂B形状一致。
所以方框1的形状是N*2,方框2的形状是2*3,方框3的形状是1*3。
其次,如果上述X*W仅是普通两个数字的乘法,那么方框1就等于上游传来的导数∂L/∂Y乘以W(也就是乘以∂X*W/∂X)。虽然X*W表示的是两个矩阵的乘法,不能直接如上计算。但是矩阵的乘法中包含了普通数字的乘法,所以可知∂X*W/∂X必定与W有关。然后,我们再依据方框1的形状和矩阵乘法中对应维度必须一致的要求,可以推得方框1就是∂L/∂Y乘以W的转置。同理可得,方框2就是X的转置乘以∂L/∂Y。
最后,我们来考虑方框3。一般来说,矩阵的加法要求两个矩阵形状一致,当两个矩阵形状一致时,反向传播只需将上游传来的导数原封不动地传给下游。但是利用python的广播功能,正向传播时X*W+B是可以被正确计算的(也就是X*W(N*3)当中的每一行都加了一次B(1*3))。对于此时的反向传播,∂L/∂Y(N*3)也需要汇总为∂L/∂B(1*3),也就是∂L/∂B(方框3)等于∂L/∂Y垂直方向上的和。
综上所述,Affine层的实现如下所示:
# Affine层(计算加权和)
class Affine:
def __init__(self,W,b): # 加权和层初始化时要求入口参数为该层的权重W和偏置b
self.W = W
self.b = b
self.x = None # 用于计算反向传播时W的梯度
self.dW = None # 用于存储反向传播时计算出的W的梯度
self.db = None # 用于存储反向传播时计算出的b的梯度
def forward(self,x): # 前向函数就是通过x,W和b计算出加权和,再输出
self.x = x
out = np.dot(x,self.W) + self.b
return out
def backward(self,dout): # 反向函数就是将上游传来的导数dout乘以权重矩阵的转置WT后输出(反向函数的输出永远是上游传来的导数乘以该层正向输出对正向输入的偏导)
dx = np.dot(dout,self.W.T)
self.dW = np.dot(self.x.T,dout) # 顺便计算出上游导数关于该层权重和偏置的导数,实际上就是求出了损失函数关于该层权重和偏置的梯度
self.db = np.sum(dout,axis=0)
return dx2.ReLU层的实现
激活函数ReLU的数学式如下图所示
我们可以依此求出y关于x的导数如下图所示
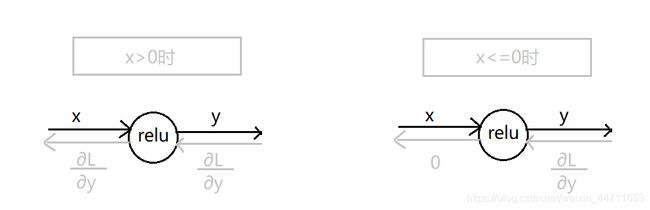
所以ReLU层的计算图就可以如下图表示
综上所述,ReLU层的实现如下所示
# ReLU层
class ReLU:
def __init__(self):
self.mask = None # 初始化实例变量mask(mask用来区分输入数组中x<=0的情况)
# 前向函数,将输入数组x中小于等于0的部分置为0后输出
def forward(self,x): # 前向函数forward的入口参数为调用该函数的对象self,和一个输入numpy数组(代表加权和数组)
self.mask = (x<=0) # 用(x<=0)为实例变量mask赋值,(x<=0)表示一个boolean型的数组(x中值<=0的位置为True,值>0的位置为False)
out = x.copy() # 定义输出信号out为一个与x相同的numpy数组
out[self.mask] = 0 # 将out数组中mask为True的地方设为0
return out
# 反向函数,将输入数组dout中正向传播时小于等于0的部分置0后输出
def backward(self,dout): # 后向函数backward的入口参数为调用该函数的对象self,和一个上游传来的导数dout
dout[self.mask] = 0 # 将dout数组中mask为True的地方设为0
dx = dout
return dx3.SoftmaxWithLoss层的实现
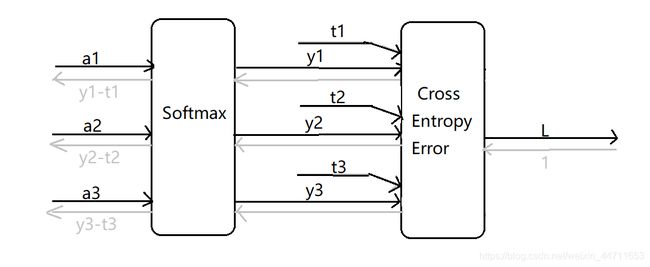
SoftmaxWithLoss层的具体推导过程比较复杂,下面给出该层结论性的简易版计算图
SoftmaxWithLoss层首先经过Softmax激活函数计算层将加权和形式解a转换为概率形式解y,再经过CrossEntropyError损失函数计算层根据推理结果y和正确解标签t计算得到损失函数值L,并输出。反向传播时,整个SoftmaxWithLoss层输入为1(也就是∂L/∂L),输出为推理结果与正确解的差分y-t。(这里十分巧妙地实现了将推理结果与正确解标签之间的误差信息传给前面的层,这是因为交叉熵误差函数CrossEntropyError就是为了得到这个结果而设计的)
综上所述,SoftmaxWithLoss层的实现如下所示
# SoftmaxWithLoss层(正规化和计算损失函数)
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 存储损失函数值
self.y = None # 存储softmax的输出
self.t = None # 存储正确解标签(one-hot表示)
def forward(self,x,t): # 前向函数,输出损失函数值
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y,self.t)
return self.loss
def backward(self,dout=1): # 反向函数,输出推理结果与正确解标签的差分
batch_size = self.t.shape[0] # 用batch_size记录当前批数据的大小(一次处理的图像数目)
dx = (self.y-self.t)/batch_size # 除以batch_size后得到的是单个图像的误差
return dx
# 本博客参考了《深度学习入门——基于Python的理论与实现》(斋藤康毅著,陆宇杰译),特在此声明。