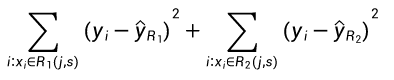适合小白入门的随机森林介绍
作者:Abner,王宇
一、随机森林简介
随机森林是机器学习中的一种常用方法,而随机森林背后的思想,更是与群体智慧,甚至“看不见的手”相互映照。
上世纪八十年代Breiman等人发明分类树的算法(Breimanet al. 1984),通过反复二分数据进行分类或回归,计算量大大降低。2001年Breiman把分类树组合成随机森林(Breiman2001a),即在变量(列)的使用和数据(行)的使用上进行随机化,生成很多分类树,再汇总分类树的结果。随机森林在运算量没有显著提高的前提下提高了预测精度。随机森林对多元公线性不敏感,结果对缺失数据和非平衡的数据比较稳健,可以很好地预测多达几千个解释变量的作用(Breiman2001b),被誉为当前最好的算法之一(Iversonet al. 2008)。
随机森林顾名思义,是用随机的方式建立一个森林,森林里面有很多的决策树组成,随机森林的每一棵决策树之间是没有关联的。在得到森林之后,当有一个新的输入样本进入的时候,就让森林中的每一棵决策树分别进行一下判断,看看这个样本应该属于哪一类(对于分类算法),然后看看哪一类被选择最多,就预测这个样本为那一类。随机森林可以既可以处理属性为离散值的量,也可以处理属性为连续值的量。另外,随机森林还可以用来进行无监督学习聚类和异常点检测。所以在学习随机森林之前,要了解一些决策树的知识。
二、决策树
1.决策树简介
决策树是一种监督学习算法。它适用于类别和连续输入(特征)和输出(预测)变量。基于树的方法把特征空间划分成一系列矩形,然后给每一个矩形安置一个简单的模型(像一个常数)。从概念上来讲,它们是简单且有效的。首先我们通过一个例子来理解决策树。
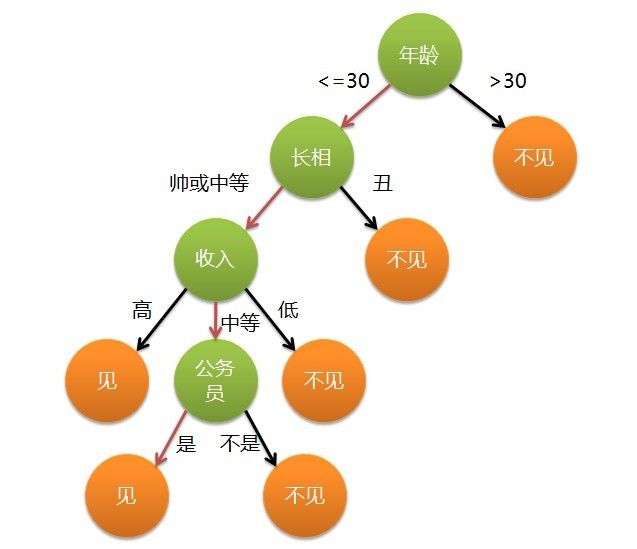
决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
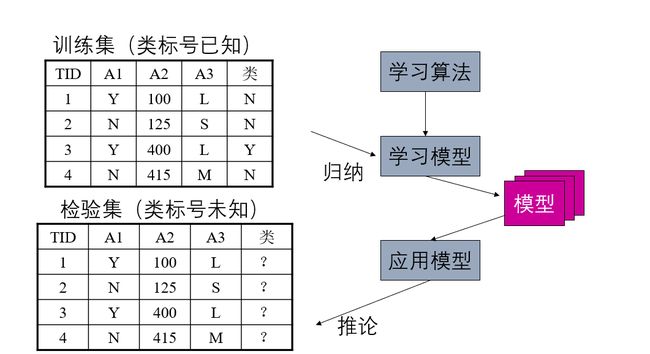
通过上面的例子,我们可以总结分类问题一般包括两个步骤:
1、模型构建(归纳)
通过对训练集合的归纳,建立分类模型。
2、预测应用(推论)
根据建立的分类模型,对测试集合进行测试。
决策树是一种典型的分类方法
1.首先对数据进行处理,利用归纳算法生成可读的规则和决策树,
2.然后使用决策对新数据进行分析。
注意:本质上决策树是通过一系列规则对数据进行分类的过程。
决策树的优点
1、推理过程容易理解,决策推理过程可以表示成IfThen形式;
2、推理过程完全依赖于属性变量的取值特点;
3、可自动忽略目标变量没有贡献的属性变量,也为判断属性变量的重要性,减少变量的数目提供参考。
决策树的分类包括回归树和分类树
1、回归树
我们现在关注一下回归树的算法的细节。简要来说,创建一个决策树包含两步:
1. 把预测器空间,即一系列可能值![]() ,分成J个不同的且非重叠的区域
,分成J个不同的且非重叠的区域![]() 。
。
2. 对进入区域 ![]() 的每一个样本观测值都进行相同的预测,该预测就是
的每一个样本观测值都进行相同的预测,该预测就是 ![]() 中训练样本预测值的均值。
中训练样本预测值的均值。
为了创建 J 个区域 ![]() ,预测器区域被分为高维度的矩形或盒形。其目的在于通过下列式子找到能够使 RSS 最小化的盒形区域
,预测器区域被分为高维度的矩形或盒形。其目的在于通过下列式子找到能够使 RSS 最小化的盒形区域 ![]() ,
,
其中,![]() 即是第 j 个盒形中训练观测的平均预测值。
即是第 j 个盒形中训练观测的平均预测值。
鉴于这种空间分割在计算上是不可行的,因此我们常使用贪婪方法(greedy approach)来划分区域,叫做递归二元分割(recursive binary splitting)。
它是贪婪的(greedy),这是因为在创建树过程中的每一步骤,最佳分割都会在每个特定步骤选定,而不是对未来进行预测,并选取一个将会在未来步骤中出现且有助于创建更好的树的分隔。注意所有的划分区域 ![]() 都是矩形。为了进行递归二元分割,首先选取预测器
都是矩形。为了进行递归二元分割,首先选取预测器 ![]() 和切割点 s
和切割点 s
其中 ![]() 为区域
为区域 ![]() 中观察样本的平均预测值,
中观察样本的平均预测值,![]() 为区域
为区域 ![]() 的观察样本预测均值。这一过程不断重复以搜寻最好的预测器和切分点,并进一步分隔数据以使每一个子区域内的 RSS 最小化。然而,我们不会分割整个预测器空间,我们只会分割一个或两个前面已经认定的区域。这一过程会一直持续,直到达到停止准则,例如我们可以设定停止准则为每一个区域最多包含 m 个观察样本。一旦我们创建了区域
的观察样本预测均值。这一过程不断重复以搜寻最好的预测器和切分点,并进一步分隔数据以使每一个子区域内的 RSS 最小化。然而,我们不会分割整个预测器空间,我们只会分割一个或两个前面已经认定的区域。这一过程会一直持续,直到达到停止准则,例如我们可以设定停止准则为每一个区域最多包含 m 个观察样本。一旦我们创建了区域 ![]() ,给定一个测试样本,我们就可以用该区域所有训练样本的平均预测值来预测该测试样本的值。
,给定一个测试样本,我们就可以用该区域所有训练样本的平均预测值来预测该测试样本的值。
2.分类树
分类树和回归树十分相似,只不过它是定性地预测响应值而非定量预测。从上文可知,回归树对一个观察值所预测的连续型数值就是属于同一叶结点训练样本观察值的均值。但是对于分类树来说,我们所预测的类别是训练样本观察值在某区域下最常见的类别,即训练观察值的模式响应(mode response)。为了达到分类目的,很多时候系统并不会只预测一个类别,它常常预测一组类别及其出现的概率。
分类树的生成和回归树的生成十分相似。正如在回归树中那样,我们一般使用递归性的二元分割来生成分类树。然而在分类树中,RSS 不能作为二元分割的标准。我们需要定义叶结点的不纯度量 Q_m 来替代 RSS,即一种可以在子集区域 R_1,R_2,...,R_j 度量目标变量同质性的方法。在结点 m 中,我们可以通过 N_m 个样本观察值表示一个区域 R_m 所出现类别的频率,第 k 个类别在第 m 个区域下训练所出现的频率可表示为:
其中,I(![]() =k) 为指示函数,即如果
=k) 为指示函数,即如果 ![]() = k,则取 1,否则取零。
= k,则取 1,否则取零。
不纯性度量 ![]() 一个比较自然的方法是分类误差率。分类误差率描述的是训练观察值在某个区域内不属于最常见类别的概率:
一个比较自然的方法是分类误差率。分类误差率描述的是训练观察值在某个区域内不属于最常见类别的概率:
![]()
考虑到该函数不可微,因此它不能实现数值优化。此外,该函数在结点概率改变上并不敏感,因此这种分类误差率对于生成树十分低效。我们一般使用 Gini 指数和交叉熵函数来衡量结点的误差度量。
Gini 指数可以衡量 k 个类别的总方差,它一般定义为:
较小的 Gini 指数值表示结点包含了某个类别大多数样本观察值。
在信息论里面,交叉熵函数用来衡量系统的混乱度。对于二元系统来说,如果系统包含了一个类别的所有内容,那么它的值为零,而如果两个类别的数量一样多,那么交叉熵达到最大为 1。因此,和 Gini 指数一样,交叉熵函数同样能用于度量结点的不纯度:
和 G 一样,较小的 S 值表示区域内结点包含了单个类别中的大多数观察值。
决策树常见参数和概念
如果我们希望以数学的方式理解决策树,我们首先需要了解决策树和树型学习算法的一般概念。理解以下的术语同样能帮助我们调整模型。
根结点:表示所有数据样本并可以进一步划分为两个或多个子结点的父结点。
分裂(Splitting):将一个结点划分为两个或多个子结点的过程。
决策结点:当一个子结点可进一步分裂为多个子结点,那么该结点就称之为决策结点。
叶/终止结点:不会往下进一步分裂的结点,在分类树中代表类别。
分枝/子树:整棵决策树的一部分。
父结点和子结点:如果一个结点往下分裂,该结点称之为父结点而父结点所分裂出来的结点称之为子结点。
结点分裂的最小样本数:在结点分裂中所要求的最小样本数量(或观察值数量)。这种方法通常可以用来防止过拟合,较大的最小样本数可以防止模型对特定的样本学习过于具体的关系,该超参数应该需要使用验证集来调整。
叶结点最小样本数:叶结点所要求的最小样本数。和结点分裂的最小样本数一样,该超参数同样也可以用来控制过拟合。对于不平衡类别问题来说,我们应该取较小的值,因为属于较少类别的样本可能数量上非常少。
树的最大深度(垂直深度):该超参数同样可以用来控制过拟合问题,较小的深度可以防止模型对特定的样本学习过于具体的关系,该超参数同样需要在验证集中调整。
叶结点的最大数量:叶结点的最大个数可以替代数的最大深度这一设定。因为生成一棵深度为 n 的二叉树,它所能产生的最大叶结点个数为
 。
。
分裂所需要考虑的最大特征数:即当我们搜索更好分离方案时所需要考虑的特征数量,我们常用的方法是取可用特征总数的平方根为最大特征数。
2、决策树的基本知识与代码实现
2.1 数据导入和清洗
为了展示不同的前文所述的决策树模型,我们将使用 Kaggle 上的美国收入数据集,我们都可以在 Kaggle.com 上下载该数据集。下面的代码可以展示该数据集的导入过程和部分内容:
importpandas as pd
importnumpy as np
fromplotnine import *
importmatplotlib.pyplot as plt
fromsklearn.preprocessing import LabelEncoder
fromsklearn_pandas import DataFrameMapper
fromsklearn.tree import DecisionTreeClassifier
fromsklearn.ensemble import RandomForestClassifier
training_data= './adult-training.csv'
test_data= './adult-test.csv'
columns=['Age','Workclass','fnlgwt','Education','EdNum','MaritalStatus','Occupation','Relationship','Race','Sex','CapitalGain','CapitalLoss','HoursPerWeek','Country','Income']
df_train_set= pd.read_csv(training_data, names=columns)
df_test_set= pd.read_csv(test_data, names=columns, skiprows=1)
df_train_set.drop('fnlgwt',axis=1, inplace=True)
df_test_set.drop('fnlgwt',axis=1, inplace=True)在上面的代码中,我们首先需要导入所有需要的库和模块,然后再读取数据和结构到训练数据和验证数据中。我们同样去除 fnlgwt 列,因为该数据行对于模型的训练并不重要。
输入以下语句可以看到训练数据的前五行:
df_train_set.head()如下所示,我们还需要做一些数据清洗。我们需要将所有列的的特殊字符移除,此外任何空格或者「.」都需要移除。
#replacethe special character to "Unknown"for i indf_train_set.columns:
df_train_set[i].replace('?', 'Unknown', inplace=True)
df_test_set[i].replace('?', 'Unknown', inplace=True)for col in df_train_set.columns:ifdf_train_set[col].dtype != 'int64':
df_train_set[col]= df_train_set[col].apply(lambda val: val.replace(" ", ""))
df_train_set[col]= df_train_set[col].apply(lambda val: val.replace(".", ""))
df_test_set[col]= df_test_set[col].apply(lambda val: val.replace(" ", ""))
df_test_set[col]= df_test_set[col].apply(lambda val: val.replace(".", ""))正如上图所示,有两行描述了个人的教育:Eduction 和 EdNum。我们假设这两个特征十分相关,因此我们可以移除 Education 列。Country 列对预测收入并不会起到什么作用,所以我们需要移除它。
df_train_set.drop(["Country","Education"], axis=1, inplace=True)
df_test_set.drop(["Country","Education"], axis=1, inplace=True)Age 和 EdNum 列是数值型的,我们可以将连续数值型转化为更高效的方式,例如将年龄换为 10 年的整数倍,教育年限换为 5 年的整数倍,实现的代码如下:
colnames= list(df_train_set.columns)
colnames.remove('Age')
colnames.remove('EdNum')
colnames= ['AgeGroup', 'Education'] + colnames
labels= ["{0}-{1}".format(i, i + 9) for i in range(0, 100, 10)]
df_train_set['AgeGroup']= pd.cut(df_train_set.Age, range(0, 101, 10), right=False,labels=labels)
df_test_set['AgeGroup']= pd.cut(df_test_set.Age, range(0, 101, 10), right=False,labels=labels)
labels= ["{0}-{1}".format(i, i + 4) for i in range(0, 20, 5)]
df_train_set['Education']= pd.cut(df_train_set.EdNum, range(0, 21, 5), right=False,labels=labels)
df_test_set['Education']= pd.cut(df_test_set.EdNum, range(0, 21, 5), right=False,labels=labels)
df_train_set= df_train_set[colnames]
df_test_set= df_test_set[colnames]现在我们已经清理了数据,下面语句可以展示我们数据的概况:
df_train_set.Income.value_counts()
<=50K
24720
>50K 7841
Name: Income, dtype:
int64
df_test_set.Income.value_counts()
<=50K
12435
>50K 3846
Name: Income, dtype: int64在训练集和测试集中,我们发现 <=50K 的类别要比>50K 的多 3 倍。从这里我们就可以看出来样本数据并不是均衡的数据,但是在这里为了简化问题,我们在这里将该数据集看作常规问题。
2.2 EDA
现在,让我们以图像的形式看一下训练数据中的不同特征的分布和相互依存(inter-dependence)关系。首先看一下关系(Relationships)和婚姻状况(MaritalStatus)特征是如何相互关联的。
(ggplot(df_train_set,aes(x = "Relationship", fill = "MaritalStatus"))+geom_bar(position="fill")+ theme(axis_text_x =element_text(angle = 60, hjust = 1)))让我们首先看一下不同年龄组中,教育对收入的影响(用受教育的年数进行衡量)。
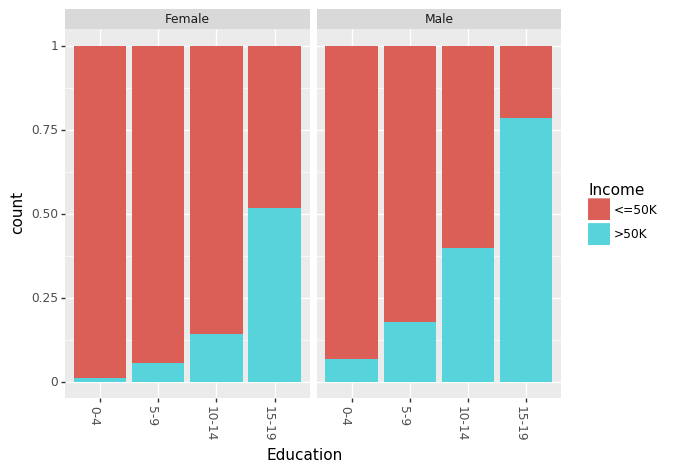
(ggplot(df_train_set,aes(x = "Education", fill = "Income"))+geom_bar(position="fill")+ theme(axis_text_x =element_text(angle = 60, hjust = 1))+ facet_wrap('~AgeGroup'))最近,有很多关于性别对收入差距的影响的相关说法。我们可以分别看见男性和女性的教育程度和种族间的影响。
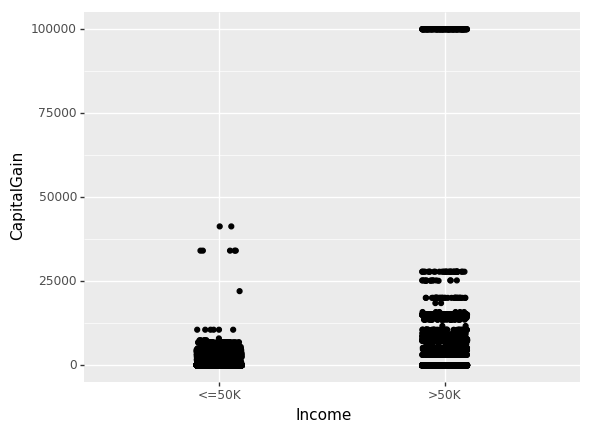
(ggplot(df_train_set,aes(x = "Education", fill = "Income"))+geom_bar(position="fill")+ theme(axis_text_x =element_text(angle = -90, hjust = 1))+ facet_wrap('~Sex'))(ggplot(df_train_set,aes(x = "Race", fill = "Income"))+geom_bar(position="fill")+ theme(axis_text_x =element_text(angle = -90, hjust = 1))+ facet_wrap('~Sex'))直到现在,我们仅关注了非数值特征(non-numeric)的相互关系。现在我们看一下资本收益(CapitalGain)和资本损失(CapitalLoss)对收入的影响。
(ggplot(df_train_set,aes(x="Income", y="CapitalGain"))+geom_jitter(position=position_jitter(0.1)))(ggplot(df_train_set,aes(x="Income", y="CapitalLoss"))+geom_jitter(position=position_jitter(0.1)))2.3 决策树的代码实现
现在我们理解了我们数据中的一些关系,所以就可以使用 sklearn.tree.DecisionTreeClassifier 创建一个简单的树分类器模型。然而,为了使用这一模型,我们需要把所有我们的非数值数据转化成数值型数据。我们可以直接在 Pandas 数据框架中使用 sklearn.preprocessing.LabeEncoder 模块和 sklearn_pandas 模块就可以轻松地完成这一步骤。
mapper= DataFrameMapper([('AgeGroup', LabelEncoder()),('Education',LabelEncoder()),('Workclass', LabelEncoder()),('MaritalStatus',LabelEncoder()),('Occupation', LabelEncoder()),('Relationship',LabelEncoder()),('Race', LabelEncoder()),('Sex',LabelEncoder()),('Income', LabelEncoder())], df_out=True,default=None)
cols= list(df_train_set.columns)
cols.remove("Income")
cols= cols[:-3] + ["Income"] + cols[-3:]
df_train= mapper.fit_transform(df_train_set.copy())
df_train.columns= cols
df_test= mapper.transform(df_test_set.copy())
df_test.columns= cols
cols.remove("Income")
x_train,y_train = df_train[cols].values, df_train["Income"].values
x_test,y_test = df_test[cols].values, df_test["Income"].values现在我们用正确的形式对数据进行了训练和测试,已创建了我们的第一个模型!
treeClassifier= DecisionTreeClassifier()
treeClassifier.fit(x_train,y_train)
treeClassifier.score(x_test,y_test)最简单的且没有优化的概率分类器模型可以达到 83.5% 的精度。在分类问题中,混淆矩阵(confusion matrix)是衡量模型精度的好方法。使用下列代码我们可以绘制任意基于树的模型的混淆矩阵。
importitertoolsfrom sklearn.metrics import confusion_matrixdefplot_confusion_matrix(cm, classes, normalize=False):"""
Thisfunction prints and plots the confusion matrix.
Normalizationcan be applied by setting `normalize=True`.
"""
cmap= plt.cm.Blues
title= "Confusion Matrix"if normalize:
cm= cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
cm= np.around(cm, decimals=3)
plt.imshow(cm,interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks= np.arange(len(classes))
plt.xticks(tick_marks,classes, rotation=45)
plt.yticks(tick_marks,classes)
thresh= cm.max() / 2.for i, j in itertools.product(range(cm.shape[0]),range(cm.shape[1])):
plt.text(j,i, cm[i, j],
horizontalalignment="center",
color="white"if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('Truelabel')
plt.xlabel('Predictedlabel')现在,我们可以看到第一个模型的混淆矩阵:
y_pred= treeClassifier.predict(x_test)
cfm= confusion_matrix(y_test, y_pred, labels=[0, 1])
plt.figure(figsize=(10,6))
plot_confusion_matrix(cfm,classes=["<=50K", ">50K"], normalize=True)我们发现多数类别(<=50K)的精度为 90.5%,少数类别(>50K)的精度只有 60.8%。
让我们看一下调校此简单分类器的方法。我们能使用带有 5 折交叉验证的 GridSearchCV() 来调校树分类器的各种重要参数。
fromsklearn.model_selection import GridSearchCV
parameters =
{'max_features':(None, 9, 6),'max_depth':(None, 24,
16),'min_samples_split': (2, 4, 8),'min_samples_leaf': (16, 4,
12)}
clf = GridSearchCV(treeClassifier, parameters, cv=5,
n_jobs=4)
clf.fit(x_train, y_train)
clf.best_score_,
clf.score(x_test, y_test), clf.best_params_
(0.85934092933263717,
0.85897672133161351,
{'max_depth': 16,
'max_features':
9,
'min_samples_leaf': 16,
'min_samples_split': 8})经过优化,我们发现精度上升到了 85.9%。在上方,我们也可以看见最优模型的参数。现在,让我们看一下 已优化模型的混淆矩阵(confusion matrix):
y_pred= clf.predict(x_test)
cfm= confusion_matrix(y_test, y_pred, labels=[0, 1])
plt.figure(figsize=(10,6))
plot_confusion_matrix(cfm,classes=["<=50K", ">50K"], normalize=True)经过优化,我们发现在两种类别下,预测精度都有所提升。
三、随机森林
1.随机森林简介
有了决策树的基本知识,我们就可以来学习随机森林算法了
随机森林由决策树组成,决策树实际上是将空间用超平面进行划分的一种方法,每次分割的时候,都将当前的空间一分为二。
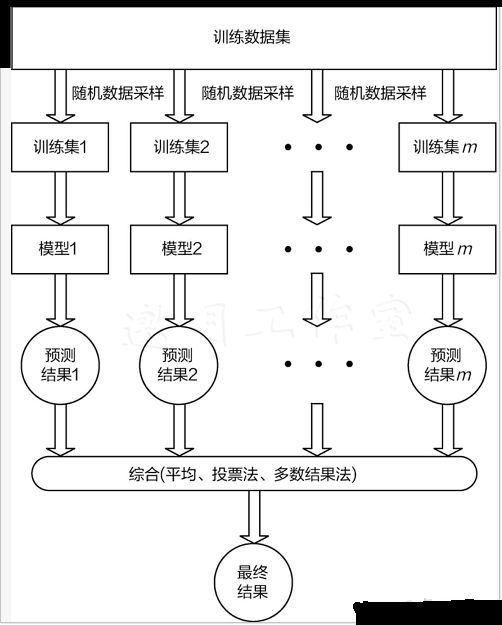
随机森林的构造过程:
1.假如有N个样本,则有放回的随机选择N个样本(每次随机选择一个样本,然后返回继续选择)。这选择好了的N个样本用来训练一个决策树,作为决策树根节点处的样本。
2.当每个样本有M个属性时,在决策树的每个节点需要分裂时,随机从这M个属性中选取出m个属性,满足条件m<< M。然后从这m个属性中采用某种策略(比如说信息增益)来选择1个属性作为该节点的分裂属性。
3.决策树形成过程中每个节点都要按照步骤2来分裂(很容易理解,如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性,则该节点已经达到了叶子节点,无须继续分裂了)。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
4.按照步骤1~3建立大量的决策树,这样就构成了随机森林了。
在建立每一棵决策树的过程中,有两点需要注意采样与完全分裂。
首先是两个随机采样的过程,randomforest对输入的数据要进行行、列的采样。对于行采样,采用有放回的方式,也就是在采样得到的样本集合中,可能有重复的样本。假设输入样本为N个,那么采样的样本也为N个。这样使得在训练的时候,每一棵树的输入样本都不是全部的样本,使得相对不容易出现over-fitting。然后进行列采样,从M个feature中,选择m个(m<< M)。
之后就是对采样之后的数据使用完全分裂的方式建立出决策树,这样决策树的某一个叶子节点要么是无法继续分裂的,要么里面的所有样本的都是指向的同一个分类。一般很多的决策树算法都一个重要的步骤——剪枝,但是这里不这样干,由于之前的两个随机采样的过程保证了随机性,所以就算不剪枝,也不会出现over-fitting。
通过分类,子集合的熵要小于未分类前的状态,这就带来了信息增益(informationgain)
2.随机森林和决策树的对比
决策树有很多的优点:
a.在数据集上表现良好,两个随机性的引入,使得随机森林不容易陷入过拟合
b.在当前的很多数据集上,相对其他算法有着很大的优势,两个随机性的引入,使得随机森林具有很好的抗噪声能力
c.它能够处理很高维度(feature很多)的数据,并且不用做特征选择,对数据集的适应能力强:既能处理离散型数据,也能处理连续型数据,数据集无需规范化
d.可生成一个Proximities=(pij)矩阵,用于度量样本之间的相似性:pij=aij/N,aij表示样本i和j出现在随机森林中同一个叶子结点的次数,N随机森林中树的颗数
e.在创建随机森林的时候,对generlizationerror使用的是无偏估计
f. 训练速度快,可以得到变量重要性排序(两种:基于OOB误分率的增加量和基于分裂时的GINI下降量
g.在训练过程中,能够检测到feature间的互相影响
h. 容易做成并行化方法
i.实现比较简单
随机森林主要应用于回归和分类。本文主要探讨基于随机森林的分类问题。随机森林和使用决策树作为基本分类器的(bagging)有些类似。以决策树为基本模型的bagging在每次bootstrap放回抽样之后,产生一棵决策树,抽多少样本就生成多少棵树,在生成这些树的时候没有进行更多的干预。而随机森林也是进行bootstrap抽样,但它与bagging的区别是:在生成每棵树的时候,每个节点变量都仅仅在随机选出的少数变量中产生。因此,不但样本是随机的,连每个节点变量(Features)的产生都是随机的。
许多研究表明,组合分类器比单一分类器的分类效果好,随机森林(randomforest)是一种利用多个分类树对数据进行判别与分类的方法,它在对数据进行分类的同时,还可以给出各个变量(基因)的重要性评分,评估各个变量在分类中所起的作用。
随机森林算法得到的随机森林中的每一棵都是很弱的,但是大家组合起来就很厉害了。我觉得可以这样比喻随机森林算法:每一棵决策树就是一个精通于某一个窄领域的专家(因为我们从M个feature中选择m让每一棵决策树进行学习),这样在随机森林中就有了很多个精通不同领域的专家,对一个新的问题(新的输入数据),可以用不同的角度去看待它,最终由各个专家,投票得到结果。而这正是群体智慧(swarmintelligence),经济学上说的看不见的手,也是这样一个分布式的分类系统,由每一自己子领域里的专家,利用自己独有的默会知识,去对一项产品进行分类,决定是否需要生产。随机森林的效果取决于多个分类树要相互独立,要想经济持续发展,不出现overfiting(就是由政府主导的经济增长,但在遇到新情况后产生泡沫),我们就需要要企业独立发展,独立选取自己的feature。
3.随机森林的代码实现
代码实现流程:
(1)导入文件并将所有特征转换为float形式
(2)将数据集分成n份,方便交叉验证
(3)构造数据子集(随机采样),并在指定特征个数(假设m个,手动调参)下选取最优特征
(4)构造决策树
(5)创建随机森林(多个决策树的结合)
(6)输入测试集并进行测试,输出预测结果
#-*- coding: utf-8 -*-
importcsv
fromrandom import seed
fromrandom import randrange
frommath import sqrt
defloadCSV(filename):#加载数据,一行行的存入列表
dataSet= []
withopen(filename, 'r') as file:
csvReader= csv.reader(file)
forline in csvReader:
dataSet.append(line)
returndataSet
#除了标签列,其他列都转换为float类型
defcolumn_to_float(dataSet):
featLen= len(dataSet[0]) - 1
fordata in dataSet:
forcolumn in range(featLen):
data[column]= float(data[column].strip())
#将数据集随机分成N块,方便交叉验证,其中一块是测试集,其他四块是训练集
defspiltDataSet(dataSet, n_folds):
fold_size= int(len(dataSet) / n_folds)
dataSet_copy= list(dataSet)
dataSet_spilt= []
fori in range(n_folds):
fold= []
whilelen(fold) < fold_size: # 这里不能用if,if只是在第一次判断时起作用,while执行循环,直到条件不成立
index= randrange(len(dataSet_copy))
fold.append(dataSet_copy.pop(index)) # pop() 函数用于移除列表中的一个元素(默认最后一个元素),并且返回该元素的值。
dataSet_spilt.append(fold)
returndataSet_spilt
#构造数据子集
defget_subsample(dataSet, ratio):
subdataSet= []
lenSubdata= round(len(dataSet) * ratio)#返回浮点数
whilelen(subdataSet) < lenSubdata:
index= randrange(len(dataSet) - 1)
subdataSet.append(dataSet[index])
#print len(subdataSet)
returnsubdataSet
#分割数据集
defdata_spilt(dataSet, index, value):
left= []
right= []
forrow in dataSet:
ifrow[index] < value:
left.append(row)
else:
right.append(row)
returnleft, right
#计算分割代价
defspilt_loss(left, right, class_values):
loss= 0.0
forclass_value in class_values:
left_size= len(left)
ifleft_size != 0: # 防止除数为零
prop= [row[-1] for row in left].count(class_value) / float(left_size)
loss+= (prop * (1.0 - prop))
right_size= len(right)
ifright_size != 0:
prop= [row[-1] for row in right].count(class_value) / float(right_size)
loss+= (prop * (1.0 - prop))
returnloss
#选取任意的n个特征,在这n个特征中,选取分割时的最优特征
defget_best_spilt(dataSet, n_features):
features= []
class_values= list(set(row[-1] for row in dataSet))
b_index,b_value, b_loss, b_left, b_right = 999, 999, 999, None, None
whilelen(features) < n_features:
index= randrange(len(dataSet[0]) - 1)
ifindex not in features:
features.append(index)
#print 'features:',features
forindex in features:#找到列的最适合做节点的索引,(损失最小)
forrow in dataSet:
left,right = data_spilt(dataSet, index, row[index])#以它为节点的,左右分支
loss= spilt_loss(left, right, class_values)
ifloss < b_loss:#寻找最小分割代价
b_index,b_value, b_loss, b_left, b_right = index, row[index], loss, left,right
#print b_loss
#print type(b_index)
return{'index': b_index, 'value': b_value, 'left': b_left, 'right':b_right}
#决定输出标签
defdecide_label(data):
output= [row[-1] for row in data]
returnmax(set(output), key=output.count)
#子分割,不断地构建叶节点的过程
defsub_spilt(root, n_features, max_depth, min_size, depth):
left= root['left']
#print left
right= root['right']
del(root['left'])
del(root['right'])
#print depth
ifnot left or not right:
root['left']= root['right'] = decide_label(left + right)
#print 'testing'
return
ifdepth > max_depth:
root['left']= decide_label(left)
root['right']= decide_label(right)
return
iflen(left) < min_size:
root['left']= decide_label(left)
else:
root['left']= get_best_spilt(left, n_features)
#print 'testing_left'
sub_spilt(root['left'],n_features, max_depth, min_size, depth + 1)
iflen(right) < min_size:
root['right']= decide_label(right)
else:
root['right']= get_best_spilt(right, n_features)
#print 'testing_right'
sub_spilt(root['right'],n_features, max_depth, min_size, depth + 1)
#构造决策树
defbuild_tree(dataSet, n_features, max_depth, min_size):
root= get_best_spilt(dataSet, n_features)
sub_spilt(root,n_features, max_depth, min_size, 1)
returnroot
#预测测试集结果
defpredict(tree, row):
predictions= []
ifrow[tree['index']] < tree['value']:
ifisinstance(tree['left'], dict):
returnpredict(tree['left'], row)
else:
returntree['left']
else:
ifisinstance(tree['right'], dict):
returnpredict(tree['right'], row)
else:
returntree['right']
#predictions=set(predictions)
defbagging_predict(trees, row):
predictions= [predict(tree, row) for tree in trees]
returnmax(set(predictions), key=predictions.count)
#创建随机森林
defrandom_forest(train, test, ratio, n_feature, max_depth, min_size,n_trees):
trees= []
fori in range(n_trees):
train= get_subsample(train, ratio)#从切割的数据集中选取子集
tree= build_tree(train, n_features, max_depth, min_size)
#print 'tree %d: '%i,tree
trees.append(tree)
#predict_values = [predict(trees,row) for row in test]
predict_values= [bagging_predict(trees, row) for row in test]
returnpredict_values
#计算准确率
defaccuracy(predict_values, actual):
correct= 0
fori in range(len(actual)):
ifactual[i] == predict_values[i]:
correct+= 1
returncorrect / float(len(actual))
if__name__ == '__main__':
seed(1)
dataSet= loadCSV('C:/Users/shadow/Desktop/组会/sonar-all-data.csv')
column_to_float(dataSet)#dataSet
n_folds= 5
max_depth= 16
min_size= 1
ratio= 1.0
#n_features=sqrt(len(dataSet)-1)
n_features= 15
n_trees= 11
folds= spiltDataSet(dataSet, n_folds)#先是切割数据集
scores= []
forfold in folds:
train_set= folds[
:]
#此处不能简单地用train_set=folds,这样用属于引用,那么当train_set的值改变的时候,folds的值也会改变,所以要用复制的形式。(L[:])能够复制序列,D.copy()能够复制字典,list能够生成拷贝list(L)
train_set.remove(fold)#选好训练集
#print len(folds)
train_set= sum(train_set, []) # 将多个fold列表组合成一个train_set列表
#print len(train_set)
test_set= []
forrow in fold:
row_copy= list(row)
row_copy[-1]= None
test_set.append(row_copy)
#for row in test_set:
#print row[-1]
actual= [row[-1] for row in fold]
predict_values= random_forest(train_set, test_set, ratio, n_features, max_depth,min_size, n_trees)
accur= accuracy(predict_values, actual)
scores.append(accur)
print('Trees is %d' % n_trees)
print('scores:%s' % scores)
print('mean score:%s' % (sum(scores) / float(len(scores))))
#-*- coding: utf-8 -*-
importcsv
fromrandom import seed
fromrandom import randrange
frommath import sqrt
defloadCSV(filename):#加载数据,一行行的存入列表
dataSet= []
withopen(filename, 'r') as file:
csvReader= csv.reader(file)
forline in csvReader:
dataSet.append(line)
returndataSet
#除了标签列,其他列都转换为float类型
defcolumn_to_float(dataSet):
featLen= len(dataSet[0]) - 1
fordata in dataSet:
forcolumn in range(featLen):
data[column]= float(data[column].strip())
#将数据集随机分成N块,方便交叉验证,其中一块是测试集,其他四块是训练集
defspiltDataSet(dataSet, n_folds):
fold_size= int(len(dataSet) / n_folds)
dataSet_copy= list(dataSet)
dataSet_spilt= []
fori in range(n_folds):
fold= []
whilelen(fold) < fold_size: # 这里不能用if,if只是在第一次判断时起作用,while执行循环,直到条件不成立
index= randrange(len(dataSet_copy))
fold.append(dataSet_copy.pop(index)) # pop() 函数用于移除列表中的一个元素(默认最后一个元素),并且返回该元素的值。
dataSet_spilt.append(fold)
returndataSet_spilt
#构造数据子集
defget_subsample(dataSet, ratio):
subdataSet= []
lenSubdata= round(len(dataSet) * ratio)#返回浮点数
whilelen(subdataSet) < lenSubdata:
index= randrange(len(dataSet) - 1)
subdataSet.append(dataSet[index])
#print len(subdataSet)
returnsubdataSet
#分割数据集
defdata_spilt(dataSet, index, value):
left= []
right= []
forrow in dataSet:
ifrow[index] < value:
left.append(row)
else:
right.append(row)
returnleft, right
#计算分割代价
defspilt_loss(left, right, class_values):
loss= 0.0
forclass_value in class_values:
left_size= len(left)
ifleft_size != 0: # 防止除数为零
prop= [row[-1] for row in left].count(class_value) / float(left_size)
loss+= (prop * (1.0 - prop))
right_size= len(right)
ifright_size != 0:
prop= [row[-1] for row in right].count(class_value) / float(right_size)
loss+= (prop * (1.0 - prop))
returnloss
#选取任意的n个特征,在这n个特征中,选取分割时的最优特征
defget_best_spilt(dataSet, n_features):
features= []
class_values= list(set(row[-1] for row in dataSet))
b_index,b_value, b_loss, b_left, b_right = 999, 999, 999, None, None
whilelen(features) < n_features:
index= randrange(len(dataSet[0]) - 1)
ifindex not in features:
features.append(index)
#print 'features:',features
forindex in features:#找到列的最适合做节点的索引,(损失最小)
forrow in dataSet:
left,right = data_spilt(dataSet, index, row[index])#以它为节点的,左右分支
loss= spilt_loss(left, right, class_values)
ifloss < b_loss:#寻找最小分割代价
b_index,b_value, b_loss, b_left, b_right = index, row[index], loss, left,right
#print b_loss
#print type(b_index)
return{'index': b_index, 'value': b_value, 'left': b_left, 'right':b_right}
#决定输出标签
defdecide_label(data):
output= [row[-1] for row in data]
returnmax(set(output), key=output.count)
#子分割,不断地构建叶节点的过程
defsub_spilt(root, n_features, max_depth, min_size, depth):
left= root['left']
#print left
right= root['right']
del(root['left'])
del(root['right'])
#print depth
ifnot left or not right:
root['left']= root['right'] = decide_label(left + right)
#print 'testing'
return
ifdepth > max_depth:
root['left']= decide_label(left)
root['right']= decide_label(right)
return
iflen(left) < min_size:
root['left']= decide_label(left)
else:
root['left']= get_best_spilt(left, n_features)
#print 'testing_left'
sub_spilt(root['left'],n_features, max_depth, min_size, depth + 1)
iflen(right) < min_size:
root['right']= decide_label(right)
else:
root['right']= get_best_spilt(right, n_features)
#print 'testing_right'
sub_spilt(root['right'],n_features, max_depth, min_size, depth + 1)
#构造决策树
defbuild_tree(dataSet, n_features, max_depth, min_size):
root= get_best_spilt(dataSet, n_features)
sub_spilt(root,n_features, max_depth, min_size, 1)
returnroot
#预测测试集结果
defpredict(tree, row):
predictions= []
ifrow[tree['index']] < tree['value']:
ifisinstance(tree['left'], dict):
returnpredict(tree['left'], row)
else:
returntree['left']
else:
ifisinstance(tree['right'], dict):
returnpredict(tree['right'], row)
else:
returntree['right']
#predictions=set(predictions)
defbagging_predict(trees, row):
predictions= [predict(tree, row) for tree in trees]
returnmax(set(predictions), key=predictions.count)
#创建随机森林
defrandom_forest(train, test, ratio, n_feature, max_depth, min_size,n_trees):
trees= []
fori in range(n_trees):
train= get_subsample(train, ratio)#从切割的数据集中选取子集
tree= build_tree(train, n_features, max_depth, min_size)
#print 'tree %d: '%i,tree
trees.append(tree)
#predict_values = [predict(trees,row) for row in test]
predict_values= [bagging_predict(trees, row) for row in test]
returnpredict_values
#计算准确率
defaccuracy(predict_values, actual):
correct= 0
fori in range(len(actual)):
ifactual[i] == predict_values[i]:
correct+= 1
returncorrect / float(len(actual))
if__name__ == '__main__':
seed(1)
dataSet= loadCSV('C:/Users/shadow/Desktop/组会/sonar-all-data.csv')
column_to_float(dataSet)#dataSet
n_folds= 5
max_depth= 16
min_size= 1
ratio= 1.0
#n_features=sqrt(len(dataSet)-1)
n_features= 15
n_trees= 11
folds= spiltDataSet(dataSet, n_folds)#先是切割数据集
scores= []
forfold in folds:
train_set= folds[
:]
#此处不能简单地用train_set=folds,这样用属于引用,那么当train_set的值改变的时候,folds的值也会改变,所以要用复制的形式。(L[:])能够复制序列,D.copy()能够复制字典,list能够生成拷贝list(L)
train_set.remove(fold)#选好训练集
#print len(folds)
train_set= sum(train_set, []) # 将多个fold列表组合成一个train_set列表
#print len(train_set)
test_set= []
forrow in fold:
row_copy= list(row)
row_copy[-1]= None
test_set.append(row_copy)
#for row in test_set:
#print row[-1]
actual= [row[-1] for row in fold]
predict_values= random_forest(train_set, test_set, ratio, n_features, max_depth,min_size, n_trees)
accur= accuracy(predict_values, actual)
scores.append(accur)
print('Trees is %d' % n_trees)
print('scores:%s' % scores)
print('mean score:%s' % (sum(scores) / float(len(scores))))