贝叶斯定理

1.贝叶斯定理

贝叶斯定理：$P(H|X)=\frac{P(X|H)P(H)}{P(X)}$

以上是一个特征的例子，如果特征多个的情况下会使得统计量巨大如下图所示的一组数据，如果需要计算办证对于垃圾邮件的影响，则需要计算办证+理财堆垃圾邮件的影响，办证+理财+投资对垃圾邮件的影响，计算办证+理财+投资+资讯对垃圾邮件的影响…… 总共需要计算$2^{n-1}$次，n是特征数。这样如果我们有很多特征的话，显然是无法完成计算的。

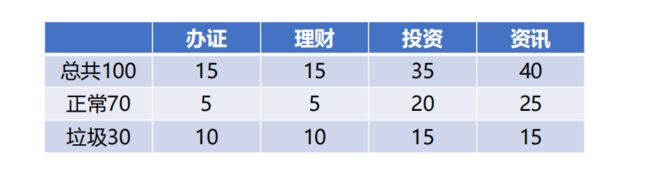
于是我们引入了朴素贝叶斯，假设X1，X2，X3……之间都是相互独立的
$$P(H|X)=\frac{P(X1|H)P(X2|H)\dots \dots P(Xn|H)P(H)}{P(X1)P(X2)\dots \dots P(Xn)}$$
但是显然各个特征之间不是相互独立的。就以上边的四个特征来说，投资和理财之间肯定不是相互独立的，投资可以说是理财的一种方式。但是由于我们假设相互独立计算出来的结果误差较小，就认为采用朴素贝叶斯来计算了。

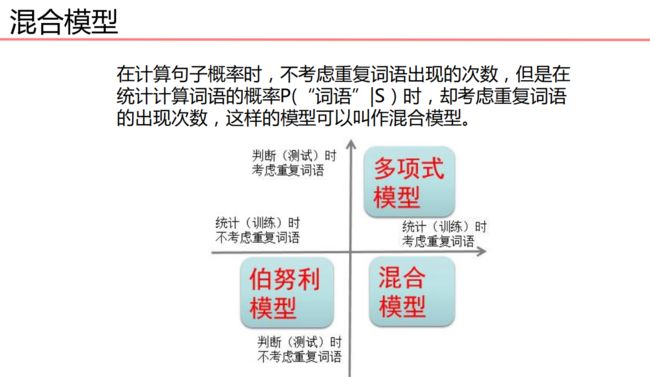
2.集中贝叶斯模型

2.词袋模型

词袋模型（Bag of Words model(Bow model)最早出现在自然语言处理和信息检索领域。该模型忽略掉文本的语法和语序等要素，将其仅仅看作是若干个词汇的集合，文档中每个单词的出现都是独立的。Bow使用一组无序单词来表达一段文字或一个文档

通过词袋模型将不同长度的文章转换成相同长度的向量。

CountVectorize方法来构建单词的字典，每个单词实例被转换为一个特征向量的一个数值特征，每个元素是特定单词在文本中出现的次数

from sklearn.feature_extraction.text import CountVectorizer

texts=['dog cat finsih','dog fish dog','bird','monkey,dog']
model=CountVectorizer()
model_fit=model.fit_transform(texts)

print(model_fit)
print(model.get_feature_names_out())
print(model_fit.toarray())
print(model_fit.toarray().sum(axis=0))#列方向相加

  (0, 2)	1
  (0, 1)	1
  (0, 3)	1
  (1, 2)	2
  (1, 4)	1
  (2, 0)	1
  (3, 2)	1
  (3, 5)	1
['bird' 'cat' 'dog' 'finsih' 'fish' 'monkey']
[[0 1 1 1 0 0]
 [0 0 2 0 1 0]
 [1 0 0 0 0 0]
 [0 0 1 0 0 1]]
[1 1 4 1 1 1]

3.TF——IDF

提取文章关键字：
1.提取词频(Term Frequency，缩写TF).一篇文章中出现最多的词可能是“的，是，在”等对文章分类或者搜索没有帮助的停用词(stop words).
2.假设我们吧停用词都过滤掉了，只考虑有意义的词。可能会遇到这样一个问题，“中国”，“蜜蜂”，“养殖”这三个词的TF一样，作为关键词，他们的重要性是一样的吗？
3.显然不是这样。“中国”是很常见的词，相对而言，“蜜蜂”和“养殖”不是那么常见。如果这三个词在一篇文章中出现的次数一样多，有理由认为，“蜜蜂”和“养殖”的重要性大于“中国”，在关键词排序上“养殖”和“蜜蜂”应该排在中国的前面。
所以我们需要一个重要性调整系数，衡量一个词是不是常见词。如果某个词比较少见，但它在这篇文章出现多次，那么他很可能就反应了这篇文章的特性，正是我们需要的关键词。

用统计学语言表达，就是在词频的基础上，要对每个词分配一个“重要性”权重，最常见的词“的，是，在”给予最小的权重，较常见的词“中国”给予较小的权重。较少见的 词“蜜蜂”，“养殖”给予较大的权重。这个权重叫做“逆文档频率”(Inverse Document Frequency)，缩写为IDF，他的大小与一个词的常见程度成反比。
计算词频的方法：

from sklearn.feature_extraction.text import TfidfVectorizer

text=['dog bird','dog cat','the ','fox']
model_tif=TfidfVectorizer(norm=None)#将norm设置为none计算结果就会和上边的图片一样
model_tif.fit(text)

print(model_tif.vocabulary_)
print(model_tif.idf_)#计算IDF 向量个元素位置序号与字典值对应
vector=model_tif.fit_transform(text)#计算RF-IDF
print(vector.toarray())

{'dog': 2, 'bird': 0, 'cat': 1, 'the': 4, 'fox': 3}
[1.91629073 1.91629073 1.51082562 1.91629073 1.91629073]
[[1.91629073 0.         1.51082562 0.         0.        ]
 [0.         1.91629073 1.51082562 0.         0.        ]
 [0.         0.         0.         0.         1.91629073]
 [0.         0.         0.         1.91629073 0.        ]]