机器学习—决策树

• 从根节点开始一步一步走到叶子节点（决策）
• 所有的数据最终都会落到叶子节点，既可以做分类也可以做回归

根节点的决策应较强。

• 树的组成

根节点：第一个节点

非叶子结点与分支：中间过程

叶子结点：最终的决策结果

• 决策树的训练与测试

训练阶段：从给定的训练集构造出来一棵树（从根节点开始选择合适的特征，按优先级进行排列）

测试阶段：根据构造出来的树模型从上到下走一遍

• 如何切分特征（选择节点）

问题：根节点的选择该用哪个特征？接下来如何切分？

应该根据分类效果来排列先后顺序。

目标：通过一种衡量标准，来计算通过不同特征进行分支选择后的分类情况，找出来最好的那个当成根节点，以此类推。

• 熵

表示随机变量不确定性的度量，即物体内部的混乱程度。

$$\begin{gathered} H(X)=-\sum pi\ast logpi,i=1,2,...,n \\ pi为概率，当概率越大时，熵值越小 \end{gathered}$$

如：$A=\{1,1,1,1,1,1,1,2,2\}$，$ B = {1,2,3,4,5,6,7,8,9}$

A集合中的类别少，熵值低；B集合中类别多，熵值高。

在分类任务中，通过节点分支后数据类别的熵值越小为好。

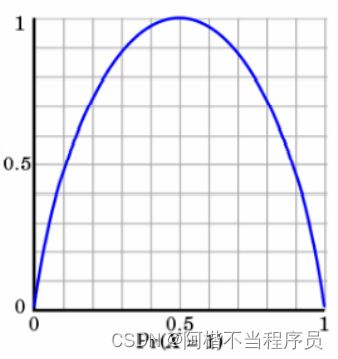
如图，不确定性越大，得到的熵值也就越大：

当p=0或p=1时，$H(p)=0$，随机变量完全没有不确定性。

当p=0.5时，$H(p)=1$，此时随机变量的不确定性最大。

• 信息增益

表示特征X使得类Y的不确定性减少的程度。

选择信息增益高的作为优先节点。

• 决策树算法

ID3：信息增益

C4.5：信息增益率（解决ID3问题，考虑自身熵）

CART：使用GINI系数来当做衡量标准

GINI系数：$Gini(p)={\sum }_{k=1}^k{p}_k(1-p_k)=1-{\sum }_{k=1}^k{p}_k^2$

• 连续值怎么办？

连续值离散化：对数据进行排序，然后选取分界点（若为二分类）。

$60,70,75,85,90,95,100,120,125,220$

如：$60|70,75,85,90,95,100,120,125,220$，将60作为分界点，计算熵值；

$60,70|75,85,90,95,100,120,125,220$，将70作为分界点，计算熵值；

依次切分，比较即可得。

• 剪枝策略（避免过拟合）

决策树过拟合风险很大，理论上可以完全分得开数据。

将数据分支到极致，即分到结点只有一个样本，就造成了过拟合。

预剪枝：边建立决策树边进行剪枝的操作（更实用）。

限制深度（选取的特征个数）、叶子结点个数、叶子结点样本数、信息增益量等。

控制决策树的规模和复杂程度。

后剪枝：当建立完成决策树后来进行剪枝操作。

通过一定的衡量标准，$C_{\alpha }(T)=C(T)+\alpha \cdot |T_{leaf}|$（损失=熵值+平衡系数*叶子结点个数）

• 回归问题

利用方差来比较连续值的划分。

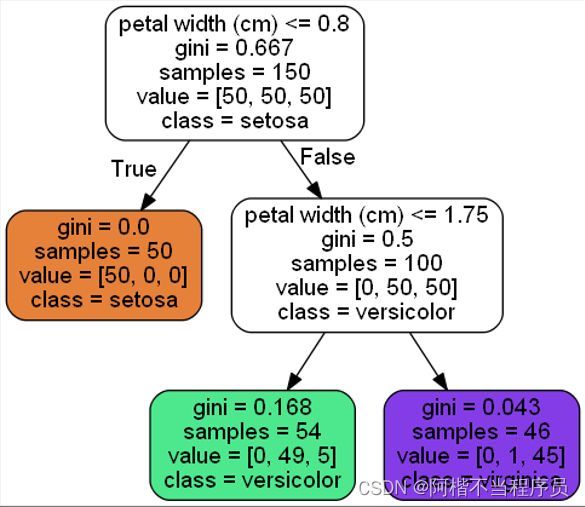
树模型可视化展示

• 用莺尾花数据集进行展示

# 导入数据集和模型
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

iris = load_iris()
X = iris.data[:,2:] # 选择2,3列数据
y = iris.target

tree_clf = DecisionTreeClassifier(max_depth=2) # 最大深度
tree_clf.fit(X,y)

# 生成决策树模型的图片
from sklearn.tree import export_graphviz

export_graphviz(
    tree_clf, # 模型
    out_file = "iris_tree.dot",
    feature_names = iris.feature_names[2:], # 特征名
    class_names = iris.target_names, # y值的名字
    rounded = True,
    filled = True
)

会生成一个.dot的文件，然后用此命令，转为png文件：

dot -Tpng iris_tree.dot -o iris_tree.png

# 图片展示
from IPython.display import Image
Image(filename='iris_tree.png',width=400,height=400)

决策边界展示

from matplotlib.colors import ListedColormap

def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
    x1s = np.linspace(axes[0], axes[1], 100) # 构造特征
    x2s = np.linspace(axes[2], axes[3], 100)
    x1, x2 = np.meshgrid(x1s, x2s) # 棋盘
    X_new = np.c_[x1.ravel(), x2.ravel()] # 测试集
    y_pred = clf.predict(X_new).reshape(x1.shape) # 预测值
    custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
    plt.contourf(x1, x2, y_pred, alpha=0.3, cmap=custom_cmap)
    if not iris:
        custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
        plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
    if plot_training: # 画图：训练数据
        plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris-Setosa")
        plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris-Versicolor")
        plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", label="Iris-Virginica")
        plt.axis(axes)
    if iris:
        plt.xlabel("Petal length", fontsize=14)
        plt.ylabel("Petal width", fontsize=14)
    else:
        plt.xlabel(r"$x_1$", fontsize=18)
        plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
    if legend:
        plt.legend(loc="lower right", fontsize=14)

plt.figure(figsize=(8, 4))
plot_decision_boundary(tree_clf, X, y)
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2) # 分割线
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2) 
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.40, 1.0, "Depth=0", fontsize=15)
plt.text(3.2, 1.80, "Depth=1", fontsize=13)
plt.text(4.05, 0.5, "(Depth=2)", fontsize=11)
plt.title('Decision Tree decision boundaries')

plt.show()

概率估计

• 通过输入特征值，获取概率值或预测值

# 预测概率值
tree_clf.predict_proba([[5,1.5]]) # 分别返回属于三个类别的概率
# array([[0.        , 0.90740741, 0.09259259]])

# 预测值
tree_clf.predict([[5,1.5]])
# array([1])

输入数据为：花瓣长5厘米，宽1.5厘米的花。

相应的叶节点是深度为2的左节点，因此决策树应输出以下概率：

• Iris-Setosa 为 0％（0/54），
• Iris-Versicolor 为 90.7％（49/54），
• Iris-Virginica 为 9.3％（5/54）。

最终预测值为1分类。

决策树中的正则化

• DecisionTreeClassifier参数：

min_samples_split：节点在分割之前最小样本数

min_samples_leaf：叶子节点最小样本数

max_leaf_nodes：叶子节点的最多个数（$n_0$）

max_features：在每个节点处评估用于拆分的最大特征数

max_depth：树最大的深度

• 对比实验

# 导入数据集
from sklearn.datasets import make_moons
X,y = make_moons(n_samples=100,noise=0.25,random_state=53)
tree_clf1 = DecisionTreeClassifier(random_state=42)
tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4,random_state=42)
# 训练
tree_clf1.fit(X,y)
tree_clf2.fit(X,y)


plt.figure(figsize=(12,4))
plt.subplot(121)
plot_decision_boundary(tree_clf1,X,y,axes=[-1.5,2.5,-1,1.5],iris=False)
plt.title('No restriction')

plt.subplot(122)
plot_decision_boundary(tree_clf2,X,y,axes=[-1.5,2.5,-1,1.5],iris=False)
plt.title('min_samples_leaf=4')

左图不做限制时，决策边界较为复杂，且右下角黄点，明显的形成了过拟合；

而限制了叶子结点最小样本数后，效果改善。

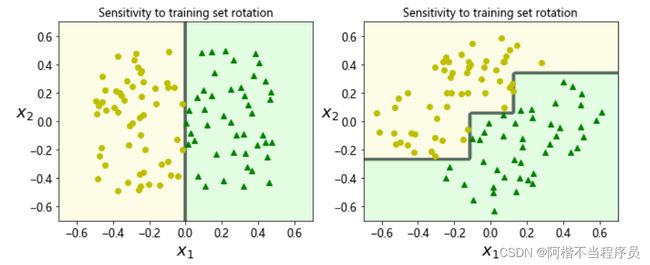
对数据的敏感

• 将数据集进行旋转之后的效果

# 构造数据集
np.random.seed(6)
Xs = np.random.rand(100,2) - 0.5
ys = (Xs[:,0] > 0).astype(np.float32) * 2

# 旋转角度
angle = np.pi/4
# 旋转矩阵
rotation_matrix = np.array([[np.cos(angle),-np.sin(angle)],[np.sin(angle),np.cos(angle)]])
# 旋转数据集
Xsr = Xs.dot(rotation_matrix)

# 原始数据集
tree_clf_s = DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs,ys)
# 旋转后数据集
tree_clf_sr = DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr,ys)

# 画图
plt.figure(figsize=(11,4))
plt.subplot(121)
plot_decision_boundary(tree_clf_s,Xs,ys,axes=[-0.7,0.7,-0.7,0.7],iris=False)
plt.title('Sensitivity to training set rotation')

plt.subplot(122)
plot_decision_boundary(tree_clf_sr,Xsr,ys,axes=[-0.7,0.7,-0.7,0.7],iris=False)
plt.title('Sensitivity to training set rotation')

plt.show()

将数据集进行旋转之后，决策边界也会发生改变。

回归任务

• 决策树也能做回归的任务

# 构造数据集
np.random.seed(42)
m = 200
X = np.random.rand(m,1)
y = 4*(X-0.5)**2
y = y + np.random.randn(m,1)/10 # 高斯，数据分布抖动

# 导入决策树回归模型
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor(max_depth=2)
tree_reg.fit(X,y)

export_graphviz(
    tree_reg,
    out_file=("regression_tree.dot"),
    feature_names=["x1"],
    rounded = True,
    filled = True
)

将dot文件转成png文件：dot -T png regression_tree.dot -o regreesion_tree.png

# 图片展示
from IPython.display import Image
Image(filename="regreesion_tree.png",width=600,height=600)

在进行回归任务时，可以选择参数来进行分裂，一般情况下都以均方误差，通过比较与均值的距离来进行树的分裂；

且为二叉树，所用模型为回归树（CART）。

• 回归任务中，树的深度对结果的影响

from sklearn.tree import DecisionTreeRegressor

# 构造两个树模型，其深度不同
tree_reg1 = DecisionTreeRegressor(random_state=42, max_depth=2)
tree_reg2 = DecisionTreeRegressor(random_state=42, max_depth=3)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)

# 预测值画图
def plot_regression_predictions(tree_reg, X, y, axes=[0, 1, -0.2, 1], ylabel="$y$"):
    x1 = np.linspace(axes[0], axes[1], 500).reshape(-1, 1)
    y_pred = tree_reg.predict(x1)
    plt.axis(axes)
    plt.xlabel("$x_1$", fontsize=18)
    if ylabel:
        plt.ylabel(ylabel, fontsize=18, rotation=0)
    plt.plot(X, y, "b.")
    plt.plot(x1, y_pred, "r.-", linewidth=2, label=r"$\hat{y}$")

plt.figure(figsize=(11, 4))
plt.subplot(121)

plot_regression_predictions(tree_reg1, X, y)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
    plt.plot([split, split], [-0.2, 1], style, linewidth=2)
plt.text(0.21, 0.65, "Depth=0", fontsize=15)
plt.text(0.01, 0.2, "Depth=1", fontsize=13)
plt.text(0.65, 0.8, "Depth=1", fontsize=13)
plt.legend(loc="upper center", fontsize=18)
plt.title("max_depth=2", fontsize=14)

plt.subplot(122)

plot_regression_predictions(tree_reg2, X, y, ylabel=None)
for split, style in ((0.1973, "k-"), (0.0917, "k--"), (0.7718, "k--")):
    plt.plot([split, split], [-0.2, 1], style, linewidth=2)
for split in (0.0458, 0.1298, 0.2873, 0.9040):
    plt.plot([split, split], [-0.2, 1], "k:", linewidth=1)
plt.text(0.3, 0.5, "Depth=2", fontsize=13)
plt.title("max_depth=3", fontsize=14)

plt.show()

树的深度越高，切分的越细。

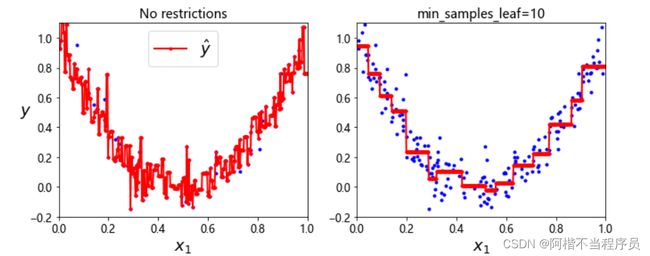
• 叶子结点最小样本个数的不同

# 叶子结点最小样本个数的不同
tree_reg1 = DecisionTreeRegressor(random_state=42)
tree_reg2 = DecisionTreeRegressor(random_state=42, min_samples_leaf=10)
tree_reg1.fit(X, y)
tree_reg2.fit(X, y)

x1 = np.linspace(0, 1, 500).reshape(-1, 1)
y_pred1 = tree_reg1.predict(x1)
y_pred2 = tree_reg2.predict(x1)

plt.figure(figsize=(11, 4))

plt.subplot(121)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred1, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", fontsize=18, rotation=0)
plt.legend(loc="upper center", fontsize=18)
plt.title("No restrictions", fontsize=14)

plt.subplot(122)
plt.plot(X, y, "b.")
plt.plot(x1, y_pred2, "r.-", linewidth=2, label=r"$\hat{y}$")
plt.axis([0, 1, -0.2, 1.1])
plt.xlabel("$x_1$", fontsize=18)
plt.title("min_samples_leaf={}".format(tree_reg2.min_samples_leaf), fontsize=14)

plt.show()

左图未限制时，会产生过拟合；而右图作出了限制后，有效的避免了这个问题。

这就是用决策树解决回归问题。