机器学习—深度神经网络

• 机器学习流程：数据获取、特征工程（难度）、建立模型、评估与应用

• 特征工程的作用

数据特征决定了模型的上限，预处理和特征提取是最核心的，算法与参数选择决定了如何逼近这个上限。

深度学习就是解决特征提取这个问题。

• 机器学习常规套路

  1. 收集数据并给定标签
  2. 训练一个分类器
  3. 测试，评估

• k近邻算法

流程：

1. 计算已知类别数据集的点与当前点的距离
2. 按照距离依次排序
3. 选取与当前点距离最小的k个点
4. 确定前k个点所在类别的出现概率
5. 返回前k个点出现频率最高的类别作为当前点预测分类

• 数据库样例：CIFAR-10

10类标签，5万个训练数据，1万个测试数据，大小均32*32。

• 距离选择

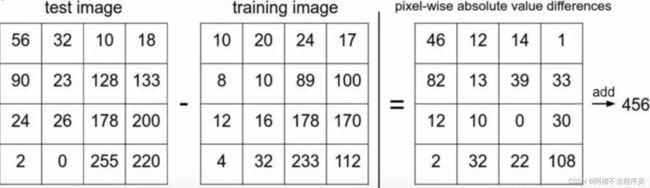
图像距离计算方式：

测试集与训练集对应像素点相减取，再取绝对值后求和，得到距离。

经过测试后，测试结果：部分结果还可以，但有些图没有分类成功。

其原因在于，k近邻算法把全局当做判断对象，而没有考虑主体（主要成分）在哪。

如此，神经网络最重要的部分就是区分主体。

计算方法

• 线性函数

从输入 --> 输出的映射：

其中，$x$对应像素点的值，$W$对应权重参数。

那么，它们分别构成$3072\ast 1$和$1\ast 3072$ 的矩阵表示，则两矩阵相乘的结果为一个值；

假如是10分类任务，那么要计算出各自的分类得分，则$Wx$的值就是$10\ast 3072$的矩阵；

其中，每列表示每个像素点所对应每个分类的权重参数，行代表类别的结果，$b$ 为偏置项微调结果。

若将图像划分成四个区域，做三分类任务：

$W$为 $3\ast 4$ 的矩阵表示权重参数，$x_i$ 为 $ 4*1 $ 表示四个区域的像素点值；

通过 $Wx+b$ 得到三个类别的总得分。

apparently，权重参数越大，表示对这一类别重要；正负亦如此。

最终的分类结果得分，是与权重参数有关，而与数据是无关的。

考虑权重参数得到的分类结果要用损失函数来衡量。

损失函数

• 假设损失函数为：

$$L_i=\sum _{j\ne y_i}max(0,s_j-s_{y_i}+1)$$

给出三个类别数据：

其中，$s_j$ 表示预测值，$s_{y_i}$表示真实值，$+1$相当于包容程度；

如第一列数据，将该数据错误预测成了car，则代入公式有：
$$\begin{gathered} max(0,5.1-3.2+1)+max(0,-1.7-3.2+1) \\ =2.9+0 \\ =2.9 \end{gathered}$$
表示当前损失为2.9。

亦如，第二列数据得到损失为0，则表示分类较好。

• 如果损失函数的值相同，意味着两个模型一样吗？

不一样。

• 损失函数 = 数据损失 + 正则化惩罚项

$$L=\frac{1}{N}\sum _{i=1}^N\sum _{j\ne y_i}max(0,f(x_i;W{)}_j-f(x_i;W)y_i+1)+\lambda R(W)$$

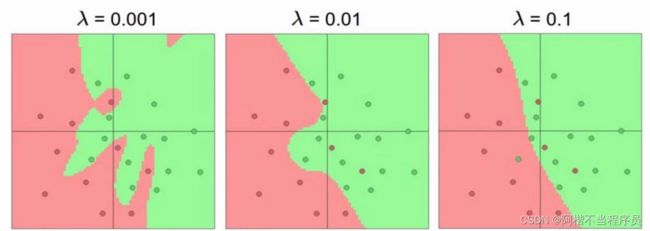
其中，$\lambda$ 为正则化惩罚项，因为神经网络太强了，需要避免过拟合；

λ越大，则惩罚力度越大；反之越小。

Softmax分类器

• 如何把一个得分转换成一个概率值？

$$g(z)=\frac{1}{1+e^{-z}}$$

先将得分映射到sigmod函数中。

• 归一化

$$P(Y=k|X=x_i)=\frac{e^s}{{\sum }_j{e}^{s}j}S=f(x_i;W)$$

• 计算损失值

$$L_i=-logP(Y=y_i|X=x_i)$$

再归一化可得概率，然后再通过log函数的性质，求出损失值。

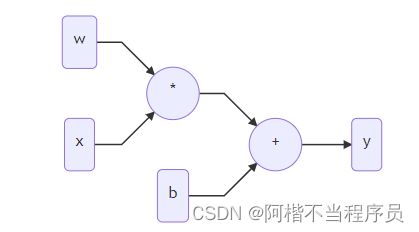
前向传播和反向传播

• 前向传播

上述操作步骤叫做前向传播，即输入x与w ——> 输出损失

• 反向传播
  • 利用梯度下降，多次计算后，找到最小的损失值
    

通过得到的损失值，对其进行链式求导，逐层进行计算。

由A到传播B，即由$ ∂L/∂A $得到$ ∂L/∂B $，由导数链式法则$ ∂L/∂B=(∂L/∂A)⋅(∂A/∂B)$ 实现。所以神经网络的BP就是通过链式法则求出 L 对所有参数梯度的过程。

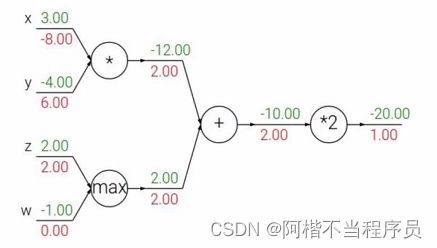
• 复杂的例子

$$f(w,x)=\frac{1}{1+e^{-(w_{0}x0+w_1{x}_1+w_2)}}$$

• 加法门单元：如$x+y=q$求导之后，均等分配
• MAX门单元：只把梯度给最大的
• 乘法门单元：如$x\ast y=q$求导之后，互换的感觉

神经网络整体架构

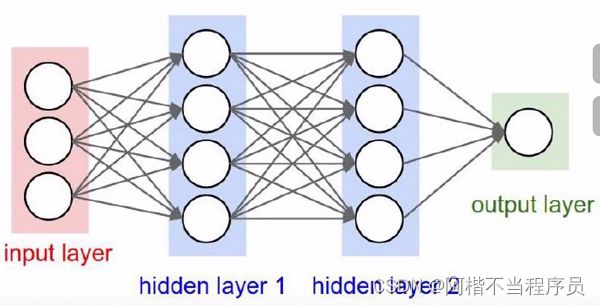
• 层次结构：

  输入层 —— 隐藏层 —— 输出层

  神经网络具有层次结构，每一层都是对前一层所做出的结果再进行处理。

• 神经元

在输入层相当于输入的特征个数。

• 全连接

每个点与下一层的点都有连接；从输入层 $[1\ast 3]$ 到隐藏层1 $[1\ast 4]$ 是做了一个矩阵乘法 $[1\ast 3]\ast [3\ast 4]=[1\ast 4]$

（$[3\ast 4]$是构造出的数据矩阵大小）

取得隐藏层1的结果，输入到隐藏层2中 $[1\ast 4]\ast [4\ast 4]=[1\ast 4]$；

在隐藏层里通过反向传播计算出最好的组合方式。

• 非线性

通过非线性函数，在每一次构造完数据的矩阵后进行变换。

$$\begin{gathered} 基本结构：f=W_{2}max(0,W_{1}x) \\ 继续堆叠下一层：f=W_3(0,W_{2}max(0,W_{1}x)) \end{gathered}$$

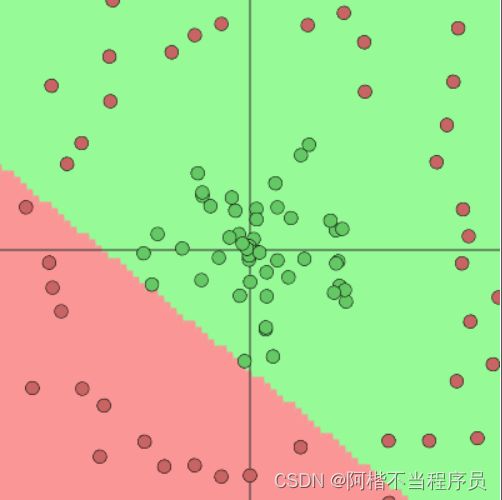
神经元个数对结果的影响

• 1个神经元

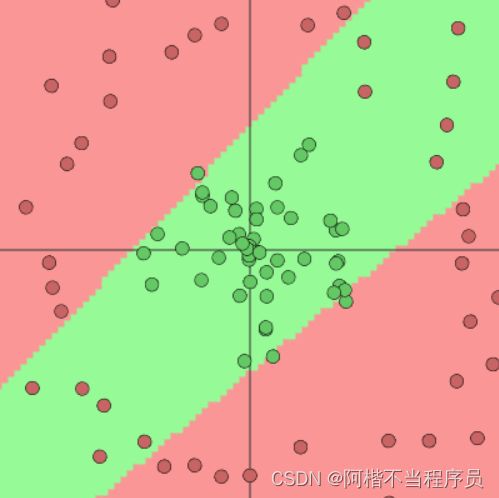
• 2个神经元

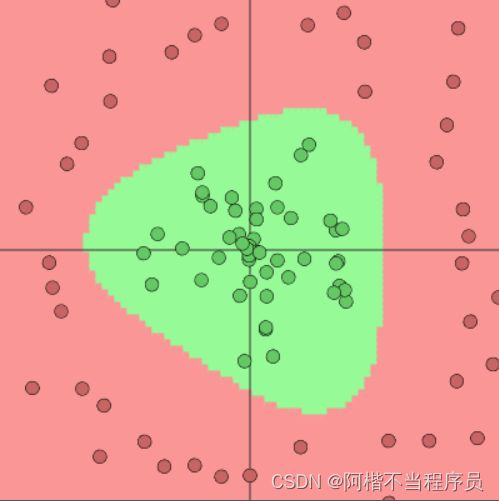
• 3个神经元

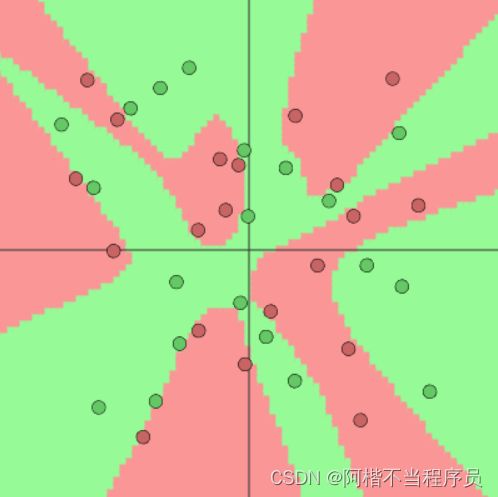
• 结论：神经元个数越多，决策效果越好，过拟合风险也越大

• 对于随机数据，神经网络也可以正确的找到规律：

正则化与激活函数

• 正则化的作用

惩罚力度对结果的影响：

惩罚越小，过拟合风险越大。

• 激活函数

神经网络中的每个神经元节点接收上一层神经元的输出值作为本神经元的输入值，并将输入值传递给下一层，输入层神经元节点会将输入属性值直接传递给下一层（隐藏层或输出层）；

在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系， 这个函数称为激活函数。

激活函数其实是指如何把“激活的神经元的特征”通过函数把特征保留并映射出来，即负责将神经元的输入映射到输出端。

常用的激活函数：Sigmoid,Relu,Tanh等。

• Sigmoid

  

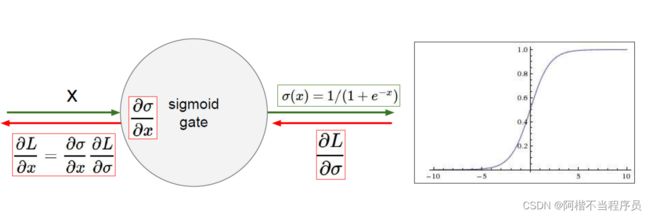
sigmod的软饱和性：

其两侧导数逐渐趋近于0，具体来说，由于后向传递过程中，sigmoid向下传导的梯度包含了一个 $f^{\prime }(x)f^{\prime }(x)$ 因子，因此一旦输入落入饱和区， $f^{\prime }(x)f^{\prime }(x)$ 就会变得接近于0，导致了向底层传递的梯度也变得非常小。

此时，出现的梯度消失现象，对后面的梯度就不进行更新了。

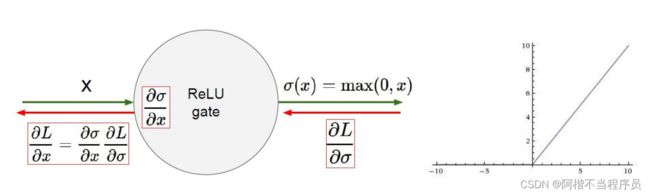
• Relu

优势：

• 没有饱和区，不存在梯度消失问题，防止梯度弥散；
• 稀疏性；
• 没有复杂的指数运算，计算简单、效率提高；
• 实际收敛速度较快，比Sigmoid/tanh快得多；
• 比Sigmoid更符合生物学神经激活机制。

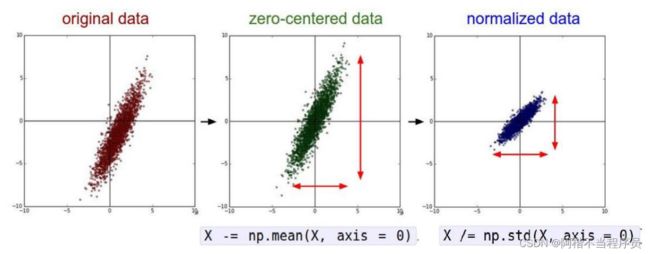
• 数据预处理

不同的预处理结果会使得模型的效果发生很大的差异。

zero-centered data：去中心化。

normalizedd data：标准化。

• 权重参数初始化

参数初始化同样非常重要。

W = 0.01 * np.random.randn(D,H)

D，H代表矩阵维度，乘上0.01是为了让初始化的值尽可能的小，且趋于稳定的状态；

通常都使用随机策略来进行初始化。

神经网络过拟合解决方法

• DROP-OUT（七伤拳）
  

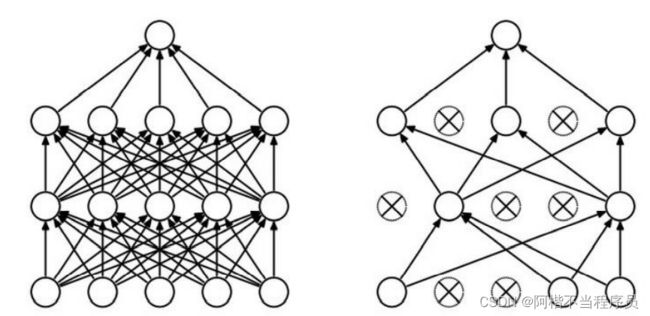
神经网络中，节点与节点之间都是全连接的一个状态（左图）；

训练需要很多次，若在每层每一次都随机选择部分的节点进行参与，使模型更加的简单，即DROP-OUT；

而在测试阶段，还是使用全连接的模型进行测试即可。