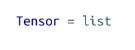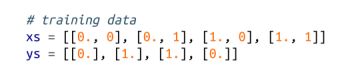从0开始，基于Python探究深度学习神经网络

来源 |  Data Science from Scratch， Second Edition

作者 | Joel Grus

全文共6778字，预计阅读时间50分钟。

深度学习

 

1.  张量

2.  层（Layer）的抽象

3.  线性层

4.  神经网络作为一个层的序列

5.  损失和优化

6.  示例：XOR 重新实现

7.  其他激活函数

8.  示例：重新实现 FizzBuzz

9.  softmax 和交叉熵（cross-entropy）

10.  Dropout

11.  例子：MNIST

12.  保存和加载模型

13.  以供进一步探索

深度学习最初指的是“深度”神经网络（即具有多个隐藏层的网络）的应用，尽管实际中这个术语现在包含各种各样的神经结构。

 

在本章中，我们将基于之前的工作，研究更广泛的神经网络。为此，我们将引入一些抽象概念，允许我们以更普遍的方式思考神经网络。

 

张量

以前，我们对向量（一维数组）和矩阵（二维数组）进行了区分。当我们开始使用更复杂的神经网络时，我们也需要使用高维数组。

 

在许多神经网络库中，n维数组被称为张量，我们也会这样叫。(不把n维数组称为张量是有迂腐的数学原因的；如果你是这样一个书呆子，你的反对意见会被注意到。)

 

如果我写一本关于深度学习的书，我会实现一个功能齐全的张量类，它重载Python的算术运算符，并可以处理各种其他操作。这样的实施本身就需要一整个章节。在这里我们会取巧，说一个张量只是一个list。这在一个方向上是正确的——我们所有的向量、矩阵和高维类似物都是列表。在另一个方向当然不是真的——大多数Python列表在我们看来不是n维数组。

 

注意

理想情况下，你可能这样认为：

但是，Python不允许你定义这样的递归类型。即使它这样做了，这个定义仍然不正确，因为它允许坏的“张量”，比如：[[1.0,2.0]，[3.0]]，它们的行大小不同，这使得它不是一个n维数组。

所以，就像我说的，我们只会取巧，认为：

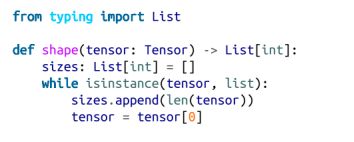
我们将编写一个辅助函数来找到一个张量的大小：

 

 

因为张量可以有任意数量的维度，所以我们通常需要递归地处理它们。我们将在一维情况下做一件事，并在高维情况下进行递归：

 

我们可以用它来编写一个递归的tensor_sum函数：

 

如果你不习惯递归思考，你应该思考直到弄明白它的意思，因为我们将在本章使用相同的逻辑。但是，我们将创建一些辅助函数，以便我们不必在各处重写此逻辑。第一个方法将一个函数单独应用于单个张量：

 

我们可以使用它来编写一个函数，它创建一个与给定张量形状相同的零张量：

 

我们还需要对两个张量的相应元素应用函数（最好是完全相同的形状，尽管我们不会检查）：

 

 

层（Layer）的抽象

 

在前一章中，我们建立了一个简单的神经网络，允许我们堆叠两层神经元，每层神经元都计算sigmoid（dot（weights, inputs））。

 

虽然这可能是实际神经元的理想化表示，但实际实践中我们希望允许更广泛的事情。也许我们希望神经元能记住他们以前的输入。也许我们想使用不同于sigmoid的激活函数。而且我们经常希望使用两层以上的隐含层。(我们的feed_forward函数实际上处理了任意数量的层，但我们的梯度计算没有。)

 

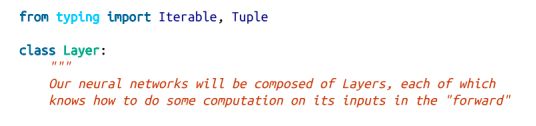
在本章中，我们将构建实现各种神经网络的机制。我们的基本抽象将是Layer，它知道如何将一些函数应用到其输入中，并知道如何反向传播梯度。

 

思考我们在第18章中构建的神经网络的一种方式是作为一个“线性”层，然后是一个“sigmoid”层，然后是另一个线性层和另一个“sigmoid”层。我们没有用这些术语来区分它们，但这样做将允许我们尝试使用更一般的结构：

 

 

正向和反向的方法将必须在我们的具体子类中实现。一旦我们建立了一个神经网络，我们就需要使用梯度下降来训练它，这意味着我们就需要使用其梯度来更新网络中的每个参数。因此，我们坚持认为每一层都应该能够告诉我们它的参数和梯度。

 

某些层（例如，对其每个输入应用sigmoid函数的层）没有需要更新的参数，因此我们提供了处理这种情况的默认实现。让我们来看看这一层：

 

这里有几件事需要注意到。一种是在向前传递过程中，我们保存了计算出的sigmoid，这样我们就可以在反向传递中使用它们。我们的Layer通常需要做这种事情。

 

其次，你可能会想知道sig*（1-sig）* grad来自哪里。这是微积分中的链规则，对应于我们之前的神经网络中的output（1-output）（output - target）项。

 

最后，你可以看到我们是如何使用tensor_apply和tensor_combine函数的。我们的大多数层都将类似地使用这些函数。

 

 

线性层

 

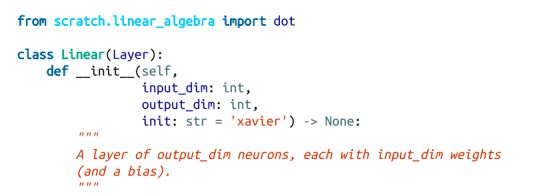
我们需要复制第18章的神经网络是“线性”层，代表神经元的dot（weight，input）部分。

 

该层将有参数，我们希望用随机值初始化这些参数。

 

结果证明，初始参数值可以对网络运行的速度（有时是是否能够运行）产生巨大的影响。如果权重太大，它们可能在激活函数具有接近零梯度的范围内产生大输出。而网络中梯度为零的部分必然不能通过梯度下降学习任何东西。

 

因此，我们将实现三种不同的方案来随机生成权值张量。首先是从[0,1]上的随机均匀分布（即random.random()）中选择每个值。第二种值（这种策略是默认策略）是从标准正态分布中随机选择每个值。第三种是使用Xavier初始化，其中每个权重由均值为0，方差为2/(num_inputs+num_outputs)的正态分布随机抽取。事实证明，这通常对神经网络权值很有效。我们将使用random_uniform函数和random_normal函数来实现这些功能：

 

 

然后将它们全部包装在一个random_tensor函数中：

 

现在我们可以定义我们的线性层了。我们需要用输入的维度（它告诉我们每个神经元需要多少权重)、输出的维度(它告诉我们应该有多少神经元）和我们想要的初始化方案来初始化它：

 

注意

本章中的一些网络我根本无法使用不同的初始化方法进行训练，现在我相信你知道初始化方案有多重要了。

forward方法易于实现。我们将得到每个神经元的一个输出，并一直放在一个向量中。每个神经元的输出是其输入与权重的内积（dot），加上其偏差：

 

backward方法更复杂，但如果你知道微积分并不难：

 

 

注意

在“真正的”张量库中，这些（以及许多其他）操作将表示为矩阵或张量乘法，这些库设计得非常快。我们的库速度很慢。

最后，在这里，我们确实需要实现params和grads。我们有两个参数和两个相应的梯度：

 

 

神经网络作为一个层的序列

 

我们希望将神经网络视为层的序列，所以让我们想出一种将多层组合到一起的方法。所得到的神经网络本身是一个层，它以下面明显的方式实现了该层的方法：

 

 

所以我们可以将我们用于XOR的神经网络表示为：

 

但我们仍然需要更多的机器来训练它。

 

损失和优化

 

之前，我们为我们的模型编写了单个损失函数和梯度函数。这里我们希望试验不同的损失函数，因此（如往常）我们将引入一个新的损失抽象，它封装损失计算和梯度计算：

 

我们已经处理了很多次损失，这个损失就是平方误差的总和，所以我们应该很容易地实现它。唯一的诀窍是，我们需要使用tensor_combine：

 

 

（后面我们将查看不同的损失函数。）

 

最后一件要处理的事情是梯度下降。在整本书中，我们通过一个训练循环手动完成了所有的梯度下降：

在这里，这对我们不太有效，有几个原因。首先，我们的神经网络将有许多参数，我们需要更新所有参数。第二，我们希望能够使用更聪明的梯度下降变体，而且我们不想每次都要重写它们。

 

因此，我们将引入一个（你猜到了）优化器抽象，那么梯度下降就可以看成一个具体实例：

 

之后，再次使用tensor_combine轻松实现梯度下降：

 

 

唯一令人惊讶的是“切片分配”，这反映了重新分配列表不会改变其原始值的事实。也就是说，如果你只是计算了param=tensor_combine（……），你将重新定义局部变量param，但你不会影响存储在神经网络层中的原始参数张量。但是，如果你给slice[：]赋值，它实际上会更改列表中的值。

 

下面是一个简单的示例来演示：

 

如果你对Python缺乏经验，这种行为可能令人惊讶，所以思考一下，自己尝试例子，直到弄懂为止。

 

要演示此抽象定义的价值，让我们实现另一个使用动量（momentum）的优化器。其想法是，我们不想对每个新梯度反应过度，因此我们动态地保持我们看到的梯度的平均值，用每个新梯度进行更新，并朝着平均方向迈出一步：

 

因为我们使用了一个优化器抽象，所以我们可以很容易地在不同的优化器之间切换。

 

示例：XOR重新实现

 

让我们看看使用我们的新框架来训练能够计算XOR的网络是多么容易。我们首先要重新创建训练数据：

 

然后我们定义网络，尽管现在我们暂时不考虑最后一个sigmoid层：

 

我们现在可以编写一个简单的训练循环，现在我们还可以使用优化器和损失的抽象。这使我们可以轻松地尝试不同的方法：

 

这应该训练得很快，你应该看到损失会下降。现在我们可以检查一下权重了：

 

对于我的网络，我大致发现：

 

所以如果两个输入都不是1，hidden1激活。如果两个输入都是1，hidden2激活。如果两个隐藏输出都不是1，输出就会激活（也就是说，如果两个输入不相同则激活，两个输入不同则激活）。事实上，这正是XOR的逻辑。

 

请注意，这个网络学习到的特性与我们在第18章中训练到的特性不同，但它们任然试图做同样的事情。

 

 

其他激活函数

 

sigmoid函数失宠有几个原因。一个原因是sigmoid（0）等于1/2，这意味着一个输入和为0的神经元有一个正输出。另一个问题是，对于非常大和非常小的输入，它的梯度非常接近0，这意味着它的梯度会“饱和”，其权重更新可能会卡住。

 

一个流行的替代方法是tanh（“双曲切线”），它是一个不同的符号形函数，范围从-1到1，如果输入为0，则输出为0。tanh(x)的导数是1-tanh(x)**2，这使得该层易于构建：

 

 

在较大的网络中，另一种流行的替代方法是Relu，当输入为负时值为0，当输入为正时等价于恒等函数：

 

还有许多其他的函数。我鼓励你在你的网络中多尝试。

 

示例：重新实现FizzBuzz

 

我们现在可以使用“深度学习”框架从“FizzBuzz”重现我们的解决方案。让我们来设置这些数据：

 

并创建该网络：

 

在训练时，我们还要跟踪训练集的准确性：

 

 

经过1000次训练迭代，模型在测试集上的准确率达到90%；如果训练时间更长，它应该做得更好。（我不认为仅仅25个隐藏单元就能训练到100%准确，但如果你达到50个隐藏单元，则绝对有可能。）

 

softmax和交叉熵（cross-entropy）

 

我们在前一节中使用的神经网络以sigmoid层结束，这意味着它的输出是一个在0到1之间的数字向量。特别是，它可以输出一个完全为0s的向量，也可以输出一个完全为1s的向量。但是，当我们处理分类问题时，我们希望为正确的类输出1，为所有不正确的类输出0。一般来说，我们的预测不会那么完美，但我们至少希望预测类上的实际概率分布。

 

例如，如果我们有两个类，并且我们的模型输出[0,0]，很难理解。它认为输出不属于任何一个类吗？

 

但是如果我们的模型输出[0.4,0.6]，我们可以把它解释为预测我们的输入属于第一类的概率为0.4，我们输入属于第二类的概率为0.6。

 

为了实现这一点，我们通常放弃最后的sigmoid层，而使用softmax函数，它将一个实数向量转换为一个概率向量。我们计算向量中的每个数的exp(x)，从而得到一个正数的向量。在那之后，我们只把每个正数除以和，这就得到了累加值为1的向量，也就是一个概率向量。

 

如果我们最终尝试计算，比如，exp（1000），我们会得到一个Python错误，所以在取exp之前，我们减去最大的值（这样处理会获得相同的概率），这样就让在Python中的计算更安全：

 

一旦我们的网络产生概率，我们经常使用不同的损失函数称为交叉熵（有时“负对数似然”)。

 

你可能还记得，在“最大似然估计”中，我们通过验证（在某些假设下）最小二乘系数使观察数据的可能性最大化，来证明在线性回归中使用最小二乘是合理的。

 

在这里我们可以做类似的事情：如果我们的网络输出是概率，交叉熵损失表示观测数据的负对数可能性，这意味着最小化损失与最大化训练数据的对数似然（因此似然）是一样的。

 

通常，我们不会将softmax函数作为神经网络本身的一部分。这是因为，如果softmax是损失函数的一部分，而不是网络本身的一部分，那么关于网络输出的损失梯度就很容易计算出来。

 

 

如果我现在使用SoftmaxCrossEntropy损失来训练相同的FizzBuzz网络，我发现它通常训练得更快（也就是说，花更少的epochs）。这大概是因为找到Softmax给定分布的权重比找到sigmoid给定分布的权重要容易得多。

 

也就是说，如果我需要预测类0（第一个位置为1，其余位置为0的向量），在 linear + sigmoid 情况下，我需要第一个输出是大正数，其余输出是大负数。然而，在softmax的情况下，我只需要第一个输出大于剩余的输出。显然，第二种情况有更多的可能，这表明应该更容易找到这样的权重：

 

 Dropout

像大多数机器学习模型一样，神经网络很容易过度拟合它们的训练数据。我们之前已经看到过改善这一点的方法；例如，在“正则化”中，我们惩罚了大的权重，这有助于防止过度拟合。

 

正则化神经网络的一种常见方法是使用dropout。在训练时，我们用一些固定的概率随机关闭每个神经元（即将其输出替换为0）。这意味着网络不能学习依赖于任何单个神经元，这似乎有助于解决过度拟合问题。

 

在评估时，我们不想dropout任何神经元，所以dropout层需要知道它是否在训练。此外，在训练时，dropout层只传递其输入的一些随机部分。为了使其输出在评估期间可比较，我们将使用相同比例（均匀）缩小输出：

 

 

我们将使用此方法来帮助我们防止深度学习模型过度拟合。

 

 

例子：MNIST

 

MNIST是一个每个人都用来学习深度学习的手写数字数据集。

 

它有一种有点棘手的二进制格式，因此我们将安装mnist库来使用它。（是的，从技术上讲，这部分并不是“从零开始”。）

然后我们可以加载数据：

 

让我们绘制前100张训练图像，了解它们的形状（图19-1）：

 

MNIST图像

你可以看到，它们看起来确实像手写的数字。

注意

我第一次尝试显示这些图像，结果是黑色背景上的黄色数字。我既不聪明也不微妙，不知道我需要添加cmap=Greys来获得黑白图像；我通过谷歌搜索，找到了堆栈溢出的解决方案。作为一名数据科学家，你将非常熟练于这个工作流程。

我们还需要加载测试图像：

 

 

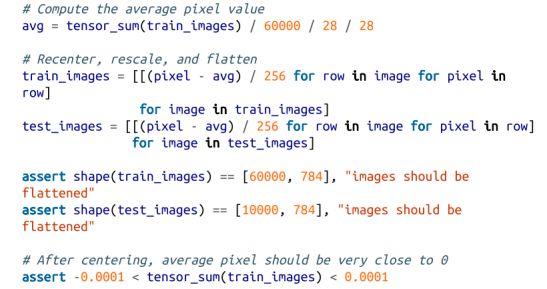
每张图像为28×28像素，但我们的线性层只能处理一维输入，因此我们将使它们变平（并除以256以使它们在0和1之间）。此外，如果我们的输入平均为0，神经网络训练更好，因此我们将减去平均值：

 

我们还想要对目标进行一次热编码，因为我们有10个输出。首先，让我们编写一个one_hot_encode函数：

 

然后将其应用于我们的数据中：

 

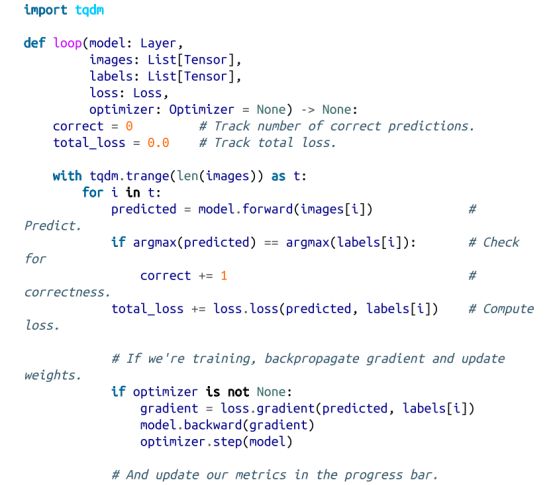
我们抽象的优点之一是，我们可以对各种模型使用相同的训练/评估循环。所以，让我们先写下这个问题吧。我们将传递我们的模型、数据、损失函数以及（如果我们正在训练）优化器。它将传递我们的数据、跟踪性能以及（如果我们传递了优化器）更新我们的参数：

 

              

作为一个基线，我们可以使用我们的深度学习库来训练一个（多类）逻辑回归模型，它只是一个线性层，然后是一个softmax。这个模型（本质上）只寻找10个线性函数，这样如果输入代表，比如说，一个5，那么第5个线性函数就会产生最大的输出。

 

通过我们的6万个训练实例就足以学习这个模型了：

 

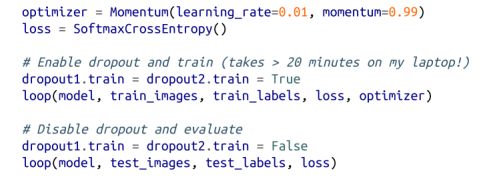
这种准确率约为89%。让我们看看使用深度神经网络能否做得更好。我们将使用两个隐藏层，第一层有30个神经元，第二层有10个神经元。我们将使用Tanh激活函数：

 

 

我们也可以使用相同的训练循环！

 

我们的深度模型在测试集上的精度优于92%，这与简单的logistic模型相比是一个很好的改进。

 

注意

MNIST网站（http://yann.lecun.com/exdb/mnist/）描述了各种性能优于这些模型的模型。其中许多都可以使用我们迄今为止开发的方法来实现，但这需要非常长的时间才能在张量列表框架（lists-as-tensors）中进行训练。一些最好的模型涉及到卷积层，这很重要，但不幸的是，这完全超出了一本关于数据科学的介绍性书的范围。

 

保存和加载模型

这些模型需要很长时间来训练，所以如果我们能保存它们，这样就不用每次训练它们就好了。幸运的是，我们可以使用json模块轻松地将模型权重序列化到文件中。

 

为了保存，我们可以使用Layer.params来收集权重，将它们粘贴在一个列表中，并使用json.dump将该列表保存到一个文件中：

 

把权重加载回去只是需要多做一点工作。我们只使用json.load从文件中获取权重列表，并通过切片（slice）分配来设置模型的权重。

 

(特别是，这意味着我们必须自己实例化模型，然后加载权重。另一种方法也是保存模型体系结构的一些表示，并使用它来实例化模型。这不是一个可怕的想法，但它需要更多的代码和更改我们的所有层，所以我们将坚持更简单的方法。）

 

在加载权重之前，我们要检查它们的形状是否与我们要加载到的模型参数相同。（这是一种保障，例如尝试将保存深度网络的权重加载到浅网络或类似问题。）

 

注意

JSON将数据存储为文本，这使得它成为一种非常低效的表示。在实际应用程序中，你可能会使用pickle序列化库，它将内容序列化为更高效的二进制格式。在这里，我决定保持它的简单性和可读性。

 

你可以从书中的GitHub存储库(https://github.com/joelgrus/data-science-from-scratch)中下载我们训练的各种网络的权重。

 

以供进一步探索

深度学习现在真的很热，在这一章中，我们几乎只涉及到皮毛。关于你想知道的深度学习的任何方面，都有很多的好书籍和博客文章（当然，也有许多很糟糕的博客文章）。

 

· 由伊恩·古德费罗、约舒亚·本吉亚和亚伦·考维尔（麻省理工学院出版社）撰写的标准教科书《深度学习》可以在网上免费提供（https://www.deeplearningbook.org/）。它很好，但它涉及到相当多的数学知识。

· 弗朗索瓦·乔莱特的Python深度学习（Manning）是一个伟大的介绍Keras库，之后我们的深度学习库有点模式化了（基本都吸收了Keras的风格）。

· 我自己主要使用PyTorch来进行深度学习。它的网站上有很多文档和教程。

更多精彩推荐
Windows 11 上手机！小米 8、一加 6T、微软 Lumia 950 XL 都可以运行

深度学习教你重建赵丽颖的三维人脸

Openpose+Tensorflow 这样实现人体姿态估计 | 代码干货

点分享点收藏点点赞点在看