大数据时代，你应该知道的生活真相（下）

本文写于2016年，由于未标注原创，因此这里再发一次，写得比较稚嫩，但一开始就是这样的

正文开始

接着上期，继续聊生活的真相，这次我们要谈谈药品检验造假、篮球中的手热效应、人人都是大胖子、单身汉约会法则、为什么高富帅总是很冷漠等有趣的话题，里面都蕴含着统计检验、线性思维、思维漏洞中的奇妙法则哦。

Part 1

颠覆统计检验

显著性检验原理

很多科学问题都可以简化为二选一的简单形式：某件事情正在发生，是还是不是？针对某种疾病研发的新药对改疾病确有疗效，还是作用为零？这种“作用是零”的情况叫作“零假设”。所谓零假设，指的是假设所研究的介入活动不起任何作用。那么，如何推翻零假设？我们可以借助某个标准框架-“显著性检验”。下面举个例子你就明白了：

我们需要做一个实验，找到100个实验对象，从中随机选取50人，让他们服用我们研发的新药，剩下的50人则服用安慰剂。我们显然希望服药病人的死亡率低于服用安慰剂的病人。

但是，如果我们观察到服药病人的死亡率低于服用安慰剂的病人，我们也不能说药物有效，仅仅证明数据和理论一致还不够，还要证明数据与反理论不一致，也就是排除讨厌的零假设。

这里的零假设就是：假设药物没有效果（即零假设为真），在观察结果中是否会出现极端情况，比如极小概率事件的发生，如果这个事件发生的概率小于0.05（一般叫P值），则说明实验结果具有统计显著性，我们需要推翻零假设；如果P值很大，则只能承认零假设没有被推翻。

以上例为例，假定零假设成立，这就意味着服用新药的50名病人与服用安慰剂的50名病人死亡率差不多（比如都是10%左右），即没有效果，假设在测试过程中，服用安慰剂的有5人死亡，而服用新药的病人无人死亡。则我们可以看看这种情况出现的概率，按照零假设，所有50个服用新药的病人全部存活的概率非常小，只有0.9*0.9*0.9…0.9=0.00515,即1/200,可能性这儿小（小于P=0.05），因此可以推翻零假设,则说明药物有效。

显著性检验体现了我们对不确定性的直觉推理，因此人们普遍接受这个方法。但是，真得是这样吗？

精神分裂的基因药靠谱吗？

中药的效用就不说了，其甚至一直没有勇气去进行显著性检验测试，但当报纸上刊登了某种药物通过了显著性检验，你以为就对了，那我们可能还是太天真了，在临床医学基于显著性检验不断发明新药的同时，“造假”也随之而来。

现代研究表明，基因对于精神分裂症是有影响的，由于这种疾病有遗传的可能，人们几乎可以肯定是基因在起作用，但是，起作用的基因位于基因序列的什么位置呢？研究人员可能会普遍撒网，对10万种基因进行检验，以期找出与精神分裂有关的基因，实际上，可能只有大约10种会对精神分裂产生影响。

但是，其余的99990种基因呢？这些基因与精神分裂没有任何关系，但是，其中的1/20或者说5000种基因，会顺利通过统计学显著性检验，哈哈，只要次数足够多，偶然性就会成为必然性，但是，当研究者将自己的论文发布出来的时候，除了介绍那次成功的基因实验，谁会说那余下的94990次实验呢。

上帝真得可以证明存在吗？

很多人尝试用显著性检验来证明上帝存在，首次尝试用数学语言做这个论断的人是阿布斯诺特，他研究1629-1710年的伦敦人口出生记录，发现了显著的规律性，在这81年间，每年出生的男孩都多于女孩，于是，他提出了一个疑问：在上帝不存在、新生儿性别随机分布这个零假设前提下，出现这个巧合情况的概率是多少呢？假设在任一年份，伦敦新生人口男孩多于女孩的概率为1/2，那么连续81年出现这种情况的概率几乎等于0，阿布斯诺特根据这个发现撰写了一篇论文，论文的题目为“神圣天意的论据-从新生儿性别研究中发现的永恒规律”。阿布斯诺特提出的这个论据受到了神学研究名流的普遍赞誉。

事实是这样吗，其它数学家迅速指出他的推理过程存在缺陷，主要是零假设不合理，即婴儿性别是随机确定的，生男孩女孩的概率相同吗？如果我们将一枚硬币抛82次，结果全部为正面，那么我们应该认为“硬币有问题”，而不是“上帝青睐硬币的正面”。

Part 2

相关性悖论

吸烟是肺癌的结果吗？

吸烟致癌现在基本已经盖棺定论了，因为两者有强烈的相关性，但相关性有可能是某些尚未被人们发现的共同原因造成的，因此令人困惑，但是更加难以捉摸的是，相关性还有可能是某些共同结果造成的。这个现象叫作“柏克森悖论”，其强烈怀疑吸烟与肺癌之间存在联系的观点，疑点是这样的：

人们发现吸烟不仅与肺癌存在相关性，而且会影响人体的所有系统，与多种疾病之间都有相关性，这个事实有点难以理解，因为烟草的危害过于全面和彻底，“如果人们已经确认某种药物可以缓解普通感冒，而调查发现这种药物不仅可以治疗伤风，还可以治愈肺炎、癌症等多种疾病，科学家就会认为“研究方法肯定出了问题”，与之相似，烟草业不可能危害人体的所有系统。

柏克森更倾向于“体质假设”，即吸烟者与非吸烟者之间预先存在的某种差异，是非吸烟者相对健康的原因。

如果85-95%的人口都是吸烟者，那些不吸烟的少数人就代表了某种特殊体质类型，我们不能确定这些人的平均寿命更长，但是这部分人的总体死亡率将相对低一些。烟草商无时不刻在劝诱我们吸烟，刺激我们的神经，但是，这一小部分人成功抵制住了诱惑，说明他们的意志力更强，既然他们可以抵制烟草商的诱惑，那么他们抵御肺癌的能力也应该更强。

不管你信不信，笔者也有点动摇了，真得是这样吗？我们一直以为的确凿事实真的值得怀疑吗？

高富帅真得很冷漠吗？

年轻女性可能注意到一个问题，在与你们约会的男性对象中，相貌英俊的往往不友善，而友善的又往往其貌不扬，难道因为男性五官端正而让女性觉得讨厌？还是因为友善导致男性相貌丑陋？来，用数学来帮你解释。

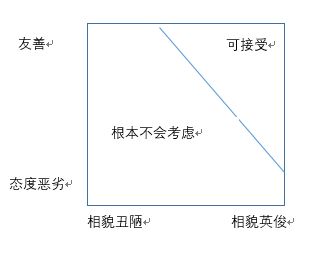
假设男性分布于整个正方形中，供分成4种类型：友善且英俊的男性，友善但相貌丑陋的男性，态度恶劣但英俊的男性，态度恶劣且相貌丑陋的男性，而且各种类型的男性人数大致相等。

友善与英俊有一个相同作用，即都会让女性注意到且具有该特点的男性。坦率地讲，女性根本不会考虑与那些太多恶劣且相貌丑陋的男性约会，因此，在下面这个大正方形中含有一个“可接受的男性特征小三角形”。

现在，我们可以找到上述现象出现的原因了。三角形中的那些英俊男性具有从友善到态度恶劣的不同特征，越是英俊的男生，态度恶劣的可能性就越大，其相貌与性格之间必然存在负相关关系，如果女性刻意让男性采取恶劣的态度以实现美化其相貌的目的，女性就会成为“柏克森悖论”的牺牲品。

Part 3

不要线性思维

人人都是大胖子

美国国家健康和营养调查选择大量具有代表性的美国人作为样本，跟踪调查他们的健康数据，内容涉及听力衰退、性传播疾病等多个方面。该研究还给出了超重美国人的精确占比，毫无疑问，在最近几十年内，美国人的超重现象越来越普遍，20世纪70年代初，体重指数超过25的美国人不足半数，到90年代初，这个数字接近60%，到2008年，几乎有3/4的美国人都超重了，据此我们可以进行线性回归，其分析的结果大致为：到2048年，这条线会超过100%

触目惊心数字游戏

中东矛盾有多严重？乔治敦大学反恐专家在《外交》杂志山给出了一些冰冷的数字：“以色列军方报告，从2000年至2005年10月底，有1074个以色列人死亡，7520人受伤，对以色列这样一个小国而言，这两个数字已经大得惊人，按照比例换算的话，相当于5万美国人死亡，30万美国人受伤”。摩尔不甘示弱，在《洛杉矶时报》上撰文指出：“在铸铅行动中，以色列人打死了1400个巴勒斯坦人，按比例换算，相当于杀死了30万个美国人，但是新任总统奥巴马对此保持沉默。

这是赤露露的“线性中心主义”，如果我们根据死亡人数在全国人口中所占比例来评判事件，那么在分析人口非常小的国家所发生的暴行时往往犯严重的错误，比如评判20世纪的暴行，排在前三位的是德国殖民者对纳米比亚赫雷罗人的大屠杀，波尔布特对柬埔寨人的屠杀和利奥波德国王在刚果发起的殖民战争，而希特勒的暴行却榜上无名。数学领域规避错误的一个重要原则是：实地测试某个数学方法时，可采用不同的方式进行计算，如果得到不同的结果，则说明我们使用的方法有问题。

Part 4

其它

单身汉如何成为女性心仪的约会对象

多头绒泡菌是一种非常有趣的微生物，其没有大脑，与所有生物一样，多头绒泡菌会做决策，当然，它作出的决策无非是“靠近我喜欢的东西（燕麦）”与“远离我不喜欢的东西（明亮的阳光）”，出于某种原因，多头绒泡菌在完成这类决策活动时效率极高。生物学家希望了解其决策机制。

在培养皿一侧放置3克燕麦（黑暗），在另一侧放置5克燕麦（明亮）并用紫外线照射燕麦，然后在中间放上多头绒泡菌，多头绒泡菌会怎么做？

他们发现，在这种情况下，多头绒泡菌选择两个方面的次数各占一半，更多的食物基本抵消了紫外线带来的不舒服，对于多头绒泡菌而言，黑暗中的一堆燕麦与明亮处的一大堆燕麦效用一样。因此，它会左右为难。如果把5克燕麦换成10克，则多头绒泡菌根本不在乎光线，每次都会朝10可燕麦靠近。从这个实验看，多头绒泡菌似乎相当理性。

但是，如果增加一种选择，比如在黑暗处再放置1克燕麦（黑暗），那么会怎样？令人惊奇的是，多头绒泡菌的喜好发生了变化，选择3克的燕麦（黑暗）是5克燕麦（明亮）的3倍。

有个波达计算方法为其做了解释，实现了某种形式的“民主”，比如，我们可以假设多头绒泡菌中的50%关心食物，而其余的50%优先考虑光强度，假设排名第一的得2分，第二的得1分，最后一名得0分。

5克燕麦（明亮），3克燕麦（黑暗），1克燕麦（黑暗）	50%
3克燕麦（黑暗）与1克燕麦（黑暗）并列，5克燕麦（明亮）	50%

因此，5克燕麦（明亮）从关心食物的半数多头绒泡菌那里得到2分，从优先考虑阳光的半数多头绒泡菌得到0分，因此总分为2*0.5+0*0.5=1，在并列第一时，我们给每个打1.5分，因此3克燕麦（黑暗）获得1.25分，1克燕麦（黑暗）得0.75分，根据得分，3克燕麦（黑暗）排在第一位，5克燕麦（明亮）排在第二位，而1克燕麦（黑暗）则排在最末，与实验结果一致。

本来，多头绒泡菌对光线较暗的小堆燕麦与光线较亮的大堆燕麦的喜爱程度相当，但是，如果再加入更小的堆的光线较暗的燕麦供选择时，经过比较，光线较暗的小堆燕麦似乎更加诱人，以致于多头绒泡菌几乎每次都放弃光线较亮的大堆燕麦。

这种现象叫“非对称性支配效应”，其他生物也会受到该效应的影响。生物学家发现，人也是如此，所以，如果你是一位正在寻找真爱的单身汉，那么，在考虑与哪位朋友一起去赴心仪对象的约会时，应该选择条件与你相似但略微逊色于你的那位，千万不要反过来哦。

在这个大数据时代，我们的身边充满了数据，这为数学的应用提供了无尽的想象，掌握了它，运用数学的逻辑，我们就可以透过现实世界错综复杂的表面现象，看清本质，从而更深入、跟准确地理解我们这个世界。

数据中的商机

大数据的过去、现在和未来：万字长文解读《大数据四十二条》

从吴军的“算法的油水就那么多”说起！

《长安十二时辰》的大案牍术可不是什么“穿越版”的大数据！

大数据在5G时代会有什么不同？

从计划到市场，精准营销也许到了该改变的时候了！

有了大数据这个工具，“社会科学”也许可以变得更让人信服！

如何进一步理解精准营销的内涵？

我如何用统计学指导自己的生活？

谈谈大数据时代的《别被算法困在“信息茧房”》

从大数据变现出发，如何清晰的理解新零售？

从吴恩达的“AI的壁垒非算法而是数据”说起！

大数据，悟道2016

宝洁，没必要去亵渎精准营销！

业务人员的革命：从大数据运营是一台“戏”开始

传统企业的模型最佳实践为什么很难复制推广？

一个大数据应用是如何炼成的？

不忘初心，大数据不是IT的狂欢！

传统企业大数据对内运营变现如何破局？

决战大数据的对内运营

谈谈我的《深入浅出大数据系列讲义课程》

重装上阵-大数据管理的实践和思考

“9·11”15年：致癌人数已超5400人，这个新闻靠谱吗？

天龙八步：传统企业大数据运营的一些思考

普及、开放与平台：大数据价值运营之路（上）

普及、开放与平台：大数据价值运营之路（中）

普及、开放与平台：大数据价值运营之路（下）

大数据时代，你应该知道的生活真相（上）

数据说谎的艺术

从“男人比女人孝顺”和“百度医疗竞价”说起，大数据需要科学和正直的品格

七剑下天山，谈谈我认识的精准营销