Sklearn官方文档中文整理6——交叉分解,朴素贝叶斯和决策树篇
Sklearn官方文档中文整理6——交叉分解,朴素贝叶斯和决策树篇
- 1. 监督学习
-
- 1.8. 交叉分解【cross_decomposition.PLSRegression,cross_decomposition.PLSCanonical,cross_decomposition.CCA,cross_decomposition.PLSSVD】
- 1.9. 朴素贝叶斯
-
- 1.9.1. 高斯朴素贝叶斯【naive_bayes.GaussianNB】
- 1.9.2. 多项分布朴素贝叶斯【naive_bayes.MultinomialNB】
- 1.9.3. 补充朴素贝叶斯【naive_bayes.ComplementNB】
- 1.9.4. 伯努利朴素贝叶斯【naive_bayes.BernoulliNB】
- 1.9.5. 基于外存的朴素贝叶斯模型拟合
- 1.10. 决策树
-
- 1.10.1. 分类【tree.DecisionTreeClassifier】
- 1.10.2. 回归【tree.DecisionTreeRegressor】
- 1.10.3. 多值输出问题
- 1.10.4. 复杂度分析
- 1.10.5. 实际使用技巧
- 1.10.6. 决策树算法: ID3, C4.5, C5.0 和 CART
- 1.10.7. 数学表达
-
- 1.10.7.1. 分类标准
- 1.10.7.2. 回归标准
1. 监督学习
1.8. 交叉分解【cross_decomposition.PLSRegression,cross_decomposition.PLSCanonical,cross_decomposition.CCA,cross_decomposition.PLSSVD】
交叉分解模块主要包含两个算法族: 偏最小二乘法(PLS)和典型相关分析(CCA)。
这些算法族具有发现两个多元数据集之间的线性关系的用途: fit method (拟合方法)的参数 X 和 Y 都是 2 维数组。

交叉分解算法能够找到两个矩阵 (X 和 Y) 的基础关系。它们是对在两个空间的协方差结构进行建模的隐变量方法。它们将尝试在X空间中找到多维方向,该方向能够解释Y空间中最大多维方差方向。 PLS回归特别适用于当预测变量矩阵具有比观测值更多的变量以及当X值存在多重共线性时。相比之下,在这些情况下,标准回归将失败。
包含在此模块中的类有:PLSRegression, PLSCanonical, CCA,PLSSVD
sklearn.cross_decomposition.PLSRegression
| 参数 | 解释 |
|---|---|
| n_components:int, default=2 | 要保留的组件数 |
| scale:bool, default=True | 是否缩放X和Y。 |
| algorithm:{‘nipals’, ‘svd’}, default=’nipals’ | 估计互协方差矩阵第一奇异向量的算法。“nipals”使用幂法,而“svd”将计算整个svd。 |
| max_iter:int, default=500 | algorithm='nipals’时幂法的最大迭代次数。否则忽略。 |
| tol:real, default 1e-06 | 幂法中用作收敛准则的容差:只要u i-u{i-1}的平方范数小于tol,算法就停止,其中u对应于左奇异向量。 |
| copy:bool, default=True | 是否在缩放前应用X和Y。如果为False,这些操作将就地执行,修改两个数组。 |
| 属性 | 解释 |
|---|---|
| x_weights_:ndarray of shape (n_features, n_components) | 每次迭代的互协方差矩阵的左奇异向量。 |
| y_weights_:ndarray of shape (n_targets, n_components) | 每个奇异交叉协方差矩阵的右交叉协方差。 |
| x_loadings_:ndarray of shape (n_features, n_components) | X的载荷。 |
| y_loadings_:ndarray of shape (n_targets, n_components) | Y的载荷。 |
| x_scores_:ndarray of shape (n_samples, n_components) | 变换后的训练样本。 |
| y_scores_:ndarray of shape (n_samples, n_components) | 转变后的训练目标。 |
| x_rotations_:ndarray of shape (n_features, n_components) | 用来变换X的投影矩阵。 |
| y_rotations_:ndarray of shape (n_features, n_components) | 用来变换Y的投影矩阵。 |
| coef_:ndarray of shape (n_features, n_targets) | 线性模型的系数,使得Y近似为Y=X@coef。 |
| n_iter_:list of shape (n_components,) | 每个组件的幂法迭代次数。如果算法=“svd”,则为空。 |
| 方法 | 解释 |
|---|---|
| fit(X, Y) | 拟合数据 |
| fit_transform(X[, y]) | 拟合数据并转换 |
| get_params([deep]) | 获取此估计器的参数。 |
| inverse_transform(X) | 转换回原始空间。 |
| predict(X[, copy]) | Predict targets of given samples. |
| score(X, y[, sample_weight]) | 返回预测的 R 2 R^2 R2确定系数。 |
| set_params(**params) | 设置此估计器的参数。 |
| transform(X[, Y, copy]) | 应用尺寸缩减。 |
例:
>>> from sklearn.cross_decomposition import PLSRegression
>>> X = [[0., 0., 1.], [1.,0.,0.], [2.,2.,2.], [2.,5.,4.]]
>>> Y = [[0.1, -0.2], [0.9, 1.1], [6.2, 5.9], [11.9, 12.3]]
>>> pls2 = PLSRegression(n_components=2)
>>> pls2.fit(X, Y)
PLSRegression()
>>> Y_pred = pls2.predict(X)
sklearn.cross_decomposition.PLSCanonical
| 参数 | 解释 |
|---|---|
| n_components:int, default=2 | 要保留的组件数 |
| scale:bool, default=True | 是否缩放X和Y。 |
| algorithm:{‘nipals’, ‘svd’}, default=’nipals’ | 估计互协方差矩阵第一奇异向量的算法。“nipals”使用幂法,而“svd”将计算整个svd。 |
| max_iter:int, default=500 | algorithm='nipals’时幂法的最大迭代次数。否则忽略。 |
| tol:real, default 1e-06 | 幂法中用作收敛准则的容差:只要u i-u{i-1}的平方范数小于tol,算法就停止,其中u对应于左奇异向量。 |
| copy:bool, default=True | 是否在缩放前应用X和Y。如果为False,这些操作将就地执行,修改两个数组。 |
| 属性 | 解释 |
|---|---|
| x_weights_:ndarray of shape (n_features, n_components) | 每次迭代的互协方差矩阵的左奇异向量。 |
| y_weights_:ndarray of shape (n_targets, n_components) | 每个奇异交叉协方差矩阵的右交叉协方差。 |
| x_loadings_:ndarray of shape (n_features, n_components) | X的载荷。 |
| y_loadings_:ndarray of shape (n_targets, n_components) | Y的载荷。 |
| x_scores_:ndarray of shape (n_samples, n_components) | 变换后的训练样本。 |
| y_scores_:ndarray of shape (n_samples, n_components) | 转变后的训练目标。 |
| x_rotations_:ndarray of shape (n_features, n_components) | 用来变换X的投影矩阵。 |
| y_rotations_:ndarray of shape (n_features, n_components) | 用来变换Y的投影矩阵。 |
| coef_:ndarray of shape (n_features, n_targets) | 线性模型的系数,使得Y近似为Y=X@coef。 |
| n_iter_:list of shape (n_components,) | 每个组件的幂法迭代次数。如果算法=“svd”,则为空。 |
| 方法 | 解释 |
|---|---|
| fit(X, Y) | 拟合数据 |
| fit_transform(X[, y]) | 拟合数据并转换 |
| get_params([deep]) | 获取此估计器的参数。 |
| inverse_transform(X) | 转换回原始空间。 |
| predict(X[, copy]) | Predict targets of given samples. |
| score(X, y[, sample_weight]) | 返回预测的 R 2 R^2 R2确定系数。 |
| set_params(**params) | 设置此估计器的参数。 |
| transform(X[, Y, copy]) | 应用尺寸缩减。 |
例:
>>> from sklearn.cross_decomposition import PLSCanonical
>>> X = [[0., 0., 1.], [1.,0.,0.], [2.,2.,2.], [2.,5.,4.]]
>>> Y = [[0.1, -0.2], [0.9, 1.1], [6.2, 5.9], [11.9, 12.3]]
>>> plsca = PLSCanonical(n_components=2)
>>> plsca.fit(X, Y)
PLSCanonical()
>>> X_c, Y_c = plsca.transform(X, Y)
sklearn.cross_decomposition.CCA
| 参数 | 解释 |
|---|---|
| n_components:int, default=2 | 要保留的组件数 |
| scale:bool, default=True | 是否缩放X和Y。 |
| max_iter:int, default=500 | algorithm='nipals’时幂法的最大迭代次数。否则忽略。 |
| tol:real, default 1e-06 | 幂法中用作收敛准则的容差:只要u i-u{i-1}的平方范数小于tol,算法就停止,其中u对应于左奇异向量。 |
| copy:bool, default=True | 是否在缩放前应用X和Y。如果为False,这些操作将就地执行,修改两个数组。 |
| 属性 | 解释 |
|---|---|
| x_weights_:ndarray of shape (n_features, n_components) | 每次迭代的互协方差矩阵的左奇异向量。 |
| y_weights_:ndarray of shape (n_targets, n_components) | 每个奇异交叉协方差矩阵的右交叉协方差。 |
| x_loadings_:ndarray of shape (n_features, n_components) | X的载荷。 |
| y_loadings_:ndarray of shape (n_targets, n_components) | Y的载荷。 |
| x_scores_:ndarray of shape (n_samples, n_components) | 变换后的训练样本。 |
| y_scores_:ndarray of shape (n_samples, n_components) | 转变后的训练目标。 |
| x_rotations_:ndarray of shape (n_features, n_components) | 用来变换X的投影矩阵。 |
| y_rotations_:ndarray of shape (n_features, n_components) | 用来变换Y的投影矩阵。 |
| coef_:ndarray of shape (n_features, n_targets) | 线性模型的系数,使得Y近似为Y=X@coef。 |
| n_iter_:list of shape (n_components,) | 每个组件的幂法迭代次数。如果算法=“svd”,则为空。 |
| 方法 | 解释 |
|---|---|
| fit(X, Y) | 拟合数据 |
| fit_transform(X[, y]) | 拟合数据并转换 |
| get_params([deep]) | 获取此估计器的参数。 |
| inverse_transform(X) | 转换回原始空间。 |
| predict(X[, copy]) | Predict targets of given samples. |
| score(X, y[, sample_weight]) | 返回预测的 R 2 R^2 R2确定系数。 |
| set_params(**params) | 设置此估计器的参数。 |
| transform(X[, Y, copy]) | 应用尺寸缩减。 |
例:
>>> from sklearn.cross_decomposition import CCA
>>> X = [[0., 0., 1.], [1.,0.,0.], [2.,2.,2.], [3.,5.,4.]]
>>> Y = [[0.1, -0.2], [0.9, 1.1], [6.2, 5.9], [11.9, 12.3]]
>>> cca = CCA(n_components=1)
>>> cca.fit(X, Y)
CCA(n_components=1)
>>> X_c, Y_c = cca.transform(X, Y)
sklearn.cross_decomposition.PLSSVD
| 参数 | 解释 |
|---|---|
| n_components:int, default=2 | 要保留的组件数 |
| scale:bool, default=True | 是否缩放X和Y。 |
| copy:bool, default=True | 是否在缩放前应用X和Y。如果为False,这些操作将就地执行,修改两个数组。 |
| 属性 | 解释 |
|---|---|
| x_weights_:ndarray of shape (n_features, n_components) | 每次迭代的互协方差矩阵的左奇异向量。 |
| y_weights_:ndarray of shape (n_targets, n_components) | 每个奇异交叉协方差矩阵的右交叉协方差。 |
| x_scores_:ndarray of shape (n_samples, n_components) | 变换后的训练样本。 |
| y_scores_:ndarray of shape (n_samples, n_components) | 转变后的训练目标。 |
| 方法 | 解释 |
|---|---|
| fit(X, Y) | 拟合数据 |
| fit_transform(X[, y]) | 拟合数据并转换 |
| get_params([deep]) | 获取此估计器的参数。 |
| set_params(**params) | 设置此估计器的参数。 |
| transform(X[, Y, copy]) | 应用尺寸缩减。 |
例:
>>> import numpy as np
>>> from sklearn.cross_decomposition import PLSSVD
>>> X = np.array([[0., 0., 1.],
... [1., 0., 0.],
... [2., 2., 2.],
... [2., 5., 4.]])
>>> Y = np.array([[0.1, -0.2],
... [0.9, 1.1],
... [6.2, 5.9],
... [11.9, 12.3]])
>>> pls = PLSSVD(n_components=2).fit(X, Y)
>>> X_c, Y_c = pls.transform(X, Y)
>>> X_c.shape, Y_c.shape
((4, 2), (4, 2))
1.9. 朴素贝叶斯
朴素贝叶斯方法是基于贝叶斯定理的一组有监督学习算法,即“简单”地假设每对特征之间相互独立。 给定一个类别 y 和一个从 x 1 x_1 x1 到 x n x_n xn 的相关的特征向量, 贝叶斯定理阐述了以下关系:
P ( y ∣ x 1 , … , x n ) = P ( y ) P ( x 1 , … x n ∣ y ) P ( x 1 , … , x n ) P(y \mid x_1, \dots, x_n) = \frac{P(y) P(x_1, \dots x_n \mid y)}{P(x_1, \dots, x_n)} P(y∣x1,…,xn)=P(x1,…,xn)P(y)P(x1,…xn∣y)
使用简单(naive)的假设-每对特征之间都相互独立:
P ( x i ∣ y , x 1 , … , x i − 1 , x i + 1 , … , x n ) = P ( x i ∣ y ) , P(x_i | y, x_1, \dots, x_{i-1}, x_{i+1}, \dots, x_n) = P(x_i | y) , P(xi∣y,x1,…,xi−1,xi+1,…,xn)=P(xi∣y),
对于所有的 : i :i :i 都成立,这个关系式可以简化为
P ( y ∣ x 1 , … , x n ) = P ( y ) ∏ i = 1 n P ( x i ∣ y ) P ( x 1 , … , x n ) P(y \mid x_1, \dots, x_n) = \frac{P(y) \prod_{i=1}^{n} P(x_i \mid y)}{P(x_1, \dots, x_n)} P(y∣x1,…,xn)=P(x1,…,xn)P(y)∏i=1nP(xi∣y)
由于在给定的输入中 P ( x 1 , … , x n ) P(x_1, \dots, x_n) P(x1,…,xn) 是一个常量,我们使用下面的分类规则:
P ( y ∣ x 1 , … , x n ) ∝ P ( y ) ∏ i = 1 n P ( x i ∣ y ) ⇓ y ^ = arg max y P P(y \mid x_1, \dots, x_n) \propto P(y) \prod_{i=1}^{n} P(x_i \mid y)\Downarrow\hat{y} = \arg\max_y P P(y∣x1,…,xn)∝P(y)i=1∏nP(xi∣y)⇓y^=argymaxP
( y ) ∏ i = 1 n P ( x i ∣ y ) , (y) \prod_{i=1}^{n} P(x_i \mid y), (y)i=1∏nP(xi∣y),
我们可以使用最大后验概率(Maximum A Posteriori, MAP) 来估计 P ( y ) P(y) P(y) 和 P ( x i ∣ y ) P(x_i \mid y) P(xi∣y) ; 前者是训练集中类别 y y y 的相对频率。
各种各样的的朴素贝叶斯分类器的差异大部分来自于处理 P ( x i ∣ y ) P(x_i \mid y) P(xi∣y) 分布时的所做的假设不同。
尽管其假设过于简单,在很多实际情况下,朴素贝叶斯工作得很好,特别是文档分类和垃圾邮件过滤。这些工作都要求 一个小的训练集来估计必需参数。(至于为什么朴素贝叶斯表现得好的理论原因和它适用于哪些类型的数据,请参见下面的参考。)
相比于其他更复杂的方法,朴素贝叶斯学习器和分类器非常快。 分类条件分布的解耦意味着可以独立单独地把每个特征视为一维分布来估计。这样反过来有助于缓解维度灾难带来的问题。
另一方面,尽管朴素贝叶斯被认为是一种相当不错的分类器,但却不是好的估计器(estimator),所以不能太过于重视从 predict_proba 输出的概率。
1.9.1. 高斯朴素贝叶斯【naive_bayes.GaussianNB】
GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布:
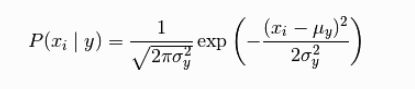
参数 σ y \sigma_y σy 和 μ y \mu_y μy 使用最大似然法估计。
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> from sklearn.naive_bayes import GaussianNB
>>> gnb = GaussianNB()
>>> y_pred = gnb.fit(iris.data, iris.target).predict(iris.data)
>>> print("Number of mislabeled points out of a total %d points : %d"
... % (iris.data.shape[0],(iris.target != y_pred).sum()))
Number of mislabeled points out of a total 150 points : 6
sklearn.naive_bayes.GaussianNB
| 参数 | 解释 |
|---|---|
| priors:array-like of shape (n_classes,) | 类的先验概率。如果指定,则不根据数据调整优先级。 |
| var_smoothing:float, default=1e-9 | 所有特征中最大方差的一部分,为计算稳定性而添加到方差中。 |
| 属性 | 解释 |
|---|---|
| class_count_:ndarray of shape (n_classes,) | 每节课观察到的训练样本数。 |
| class_prior_:ndarray of shape (n_classes,) | 每一类的概率。 |
| classes_:ndarray of shape (n_classes,) | 分类器已知的类标签 |
| epsilon_:float | 方差的绝对加和值 |
| sigma_:ndarray of shape (n_classes, n_features) | 每类特征的方差 |
| theta_:ndarray of shape (n_classes, n_features) | 每类特征的平均值 |
| 方法 | 解释 |
|---|---|
| fit(X, Y) | 拟合数据 |
| get_params([deep]) | 获取此估计器的参数。 |
| partial_fit(X, y[, classes, sample_weight]) | 对一批样品进行增量拟合。 |
| predict(X) | 对测试向量X的数组执行分类。 |
| predict_log_proba(X) | 测试向量X的返回对数概率估计。 |
| predict_proba(X) | 测试向量X的返回概率估计。 |
| score(X, y[, sample_weight]) | 返回给定测试数据和标签的平均精度。 |
| set_params(**params) | 设置此估计器的参数。 |
例:
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> Y = np.array([1, 1, 1, 2, 2, 2])
>>> from sklearn.naive_bayes import GaussianNB
>>> clf = GaussianNB()
>>> clf.fit(X, Y)
GaussianNB()
>>> print(clf.predict([[-0.8, -1]]))
[1]
>>> clf_pf = GaussianNB()
>>> clf_pf.partial_fit(X, Y, np.unique(Y))
GaussianNB()
>>> print(clf_pf.predict([[-0.8, -1]]))
[1]
1.9.2. 多项分布朴素贝叶斯【naive_bayes.MultinomialNB】
MultinomialNB 实现了服从多项分布数据的朴素贝叶斯算法,也是用于文本分类(这个领域中数据往往以词向量表示,尽管在实践中 tf-idf 向量在预测时表现良好)的两大经典朴素贝叶斯算法之一。 分布参数由每类 y 的 θ y = ( θ y 1 , … , θ y n ) \theta_y = (\theta_{y1},\ldots,\theta_{yn}) θy=(θy1,…,θyn) 向量决定, 式中 n 是特征的数量(对于文本分类,是词汇量的大小) θ y i \theta_{yi} θyi 是样本中属于类 y 中特征 i 概率 P ( x i ∣ y ) P(x_i \mid y) P(xi∣y) 。
参数 θ y \theta_y θy 使用平滑过的最大似然估计法来估计,即相对频率计数:
θ ^ y i = N y i + α N y + α n \hat{\theta}_{yi} = \frac{ N_{yi} + \alpha}{N_y + \alpha n} θ^yi=Ny+αnNyi+α
式中 N y i = ∑ x ∈ T x i N_{yi} = \sum_{x \in T} x_i Nyi=∑x∈Txi是 训练集T中特征i在类y中出现的次数, N y = ∑ i = 1 ∣ T ∣ N y i N_{y} = \sum_{i=1}^{|T|} N_{yi} Ny=∑i=1∣T∣Nyi 是类 y 中出现所有特征的计数总和。
先验平滑因子 α ≥ 0 \alpha \ge 0 α≥0 为在学习样本中没有出现的特征而设计,以防在将来的计算中出现0概率输出。 把 α = 1 \alpha = 1 α=1 被称为拉普拉斯平滑(Lapalce smoothing),而 α < 1 \alpha < 1 α<1 被称为Lidstone平滑方法(Lidstone smoothing)。
sklearn.naive_bayes.MultinomialNB
| 参数 | 解释 |
|---|---|
| alpha:float, default=1.0 | 加法(拉普拉斯/利德斯通)平滑参数(0表示无平滑)。 |
| fit_prior:bool, default=True | 是否学习先验概率。如果为False,将使用统一优先级。 |
| class_prior:array-like of shape (n_classes,), default=None | 类的先验概率。如果指定,则不根据数据调整优先级。 |
| 属性 | 解释 |
|---|---|
| class_count_:ndarray of shape (n_classes,) | 每个类观察到的训练样本数。 |
| class_log_prior_:ndarray of shape (n_classes, ) | 平滑的经验对数概率为每一类。 |
| classes_:ndarray of shape (n_classes,) | 分类器已知的类标签 |
| coef_:ndarray of shape (n_classes, n_features) | Mirrors feature_log_prob_ for interpreting MultinomialNB as a linear model. |
| feature_count_:ndarray of shape (n_classes, n_features) | 拟合期间每个(类、特征)遇到的样本数。当提供时,该值由样本重量加权。 |
| feature_log_prob_:ndarray of shape (n_classes, n_features) | 给定一类特征的经验对数概率P(x |
| intercept_:ndarray of shape (n_classes,) | Mirrors class_log_prior_ for interpreting MultinomialNB as a linear model. |
| n_features_:int | 每个样本的特征数。 |
| 方法 | 解释 |
|---|---|
| fit(X, Y) | 拟合数据 |
| get_params([deep]) | 获取此估计器的参数。 |
| partial_fit(X, y[, classes, sample_weight]) | 对一批样品进行增量拟合。 |
| predict(X) | 对测试向量X的数组执行分类。 |
| predict_log_proba(X) | 测试向量X的返回对数概率估计。 |
| predict_proba(X) | 测试向量X的返回概率估计。 |
| score(X, y[, sample_weight]) | 返回给定测试数据和标签的平均精度。 |
| set_params(**params) | 设置此估计器的参数。 |
例:
>>> import numpy as np
>>> rng = np.random.RandomState(1)
>>> X = rng.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import MultinomialNB
>>> clf = MultinomialNB()
>>> clf.fit(X, y)
MultinomialNB()
>>> print(clf.predict(X[2:3]))
[3]
1.9.3. 补充朴素贝叶斯【naive_bayes.ComplementNB】
ComplementNB实现了补充朴素贝叶斯(CNB)算法。CNB是标准多项式朴素贝叶斯(MNB)算法的一种改进,特别适用于不平衡数据集。具体来说,CNB使用来自每个类的补数的统计数据来计算模型的权重。CNB的发明者的研究表明,CNB的参数估计比MNB的参数估计更稳定。此外,CNB在文本分类任务上通常比MNB表现得更好(通常有相当大的优势)。计算权重的步骤如下:
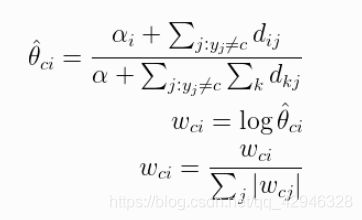
其中对不在类c中的所有记录j求和,dij可以是文档j中词语i的计数或tf-idf值,αi是就像MNB中一样的平滑超参数,同时 α = ∑ i α i \alpha = \sum_{i} \alpha_i α=∑iαi。第二个归一化解决了长记录主导MNB参数估计的问题。分类规则为:
c ^ = arg min c ∑ i t i w c i \hat{c} = \arg\min_c \sum_{i} t_i w_{ci} c^=argcmini∑tiwci
即将记录分配给补充匹配度最低的类。
sklearn.naive_bayes.ComplementNB
| 参数 | 解释 |
|---|---|
| alpha:float, default=1.0 | 加法(拉普拉斯/利德斯通)平滑参数(0表示无平滑)。 |
| fit_prior:bool, default=True | 仅用于训练集中单个类的边缘情况。 |
| class_prior:array-like of shape (n_classes,), default=None | 类的先验概率。 |
| norm:bool, default=False | 是否执行权重的第二标准化。 |
| 属性 | 解释 |
|---|---|
| class_count_:ndarray of shape (n_classes,) | 每个类观察到的训练样本数。 |
| class_log_prior_:ndarray of shape (n_classes, ) | 平滑的经验对数概率为每一类。 |
| classes_:ndarray of shape (n_classes,) | 分类器已知的类标签 |
| coef_:ndarray of shape (n_classes, n_features) | Mirrors feature_log_prob_ for interpreting MultinomialNB as a linear model. |
| feature_all_:ndarray of shape (n_features,) | 拟合期间每个特征遇到的样本数。当提供时,该值由样本重量加权。 |
| feature_count_:ndarray of shape (n_classes, n_features) | 拟合期间每个(类、特征)遇到的样本数。当提供时,该值由样本重量加权。 |
| feature_log_prob_:ndarray of shape (n_classes, n_features) | 给定一类特征的经验对数概率P(x |
| intercept_:ndarray of shape (n_classes,) | Mirrors class_log_prior_ for interpreting MultinomialNB as a linear model. |
| n_features_:int | 每个样本的特征数。 |
| 方法 | 解释 |
|---|---|
| fit(X, Y) | 拟合数据 |
| get_params([deep]) | 获取此估计器的参数。 |
| partial_fit(X, y[, classes, sample_weight]) | 对一批样品进行增量拟合。 |
| predict(X) | 对测试向量X的数组执行分类。 |
| predict_log_proba(X) | 测试向量X的返回对数概率估计。 |
| predict_proba(X) | 测试向量X的返回概率估计。 |
| score(X, y[, sample_weight]) | 返回给定测试数据和标签的平均精度。 |
| set_params(**params) | 设置此估计器的参数。 |
例:
>>> import numpy as np
>>> rng = np.random.RandomState(1)
>>> X = rng.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import ComplementNB
>>> clf = ComplementNB()
>>> clf.fit(X, y)
ComplementNB()
>>> print(clf.predict(X[2:3]))
[3]
1.9.4. 伯努利朴素贝叶斯【naive_bayes.BernoulliNB】
BernoulliNB 实现了用于多重伯努利分布数据的朴素贝叶斯训练和分类算法,即有多个特征,但每个特征 都假设是一个二元 (Bernoulli, boolean) 变量。 因此,这类算法要求样本以二元值特征向量表示;如果样本含有其他类型的数据, 一个 BernoulliNB 实例会将其二值化(取决于 binarize 参数)。
伯努利朴素贝叶斯的决策规则基于:
P ( x i ∣ y ) = P ( i ∣ y ) x i + ( 1 − P ( i ∣ y ) ) ( 1 − x i ) P(x_i \mid y) = P(i \mid y) x_i + (1 - P(i \mid y)) (1 - x_i) P(xi∣y)=P(i∣y)xi+(1−P(i∣y))(1−xi)
与多项分布朴素贝叶斯的规则不同 伯努利朴素贝叶斯明确地惩罚类 y 中没有出现作为预测因子的特征 i ,而多项分布分布朴素贝叶斯只是简单地忽略没出现的特征。
在文本分类的例子中,统计词语是否出现的向量(word occurrence vectors)(而非统计词语出现次数的向量(word count vectors))可以用于训练和使用这个分类器。 BernoulliNB 可能在一些数据集上表现得更好,特别是那些更短的文档。 如果时间允许,建议对两个模型都进行评估。
sklearn.naive_bayes.BernoulliNB
| 参数 | 解释 |
|---|---|
| alpha:float, default=1.0 | 加法(拉普拉斯/利德斯通)平滑参数(0表示无平滑)。 |
| binarize:float or None, default=0.0 | 样本特征的二值化(映射到布尔)阈值。如果None,则假定输入已经由二进制向量组成。 |
| fit_prior:bool, default=True | 仅用于训练集中单个类的边缘情况。 |
| class_prior:array-like of shape (n_classes,), default=None | 类的先验概率。 |
| 属性 | 解释 |
|---|---|
| class_count_:ndarray of shape (n_classes,) | 每个类观察到的训练样本数。 |
| class_log_prior_:ndarray of shape (n_classes, ) | 平滑的经验对数概率为每一类。 |
| classes_:ndarray of shape (n_classes,) | 分类器已知的类标签 |
| coef_:ndarray of shape (n_classes, n_features) | Mirrors feature_log_prob_ for interpreting MultinomialNB as a linear model. |
| feature_count_:ndarray of shape (n_classes, n_features) | 拟合期间每个(类、特征)遇到的样本数。当提供时,该值由样本重量加权。 |
| feature_log_prob_:ndarray of shape (n_classes, n_features) | 给定一类特征的经验对数概率P(x |
| intercept_:ndarray of shape (n_classes,) | Mirrors class_log_prior_ for interpreting MultinomialNB as a linear model. |
| n_features_:int | 每个样本的特征数。 |
| 方法 | 解释 |
|---|---|
| fit(X, Y) | 拟合数据 |
| get_params([deep]) | 获取此估计器的参数。 |
| partial_fit(X, y[, classes, sample_weight]) | 对一批样品进行增量拟合。 |
| predict(X) | 对测试向量X的数组执行分类。 |
| predict_log_proba(X) | 测试向量X的返回对数概率估计。 |
| predict_proba(X) | 测试向量X的返回概率估计。 |
| score(X, y[, sample_weight]) | 返回给定测试数据和标签的平均精度。 |
| set_params(**params) | 设置此估计器的参数。 |
例:
>>> import numpy as np
>>> rng = np.random.RandomState(1)
>>> X = rng.randint(5, size=(6, 100))
>>> Y = np.array([1, 2, 3, 4, 4, 5])
>>> from sklearn.naive_bayes import BernoulliNB
>>> clf = BernoulliNB()
>>> clf.fit(X, Y)
BernoulliNB()
>>> print(clf.predict(X[2:3]))
[3]
1.9.5. 基于外存的朴素贝叶斯模型拟合
朴素贝叶斯模型可以解决整个训练集不能导入内存的大规模分类问题。 为了解决这个问题, MultinomialNB, BernoulliNB, 和 GaussianNB 实现了 partial_fit 方法,可以动态的增加数据,使用方法与其他分类器的一样。所有的朴素贝叶斯分类器都支持样本权重。
与fit 方法不同,首次调用 partial_fit方法需要传递一个所有期望的类标签的列表。
注意:所有朴素贝叶斯模型调用 partial_fit 都会引入一些计算开销。推荐让数据块越大越好,其大小与 RAM 中可用内存大小相同。
1.10. 决策树
Decision Trees (DTs) 是一种用来 classification 和 regression 的无参监督学习方法。其目的是创建一种模型从数据特征中学习简单的决策规则来预测一个目标变量的值。
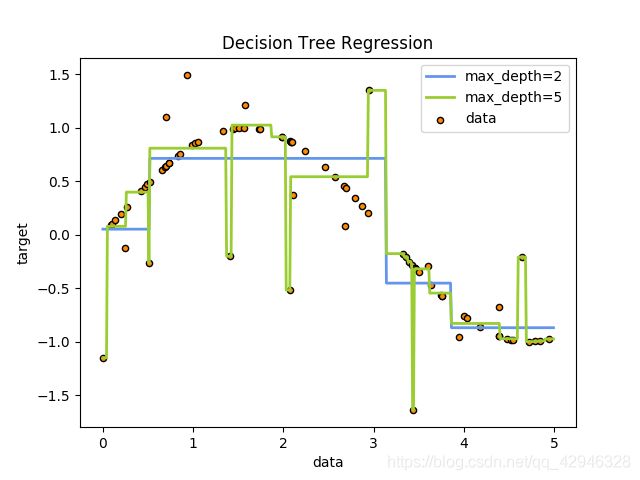
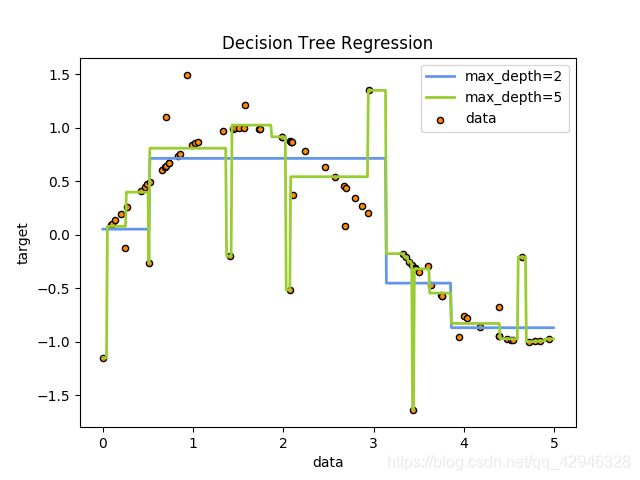
例如,在下面的图片中,决策树通过if-then-else的决策规则来学习数据从而估测数一个正弦图像。决策树越深入,决策规则就越复杂并且对数据的拟合越好。
决策树的优势:
-
便于理解和解释。树的结构可以可视化出来。
-
训练需要的数据少。其他机器学习模型通常需要数据规范化,比如构建虚拟变量和移除缺失值,不过请注意,这种模型不支持缺失值。
-
由于训练决策树的数据点的数量导致了决策树的使用开销呈指数分布(训练树模型的时间复杂度是参与训练数据点的对数值)。
-
能够处理数值型数据和分类数据。其他的技术通常只能用来专门分析某一种变量类型的数据集。详情请参阅算法。
-
能够处理多路输出的问题。
-
使用白盒模型。如果某种给定的情况在该模型中是可以观察的,那么就可以轻易的通过布尔逻辑来解释这种情况。相比之下,在黑盒模型中的结果就是很难说明清 楚地。
-
可以通过数值统计测试来验证该模型。这对事解释验证该模型的可靠性成为可能。
-
即使该模型假设的结果与真实模型所提供的数据有些违反,其表现依旧良好。
决策树的缺点包括:
- 决策树模型容易产生一个过于复杂的模型,这样的模型对数据的泛化性能会很差。这就是所谓的过拟合.一些策略像剪枝、设置叶节点所需的最小样本数或设置数的最大深度是避免出现 该问题最为有效地方法。
- 决策树可能是不稳定的,因为数据中的微小变化可能会导致完全不同的树生成。这个问题可以通过决策树的集成来得到缓解
- 在多方面性能最优和简单化概念的要求下,学习一棵最优决策树通常是一个NP难问题。因此,实际的决策树学习算法是基于启发式算法,例如在每个节点进 行局部最优决策的贪心算法。这样的算法不能保证返回全局最优决策树。这个问题可以通过集成学习来训练多棵决策树来缓解,这多棵决策树一般通过对特征和样本有放回的随机采样来生成。
- 有些概念很难被决策树学习到,因为决策树很难清楚的表述这些概念。例如XOR,奇偶或者复用器的问题。
- 如果某些类在问题中占主导地位会使得创建的决策树有偏差。因此,我们建议在拟合前先对数据集进行平衡
1.10.1. 分类【tree.DecisionTreeClassifier】
DecisionTreeClassifier 是能够在数据集上执行多分类的类,与其他分类器一样,DecisionTreeClassifier 采用输入两个数组:数组X,用 [n_samples, n_features] 的方式来存放训练样本。整数值数组Y,用 [n_samples] 来保存训练样本的类标签:。
>>> from sklearn import tree
>>> X = [[0, 0], [1, 1]]
>>> Y = [0, 1]
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)
执行通过之后,可以使用该模型来预测样本类别:
>>> clf.predict([[2., 2.]])
array([1])
另外,也可以预测每个类的概率,这个概率是叶中相同类的训练样本的分数:
>>> clf.predict_proba([[2., 2.]])
array([[ 0., 1.]])
DecisionTreeClassifier 既能用于二分类(其中标签为[-1,1])也能用于多分类(其中标签为[0,…,k-1])。使用Lris数据集,我们可以构造一个决策树,如下所示:
>>> from sklearn.datasets import load_iris
>>> from sklearn import tree
>>> iris = load_iris()
>>> clf = tree.DecisionTreeClassifier()
>>> clf = clf.fit(iris.data, iris.target)
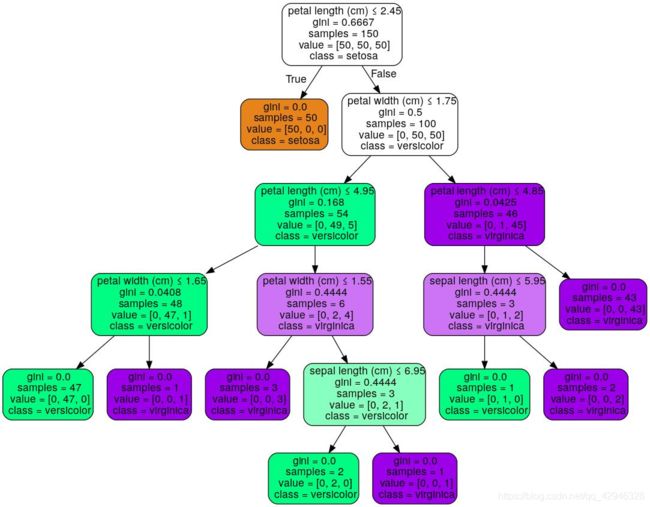
经过训练,我们可以使用 export_graphviz 导出器以 Graphviz 格式导出决策树. 如果你是用 conda来管理包,那么安装 graphviz 二进制文件和 python 包可以用以下指令安装
conda install python-graphviz
或者,可以从 graphviz项目主页下载graphviz 的二进制文件,并从 pypi 安装: Python 包装器,并安装 pip install graphviz .以下是在整个 iris 数据集上训练的上述树的 graphviz 导出示例; 其结果被保存在 iris.pdf 中:
>>> import graphviz
>>> dot_data = tree.export_graphviz(clf, out_file=None)
>>> graph = graphviz.Source(dot_data)
>>> graph.render("iris")
export_graphviz 还支持各种美化,包括通过他们的类着色节点(或回归值),如果需要,还能使用显式变量和类名。Jupyter notebook也可以自动内联式渲染这些绘制节点:
>>> dot_data = tree.export_graphviz(clf, out_file=None,
... feature_names=iris.feature_names,
... class_names=iris.target_names,
... filled=True, rounded=True,
... special_characters=True)
>>> graph = graphviz.Source(dot_data)
>>> graph
sklearn.tree.DecisionTreeClassifier
| 参数 | 解释 |
|---|---|
| criterion:{“gini”, “entropy”}, default=”gini” | 测量分割质量的函数。支持的标准是基尼杂质的“gini”和信息增益的“entropy”。 |
| splitter:{“best”, “random”}, default=”best” | 用于在每个节点上选择拆分的策略。支持的策略是“best”选择最佳分割, “random”选择最佳随机分割。 |
| max_depth:int, default=None | 树的最大深度。如果没有,则节点将展开,直到所有叶都是纯的,或者直到所有叶都包含少于min_samples_split 的值。 |
| min_samples_split:int or float, default=2 | 拆分内部节点所需的最小样本数:如果为int,则将min_samples_split 视为最小数。如果是float,那么min_samples_split是一个分数,ceil(min_samples_split * n_samples) 是每个分割的最小样本数。 |
| min_samples_leaf:int or float, default=1 | 叶节点上所需的最小样本数:如果为int,则将min_samples_split 视为最小数。如果是float,那么min_samples_split是一个分数,ceil(min_samples_split * n_samples) 是每个节点的最小样本数。 |
| min_weight_fraction_leaf:float, default=0.0 | 节点所需的(所有输入样本)权重总和的最小加权分数。未提供样本权重时,样本权重相等 |
| max_features:int, float or {“auto”, “sqrt”, “log2”}, default=None | 寻找最佳分割时要考虑的特征数量 |
| random_state:int, RandomState instance or None, default=None | 控制估计器的随机性。即使splitter设置为“best”,特征在每次分割时都是随机排列的。当max_features < n_features时,算法在每次分割时随机选取max_features,然后从中找出最优分割。但是,即使max_features=n_features,在不同的运行中找到的最佳分割可能会有所不同。在这种情况下,如果标准的改进对于几个分割是相同的,并且必须随机选择一个分割。为了在拟合过程中获得确定性行为,random_state必须固定为整数。 |
| max_leaf_nodes:int, default=None | max_leaf_nodes 以best-first方式生成树。最佳节点定义为杂质相对减少。如果没有,则叶节点的数量不受限制。 |
| min_impurity_decrease:float, default=0.0 | 如果此分裂导致杂质减少大于或等于此值,则节点将被分裂。 |
| min_impurity_split:float, default=0 | 树生长早停的阈值。如果一个节点的杂质超过阈值,它就会分裂,否则它就是叶节点。 |
| class_weight:dict, list of dict or “balanced”, default=None | 与 {class_label: weight}形式的类关联的权重。如果None,所有类都应该有权重1。对于多输出问题,可以按照与y列相同的顺序提供dict列表。 |
| ccp_alpha:non-negative float, default=0.0 | 用于最小成本复杂度修剪的复杂度参数。将选择成本复杂度最大且小于ccp_alpha的子树。默认情况下,不执行修剪。 |
| 属性 | 解释 |
|---|---|
| classes_:ndarray of shape (n_classes,) or list of ndarray | 类标签(单输出问题)或类标签数组列表(多输出问题)。 |
| feature_importances_:ndarray of shape (n_features,) | 返回特征重要性。 |
| max_features_:int | max_features的推断值。 |
| n_classes_:int or list of int | 类的数量(对于单个输出问题),或包含每个输出的类的数量的列表(对于多输出问题)。 |
| n_features_:int | 执行拟合时的特征数。 |
| n_outputs_:int | 执行拟合时的输出数。 |
| tree_:Tree instance | 基础树对象 |
| 方法 | 解释 |
|---|---|
| apply(X[, check_input]) | 返回每个样本预测为的叶的索引。 |
| cost_complexity_pruning_path(X, y[, …]) | 在最小代价复杂度修剪过程中计算修剪路径。 |
| decision_path(X[, check_input]) | 返回树中的决策路径。 |
| fit(X, y[, sample_weight, check_input, …]) | 从训练集(X,y)构建决策树分类器。 |
| get_depth() | 返回决策树的深度。 |
| get_n_leaves() | 返回决策树的叶数。 |
| get_params([deep]) | 获取此估计器的参数。 |
| predict(X[, check_input]) | 预测X的类或回归值。 |
| predict_log_proba(X) | 预测输入样本X的类对数概率。 |
| predict_proba(X[, check_input]) | 预测输入样本X的类概率。 |
| score(X, y[, sample_weight]) | 返回给定测试数据和标签的平均精度。 |
| set_params(**params) | 设置此估计器的参数。 |
例:
>>>
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.tree import DecisionTreeClassifier
>>> clf = DecisionTreeClassifier(random_state=0)
>>> iris = load_iris()
>>> cross_val_score(clf, iris.data, iris.target, cv=10)
...
...
array([ 1. , 0.93..., 0.86..., 0.93..., 0.93...,
0.93..., 0.93..., 1. , 0.93..., 1. ])
1.10.2. 回归【tree.DecisionTreeRegressor】
决策树通过使用 DecisionTreeRegressor 类也可以用来解决回归问题。如在分类设置中,拟合方法将数组X和数组y作为参数,只有在这种情况下,y数组预期才是浮点值:
>>> from sklearn import tree
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = tree.DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
array([ 0.5])
sklearn.tree.DecisionTreeRegressor
| 参数 | 解释 |
|---|---|
| criterion:{“mse”, “friedman_mse”, “mae”, “poisson”}, default=”mse” | 测量分割质量的函数。支持的标准是均方误差的“mse”,它等于作为特征选择标准的方差缩减,并使用每个终端节点的平均值最小化L2损失,“friedman_ mse”,它使用均方误差和friedman的潜在分裂改善分数,“mae”表示平均绝对误差,它使用每个终端节点的中值最小化L1损失,而“poisson”则使用泊松偏差的减少来寻找分裂。 |
| splitter:{“best”, “random”}, default=”best” | 用于在每个节点上选择拆分的策略。支持的策略是“best”选择最佳分割, “random”选择最佳随机分割。 |
| max_depth:int, default=None | 树的最大深度。如果没有,则节点将展开,直到所有叶都是纯的,或者直到所有叶都包含少于min_samples_split 的值。 |
| min_samples_split:int or float, default=2 | 拆分内部节点所需的最小样本数:如果为int,则将min_samples_split 视为最小数。如果是float,那么min_samples_split是一个分数,ceil(min_samples_split * n_samples) 是每个分割的最小样本数。 |
| min_samples_leaf:int or float, default=1 | 叶节点上所需的最小样本数:如果为int,则将min_samples_split 视为最小数。如果是float,那么min_samples_split是一个分数,ceil(min_samples_split * n_samples) 是每个节点的最小样本数。 |
| min_weight_fraction_leaf:float, default=0.0 | 节点所需的(所有输入样本)权重总和的最小加权分数。未提供样本权重时,样本权重相等 |
| max_features:int, float or {“auto”, “sqrt”, “log2”}, default=None | 寻找最佳分割时要考虑的特征数量 |
| random_state:int, RandomState instance or None, default=None | 控制估计器的随机性。即使splitter设置为“best”,特征在每次分割时都是随机排列的。当max_features < n_features时,算法在每次分割时随机选取max_features,然后从中找出最优分割。但是,即使max_features=n_features,在不同的运行中找到的最佳分割可能会有所不同。在这种情况下,如果标准的改进对于几个分割是相同的,并且必须随机选择一个分割。为了在拟合过程中获得确定性行为,random_state必须固定为整数。 |
| max_leaf_nodes:int, default=None | max_leaf_nodes 以best-first方式生成树。最佳节点定义为杂质相对减少。如果没有,则叶节点的数量不受限制。 |
| min_impurity_decrease:float, default=0.0 | 如果此分裂导致杂质减少大于或等于此值,则节点将被分裂。 |
| min_impurity_split:float, default=0 | 树生长早停的阈值。如果一个节点的杂质超过阈值,它就会分裂,否则它就是叶节点。 |
| ccp_alpha:non-negative float, default=0.0 | 用于最小成本复杂度修剪的复杂度参数。将选择成本复杂度最大且小于ccp_alpha的子树。默认情况下,不执行修剪。 |
| 属性 | 解释 |
|---|---|
| feature_importances_:ndarray of shape (n_features,) | 返回特征重要性。 |
| max_features_:int | max_features的推断值。 |
| n_features_:int | 执行拟合时的特征数。 |
| n_outputs_:int | 执行拟合时的输出数。 |
| tree_:Tree instance | 基础树对象 |
| 方法 | 解释 |
|---|---|
| apply(X[, check_input]) | 返回每个样本预测为的叶的索引。 |
| cost_complexity_pruning_path(X, y[, …]) | 在最小代价复杂度修剪过程中计算修剪路径。 |
| decision_path(X[, check_input]) | 返回树中的决策路径。 |
| fit(X, y[, sample_weight, check_input, …]) | 从训练集(X,y)构建决策树分类器。 |
| get_depth() | 返回决策树的深度。 |
| get_n_leaves() | 返回决策树的叶数。 |
| get_params([deep]) | 获取此估计器的参数。 |
| predict(X[, check_input]) | 预测X的类或回归值。 |
| predict_log_proba(X) | 预测输入样本X的类对数概率。 |
| predict_proba(X[, check_input]) | 预测输入样本X的类概率。 |
| score(X, y[, sample_weight]) | 返回预测的 R 2 R^2 R2确定系数。 |
| set_params(**params) | 设置此估计器的参数。 |
例:
>>> from sklearn.datasets import load_diabetes
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.tree import DecisionTreeRegressor
>>> X, y = load_diabetes(return_X_y=True)
>>> regressor = DecisionTreeRegressor(random_state=0)
>>> cross_val_score(regressor, X, y, cv=10)
...
...
array([-0.39..., -0.46..., 0.02..., 0.06..., -0.50...,
0.16..., 0.11..., -0.73..., -0.30..., -0.00...])
1.10.3. 多值输出问题
一个多值输出问题是一个类似当 Y 是大小为 [n_samples, n_outputs] 的2d数组时,有多个输出值需要预测的监督学习问题。
当输出值之间没有关联时,一个很简单的处理该类型的方法是建立一个n独立模型,即每个模型对应一个输出,然后使用这些模型来独立地预测n个输出中的每一个。然而,由于可能与相同输入相关的输出值本身是相关的,所以通常更好的方法是构建能够同时预测所有n个输出的单个模型。首先,因为仅仅是建立了一个模型所以训练时间会更短。第二,最终模型的泛化性能也会有所提升。对于决策树,这一策略可以很容易地用于多输出问题。 这需要以下更改:
- 在叶中存储n个输出值,而不是一个;
- 通过计算所有n个输出的平均减少量来作为分裂标准.
该模块通过在DecisionTreeClassifier和 DecisionTreeRegressor 中实现该策略来支持多输出问题。如果决策树与大小为 [n_samples, n_outputs] 的输出数组Y向匹配,则得到的估计器:
- predict 是输出n_output的值
- 在 predict_proba 上输出 n_output 数组列表
1.10.4. 复杂度分析
总体来说,用来构建平衡二叉树的运行时间为 O ( n s a m p l e s n f e a t u r e s log ( n s a m p l e s ) ) O(n_{samples}n_{features}\log(n_{samples})) O(nsamplesnfeatureslog(nsamples)) 查询时间为 O ( log ( n s a m p l e s ) ) O(\log(n_{samples})) O(log(nsamples)) 。尽管树的构造算法尝试生成平衡树,但它们并不总能保持平衡。假设子树能大概保持平衡,每个节点的成本包括通过 O ( n f e a t u r e s ) O(n_{features}) O(nfeatures) 时间复杂度来搜索找到提供熵减小最大的特征。每个节点的花费为 O ( n f e a t u r e s n s a m p l e s log ( n s a m p l e s ) ) O(n_{features}n_{samples}\log(n_{samples})) O(nfeaturesnsampleslog(nsamples)) ,从而使得整个决策树的构造成本为 O ( n f e a t u r e s n s a m p l e s 2 log ( n s a m p l e s ) ) O(n_{features}n_{samples}^{2}\log(n_{samples})) O(nfeaturesnsamples2log(nsamples)) 。
Scikit-learn提供了更多有效的方法来创建决策树。初始实现(如上所述)将重新计算沿着给定特征的每个新分割点的类标签直方图(用于分类)或平均值(用于回归)。与分类所有的样本特征,然后再次训练时运行标签计数,可将每个节点的复杂度降低为 O ( n f e a t u r e s log ( n s a m p l e s ) ) O(n_{features}\log(n_{samples})) O(nfeatureslog(nsamples)) ,则总的成本花费为 O ( n f e a t u r e s n s a m p l e s log ( n s a m p l e s ) ) O(n_{features}n_{samples}\log(n_{samples})) O(nfeaturesnsampleslog(nsamples)) 。这是一种对所有基于树的算法的改进选项。默认情况下,对于梯度提升模型该算法是打开的,一般来说它会让训练速度更快。但对于所有其他算法默认是关闭的,当训练深度很深的树时往往会减慢训练速度。
1.10.5. 实际使用技巧
- 对于拥有大量特征的数据决策树会出现过拟合的现象。获得一个合适的样本比例和特征数量十分重要,因为在高维空间中只有少量的样本的树是十分容易过拟合的。
- 考虑事先进行降维( PCA , ICA ,使您的树更好地找到具有分辨性的特征。
- 通过
export功能可以可视化您的决策树。使用max_depth=3作为初始树深度,让决策树知道如何适应您的数据,然后再增加树的深度。 - 请记住,填充树的样本数量会增加树的每个附加级别。使用
max_depth来控制输的大小防止过拟合。 - 通过使用
min_samples_split和min_samples_leaf来控制叶节点上的样本数量。当这个值很小时意味着生成的决策树将会过拟合,然而当这个值很大时将会不利于决策树的对样本的学习。所以尝试min_samples_leaf=5作为初始值。如果样本的变化量很大,可以使用浮点数作为这两个参数中的百分比。两者之间的主要区别在于min_samples_leaf保证叶结点中最少的采样数,而min_samples_split可以创建任意小的叶子,尽管在文献中min_samples_split更常见。 - 在训练之前平衡您的数据集,以防止决策树偏向于主导类.可以通过从每个类中抽取相等数量的样本来进行类平衡,或者优选地通过将每个类的样本权重 (
sample_weight) 的和归一化为相同的值。还要注意的是,基于权重的预修剪标准 (min_weight_fraction_leaf) 对于显性类别的偏倚偏小,而不是不了解样本权重的标准,如min_samples_leaf。 - 如果样本被加权,则使用基于权重的预修剪标准
min_weight_fraction_leaf来优化树结构将更容易,这确保叶节点包含样本权重的总和的至少一部分。 - 所有的决策树内部使用 np.float32 数组 ,如果训练数据不是这种格式,将会复制数据集。
- 如果输入的矩阵X为稀疏矩阵,建议您在调用
fit之前将矩阵X转换为稀疏的csc_matrix,在调用predict之前将csr_matrix稀疏。当特征在大多数样本中具有零值时,与密集矩阵相比,稀疏矩阵输入的训练时间可以快几个数量级。
1.10.6. 决策树算法: ID3, C4.5, C5.0 和 CART
所有种类的决策树算法有哪些以及它们之间的区别?scikit-learn 中实现何种算法呢?
ID3(Iterative Dichotomiser 3)由 Ross Quinlan 在1986年提出。该算法创建一个多路树,找到每个节点(即以贪心的方式)分类特征,这将产生分类目标的最大信息增益。决策树发展到其最大尺寸,然后通常利用剪枝来提高树对未知数据的泛华能力。
C4.5是 ID3 的后继者,并且通过动态定义将连续属性值分割成一组离散间隔的离散属性(基于数字变量),消除了特征必须被明确分类的限制。C4.5 将训练的树(即,ID3算法的输出)转换成 if-then 规则的集合。然后评估每个规则的这些准确性,以确定应用它们的顺序。如果规则的准确性没有改变,则需要决策树的树枝来解决。
C5.0 是 Quinlan 根据专有许可证发布的最新版本。它使用更少的内存,并建立比 C4.5 更小的规则集,同时更准确。
CART(Classification and Regression Trees (分类和回归树))与 C4.5 非常相似,但它不同之处在于它支持数值目标变量(回归),并且不计算规则集。CART 使用在每个节点产生最大信息增益的特征和阈值来构造二叉树。
scikit-learn 使用 CART 算法的优化版本。
1.10.7. 数学表达
给定训练向量 x i ∈ R n , i = 1 , … , l 和 标 签 向 量 y ∈ R l x_i \in R^n, i=1,…, l 和标签向量 y \in R^l xi∈Rn,i=1,…,l和标签向量y∈Rl。决策树递归地分割空间,例如将有相同标签的样本归为一组。
将 m 节点上的数据用 Q 来表示。每一个候选组 θ = ( j , t m ) \theta = (j, t_m) θ=(j,tm) 包含一个特征 j 和阈值 t m t_m tm 将,数据分成 Q l e f t ( θ ) Q_{left}(\theta) Qleft(θ) 和 Q r i g h t ( θ ) Q_{right}(\theta) Qright(θ) 子集。
使用不纯度函数 H() 计算 m 处的不纯度,其选择取决于正在解决的任务(分类或回归)
G ( Q , θ ) = n l e f t N m H ( Q l e f t ( θ ) ) + n r i g h t N m H ( Q r i g h t ( θ ) ) G(Q, \theta) = \frac{n_{left}}{N_m} H(Q_{left}(\theta))+ \frac{n_{right}}{N_m}H(Q_{right}(\theta)) G(Q,θ)=NmnleftH(Qleft(θ))+NmnrightH(Qright(θ))
选择使不纯度最小化的参数
θ ∗ = argmin θ G ( Q , θ ) \theta^* = \operatorname{argmin}_\theta G(Q, \theta) θ∗=argminθG(Q,θ)
在 Q l e f t ( θ ∗ ) Q_{left}(\theta^*) Qleft(θ∗) 和 Q r i g h t ( θ ∗ ) Q_{right}(\theta^*) Qright(θ∗) 上递归运算,直到达到最大允许深度, N m < min s a m p l e s N_m < \min_{samples} Nm<minsamples 或 N m = 1 N_m = 1 Nm=1。
1.10.7.1. 分类标准
对于节点 m ,表示具有 N m N_m Nm 个观测值的区域 R m R_m Rm ,如果分类结果采用值是 0,1,…,K-1 的值,让
p m k = 1 / N m ∑ x i ∈ R m I ( y i = k ) p_{mk} = 1/ N_m \sum_{x_i \in R_m} I(y_i = k) pmk=1/Nmxi∈Rm∑I(yi=k)
是节点 m 中k类观测的比例通常用来处理杂质的方法是Gini
H ( X m ) = ∑ k p m k ( 1 − p m k ) H(X_m) = \sum_k p_{mk} (1 - p_{mk}) H(Xm)=k∑pmk(1−pmk)
Cross-Entropy (交叉熵)
H ( X m ) = − ∑ k p m k log ( p m k ) H(X_m) = - \sum_k p_{mk} \log(p_{mk}) H(Xm)=−k∑pmklog(pmk)
和 Misclassification (错误分类)
H ( X m ) = 1 − max ( p m k ) H(X_m) = 1 - \max(p_{mk}) H(Xm)=1−max(pmk)
在 X m X_m Xm 训练 m 节点上的数据时。
1.10.7.2. 回归标准
如果目标是连续性的值,那么对于节点 m ,表示具有 N m N_m Nm 个观测值的区域 R m R_m Rm ,对于以后的分裂节点的位置的决定常用的最小化标准是均方差和平均绝对误差,前者使用终端节点处的平均值来最小化L2误差,后者使用终端节点处的中值来最小化 L1 误差。
Mean Squared Error (均方误差):
c m = 1 N m ∑ i ∈ N m y i H ( X m ) = 1 N m ∑ i ∈ N m ( y i − c m ) 2 c_m = \frac{1}{N_m} \sum_{i \in N_m} y_i H(X_m) = \frac{1}{N_m} \sum_{i \in N_m} (y_i - c_m)^2 cm=Nm1i∈Nm∑yiH(Xm)=Nm1i∈Nm∑(yi−cm)2
Mean Absolute Error(平均绝对误差):
y m ˉ = 1 N m ∑ i ∈ N m y i H ( X m ) = 1 N m ∑ i ∈ N m ∣ y i − y m ˉ ∣ \bar{y_m} = \frac{1}{N_m} \sum_{i \in N_m} y_i H(X_m) = \frac{1}{N_m} \sum_{i \in N_m} |y_i - \bar{y_m}| ymˉ=Nm1i∈Nm∑yiH(Xm)=Nm1i∈Nm∑∣yi−ymˉ∣
在 X m X_m Xm 训练 m 节点上的数据时。