全网最全A*算法优化策略(JPS、HPA)
ps:本文仅提供部分代码,主要描述算法思路,想法和思考
1前言
A*算法(A-Star)是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的有效算法。算法中的距离估算值与实际值越接近,最终搜索速度越快,是最常用的启发式算法。
避障碍寻路算法有很多,比如:BFS,DFS,Dijkstra等。
对于BFS,它的优点在于可以找到最优的一条路径,缺点是需要遍历整个地图。
对于DFS,它的优点在于不需要遍历整个地图,缺点在于不一定是最优路径。
对于Dijkstar,它的优点在于无差别的遍历当前最短路径,对于查找起始点到任意点的最短路径该算法很有效,缺点是:对于点对点的路径查找很浪费。
对于A*,它能很快的找到一条相对最优的路径,而且搜索的节点比前三个算法都要少。
如果DFS就像一个愣头青,一条路摸到黑的话,那么A*就是一个聪明的愣头青,它虽然也是一条路摸到黑,但是它每一步都会更加逼近终点,而不是像DFS每一步都是随机的。可以理解为A*吸收了DFS和BFS的优点,寻找到的路径优劣程度介于BFS和DFS之间。
我在公司做的一个项目,需要在1000*2000的矩阵中寻找多个最短路,故而不可能用BFS,而DFS找到的路径不可靠,所以A*是最好的选择。
2原理
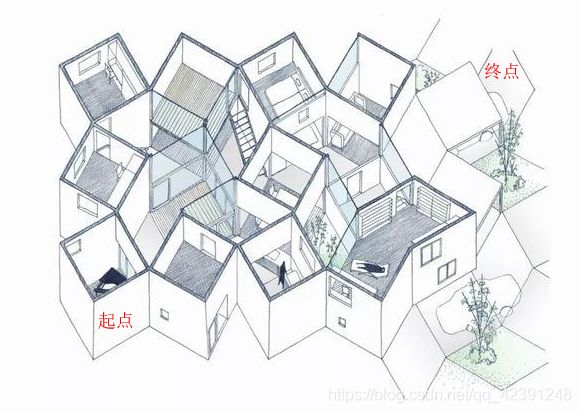
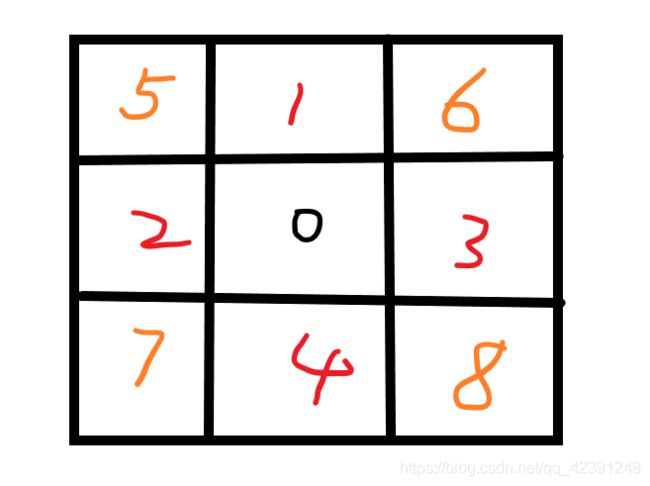
1、假设有100个房间互相连通
2、每个房间有通向隔壁房间的门
3、但有些房间的门打不开
现在你在起点,知道终点在你的东北方向,你肯定不会南辕北辙向西南方向走。你每向东,向北,向东北方向走一步,你心里都知道你里终点更近了。
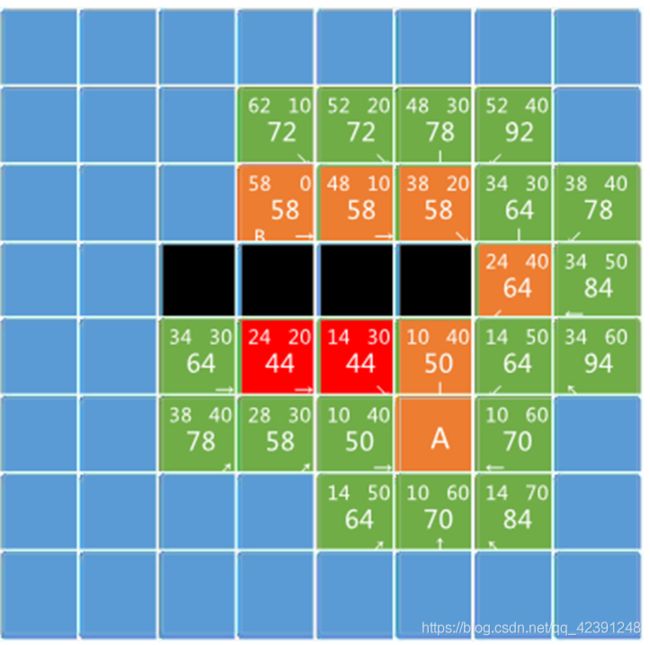
我把你心里的想法抽象成一个简单的公式:
F=G+H
G:你从起点到当前位置的实际步数
H:你预估从当前位置到终点还要走的步数
假设你在当前位置有4个其他的门可以打开,那么你会选择哪一个呢?如果是我,我会选择一个F最小优先策略,我计算一下如果我走进这四个门后,F会怎么变化,我选择F最小的一个房间走进去。这样的话,我就会离终点越来越近,最终抵达终点。
以上从起点到终点的过程,就是A*算法的简单抽象,当然A*比你想象的更加智能,相比于上面的步骤,它还会更新房间的F值,因为到一个房间可能有不同的路径,根据不同的路径走到这个房间,计算出这个房间的F值是不一样的,所以A*会选择最小的值更新该房间的F值。
3伪代码
主要搜索过程伪代码如下:
创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。
算起点的估价值;
将起点放入OPEN表;
while(OPEN!=NULL)
{
从OPEN表中取估价值f最小的节点n;
if(n节点==目标节点)
{
break;
}
for(当前节点n 的每个子节点X)
{
算X的估价值;
if(X in OPEN)
{
if( X的估价值小于OPEN表的估价值 )
{
把n设置为X的父亲;
更新OPEN表中的估价值; //取最小路径的估价值
}
}
if(X inCLOSE)
{
if( X的估价值小于CLOSE表的估价值 )
{
把n设置为X的父亲;
更新CLOSE表中的估价值;
把X节点放入OPEN //取最小路径的估价值
}
}
if(X not inboth)
{
把n设置为X的父亲;
求X的估价值;
并将X插入OPEN表中; //还没有排序
}
}//end for
将n节点插入CLOSE表中;
按照估价值将OPEN表中的节点排序; //实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。
}//end while(OPEN!=NULL)
保存路径,即 从终点开始,每个节点沿着父节点移动直至起点,这就是你的路径ps:以下内容请您在深刻理解A*并使用过A*后阅读。
4优化A*
优化A*一般从以下四个方面着手
openlist(开放集合)
getNeighbour(获取当前节点的邻居节点)
F=G+H+C(启发式函数)
map(地图)
4.1openlist 优化
4.1.1、通过优化openlist提升A*的速度
对于经典A*算法,以下针对openlist的5个操作必不可少:
添加操作:将节点添加到openlist中
删除操作:将节点从openlist中删除
获取长度:获取openlist中节点的个数
判断是否存在:判断某个节点是否已经保存在openlist中
排序:对openlist根据每个节点F的值从小到大排序
如果我们能把这五个操作的时间复杂度都降下来,那么就可以提升A*的速度
优化策略:
使用优先队列
优先队列各操作的时间复杂度如下:
添加操作:O(logn)
删除操作:O(logn)
获取长度:O(1)
判断是否存在:O(1)
排序:O(logn)
优先队列(C#)链接
4.1.2、通过优化openlist改变A*的路径
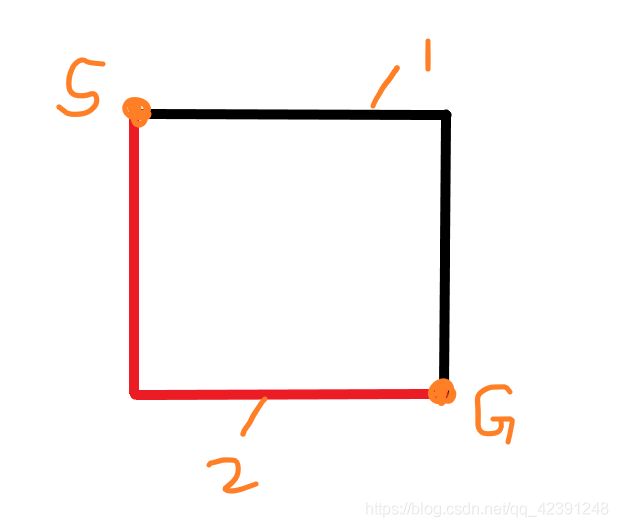
请看下面的图片,假设只要求走直线,不能走斜线,从S到G有很多种走法,下图展示了其中的两种,这两种走法都是合理的,他们实际走的路径长度是相同的。
但是我们根据实际业务的不同,会想要不同的结果。这两种走势其实和openlist有一定的关系。其中涉及到openlist的排序问题。
优化策略:
如果openlist的排序是稳定的,第一次使用A*走出了路径1,那么下一次使用A*也会走出路径1。
如果openlist的排序不稳定,那么从S到G的路径,多次使用A*的结果是不一样的。可能第一次跑出来路径1,第二次就跑出来路径2
What is 稳定的排序?
当openlist的排序是稳定时,那么先后进入open队列的节点F1=10(向右走),F2=10(向下走),一定F1会先被取出来,这样每次使用A*获取到的路径也是稳定的。
当排序不稳定时,那么可能是F2被先取出来。
4.2getNeighbour优化
getNeighbour即获取邻居节点。这个函数相当于A*的眼界。
4.2.1增加路径的随机性
我们通常获取邻居的时候,会把获取邻居的顺序写死,比如我们获取周围四个邻居(上下左右),那么A*就会优先向上试探,这样就导致无意中把向上走这个策略定为优先级最高的策略。
下面这两种路径的长度是一样的,A*会跑出路径1(因为A*会优先向上试探)。
优化策略:
有时候我们为了消除获取邻居的优先次序,会在获取邻居的时候加上概率。
比如上下左右这四种邻居的排列有6种,可以设定每种排列的结果概率为16.6%。
即16.6%的概率,获取的邻居为上下左右;
16.6%的概率,获取的邻居为左右上下;
。。。。。。
4.2.2寻找更优路径
对该函数常见的实现有:
1、获取周围4个邻居(1,2,3,4)
此时A*只会向这四个方向走
2、获取周围8个邻居(1,2,3,4,5,6,7,8)
此时A*会向8个方向走
优化策略:
根据上图,A*的眼界最多也就8个视野,如果你想让A*看的更远,可以在扩大A*眼界范围,也可以是周围两圈,三圈等等。当然,眼界越大,就意味着A*要计算的节点也就越多,A*的速度一定会变慢,优点是可以让A*找到更优的路径。
4.2.3JPS(Jump Point Search)
JPS跳点搜索算法,这是A*的一个变种,其核心就是优化了A*的getNeighbour函数。
JPS只支持允许走斜线的情况,JPS只支持允许走斜线的情况,JPS只支持允许走斜线的情况。重要的事情说三遍!如果你的需求不想要走斜线,那么就不要考虑JPS了。
JPS相对于A*有很多优点,最重要的就是寻路的速度大幅提升。
JPS通过减少邻居节点来提升速度。
例如在无遮挡情况下(往往会有多条等价路径),而我们希望起点到终点实际只取其中一条路径,而该路径外其它节点可以没必要放入openlist(不希望加入没必要的邻居)。
在此我对JPS是如何跳点搜索不做过多的陈述,只简单的介绍其思路。
优化策略:
对邻居节点进行剪枝,删去不必要的邻居。
是不是感觉听君一席话,如听一席话,上次看到这句话的时候还是上次!想了解JPS可以百度搜索,也可以下载源码:JPS跳点搜索源码(C#)
4.3F=G+H+C启发式优化
启发式是A*最核心的部分,可以说是A*的大脑,它指导着A*下一步的走向。
4.3.1减少拐点
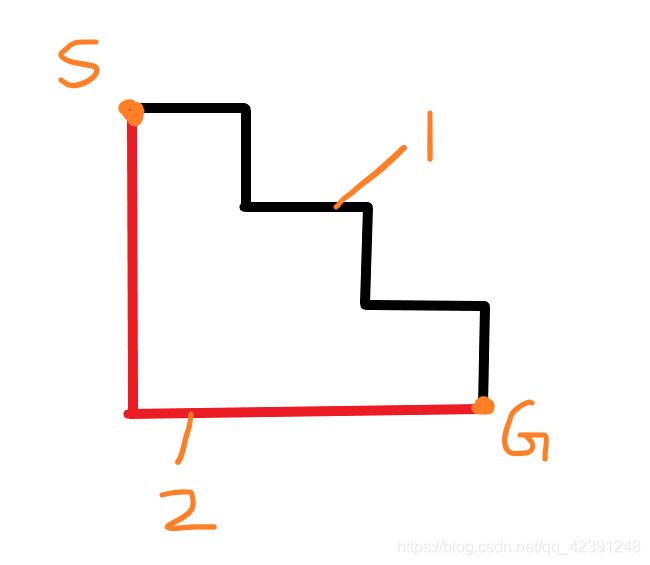
我做项目的时候,有一个需求就是减少拐点。下图路径1和路径2的长度是一样的,但是我更希望A*走出路径2。
怎么才能控制A*呢?刚才我就说了,启发式是A*的大脑,我们当然要给A*的大脑传达我们要减少拐点的意思。
在来看A*的启发式:
F=G+H+C
G:该点到起点的实际路径长度
H:该点到终点估算的估计长度
C:从当前节点走到该点的格外代价
你可以在C(额外代价)上做文章。可以通过判断从当前节点到该点是否拐弯去增加F的值。
代码如下:
///
/// 额外代价
///
/// 当前节点
/// 邻居节点
/// 终点
/// 优化策略:
如果A*拐弯,通过增大C的值来增大F的值。
加C函数的时机也很重要,我一般把C函数加在G函数上,即在计算邻居节点的G函数时,就加上C函数。
4.3.2可穿障碍物
在公司做项目时,有一个需求是:有些有障碍物的地方是可以走的,但是尽量不要从障碍物上走。这就是所谓的可穿障碍物。
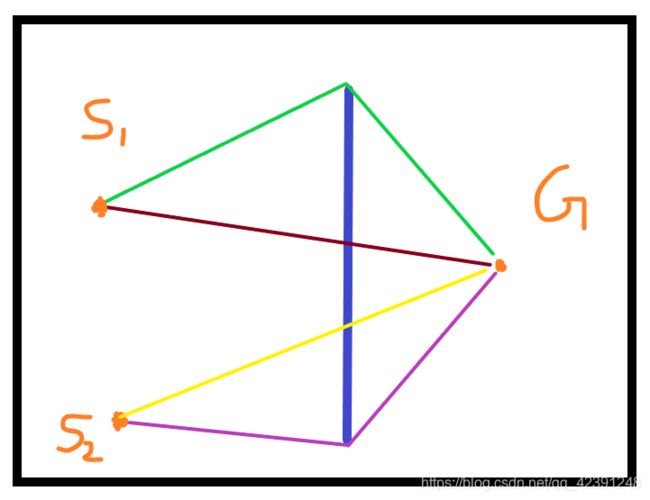
下图有四个路径,棕色和紫色是我们想要的路径。
可以这样理解:
S1到G,穿越障碍物可以让A*少走1000m(假设打车走1000m需要花10元钱),而穿越障碍物只需要花5块钱,那么A*当然会选择穿越障碍物,因为更划算了。
S2到G,穿越障碍物可以让A*少走1000m(假设打车走400m需要花4元钱),而穿越障碍物却需要花5块钱,那么A*当然会选择多走400m,因为更划算了。
说到底,A*就是一个小财迷啊!
优化策略:
在C函数在判断邻居节点是否是障碍物,如果是障碍物,就增加C的值,从而达到增加F值的目的。
PS:对于F函数来说,如果你对A*要求太高,既要它少拐点,又要它不穿越障碍物,它可能会实现,但是有时候这两个需求是互相冲突的,就导致F函数值的混乱,使得A*走出非常奇怪的路线。A*只是一个可爱的小孩子,我们不能对他要求太高哦!
4.4Map矩阵优化
map可以说是A*的人生地图,在map上,A*诞生(起点),随着启发式大脑的计算,预测着对未来的期望,一步一步走向死亡(终点),它的人生轨迹就是A*在map上路径的体现。
4.4.1通过控制维度提升速度
最常用的map就是二维矩阵了,也是图表达的最简单的数据结构。
矩阵越大,意味着数据越多,A*要搜索的范围就可以越大,A*搜索的时间也就越长。所以矩阵的大小是降低A*搜索时间最直接的因素。
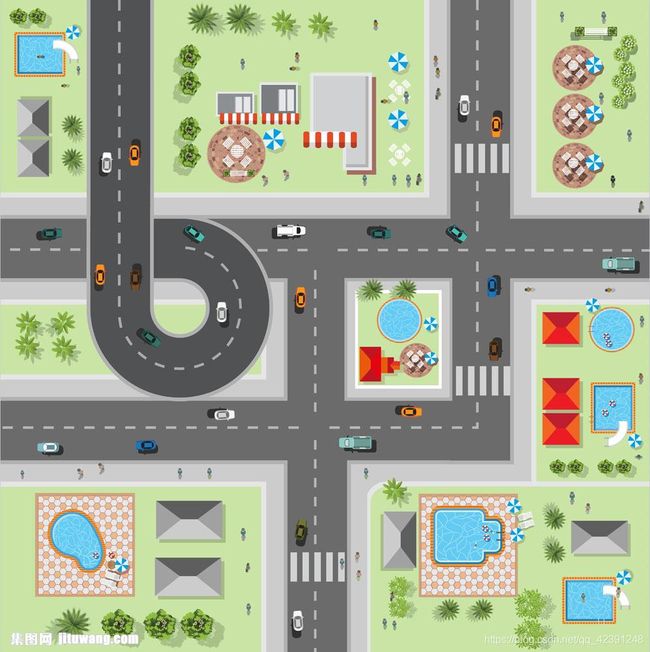
比如现实生活中100km*100km的城镇,城镇里面有大小不一的房子,街道等。我们想要将它映射成二维矩阵,想象成一个个的像素,那么问题来了:一个像素对应现实世界的长度是多少合适呢?
如果我们定义一个像素1mm,那么100km*100km就映射成100000000*100000000的二维矩阵。可以想象这个矩阵有多大,让你从左下角使用A*跑到右上角,获得的路径最少就包含200000000个点,你可能计算个1天也算不出来这个路径。
所以我们定义地图一个像素的大小是需要根据实际情况实际分析的。比如这个城镇,我们定义一个像素为1000m*1000m,虽然我们让地图的维度增大了,但是这个地图就会失真,很明显一个小车才1-2m长,1000m*1000m是无法表达出小车的长度。我会定义一个像素为1m*1m,这样我们就能表达出这个城镇所以的元素。
4.4.2分层优化提升速度--HPA
分层优化也是A*经典的优化策略了,其思想通俗点说就是对map做一个预处理。
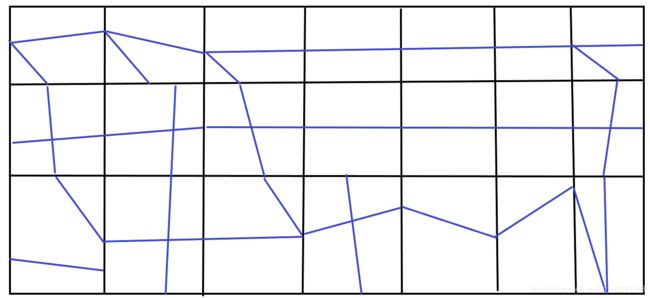
每个块可以理解为一个map,下面有3*7个map,每个map在边界上有多个出口和入口,蓝色即表示从一个口到另一个口有通路。
预处理的意思就是:在每个map中,我们使用A*计算出从起点到终点的路径,把路径提前记录下来。然后将3*7个小map拼凑成一个大map,这样每个块的路径已经存在,就不需要把map的维度降的很低了。这个方法适用于map很大的情况。
比如我们想要从北京的一个路口导航到郑州的一个路口。
优化策略:
我们先预处理中国所有城市内的所有路径,然后以城市为一个维度,计算从北京到郑州的路径。然后在将城市内的路径细化到北京到郑州,计算出实际路径。
根据这个策略,我们甚至可以很快的计算出中国北京市到北极的路径,甚至到M78星云的最短路径!
HPA*这个是HPA的实现git链接,是使用unity开发的C#代码
HPA*论文