A-Star算法探索和实现(二)
本篇摘要
上一篇我们完成了A-Star算法的基本实现,在无障碍的情况下去寻找最佳路径,而在本篇我们将在此基础上增加障碍物,让算法能够在有障碍物的条件下去寻找到最佳路径。
思路猜测
我们需要考虑以下几个问题:
第一,我们知道Node类对应的是网格单元,而每个障碍物需要对应一个网格单元,那么如何选择生成障碍物的Node?
第二,在视图层的Grid类中,如何呈现生成的障碍物?
第三,生成障碍物后,SearchPath类中寻找路径的方法需要作出哪些改变?
解决思路
根据“思路猜测”,我们提出以下解决思路:
(一)第一个问题的解决思路
我们可以给Node类添加一个nodeTag属性,并且设置将该属性设定为枚举类型,分为可通过的Node为PATHNODE,障碍物的Node为BLOCKNODE。首先我们进行障碍物Node的生成,我们需要告诉生成方法需要生成的障碍物的数量p_count,在生成方法中需要对Node作一个简单的判断,如果Node不为起始点Node和终点Node才存入Node集,然后返回生成好的Node集,依次遍历Node集,并将每个Node的nodeTag设置为BLOCKNODE。
(二)第二个问题的解决思路
我们可以通过Grid中的Mark方法来对障碍物Node进行标记,以此表示当前Node为不可通过的障碍物。
(三)第三个问题的解决思路
在SearchPath查找路径的方法中,我们需要对当前Node可前往的下一步Node集添加一个筛选条件,该条件以Node的nodeTag为判断条件,以此排除障碍物Node。
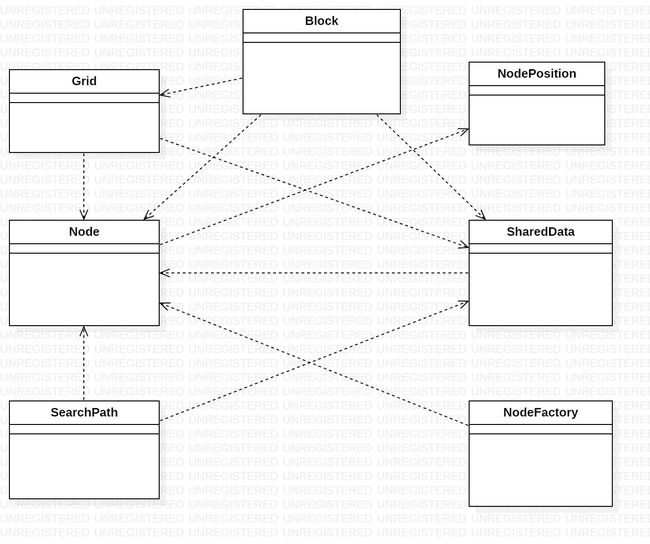
示例代码UML图
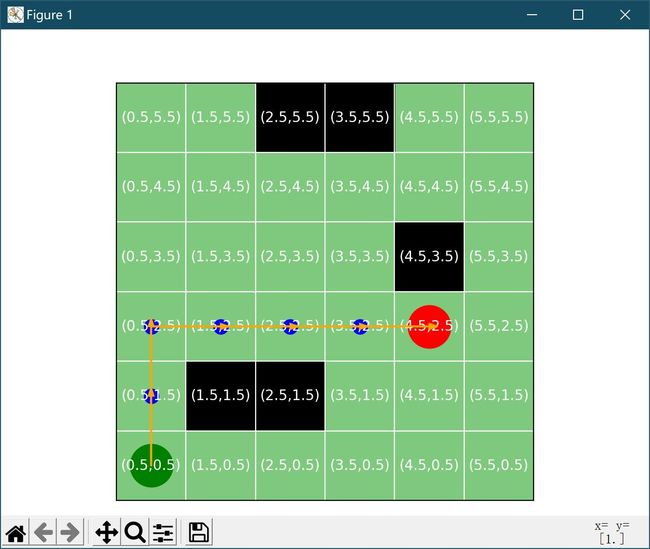
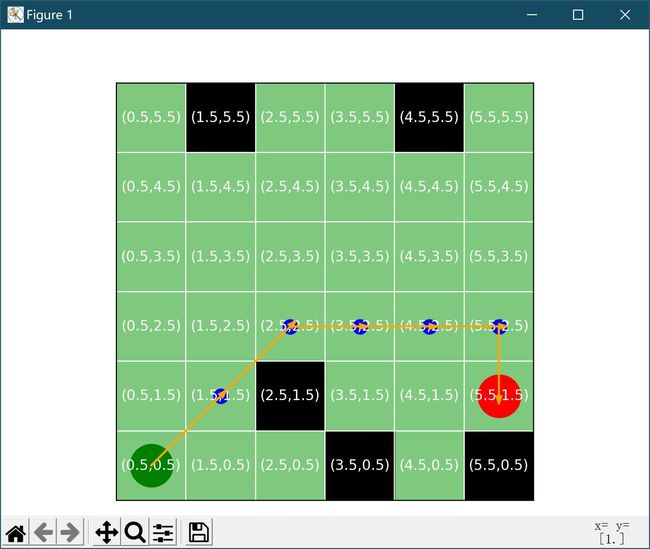
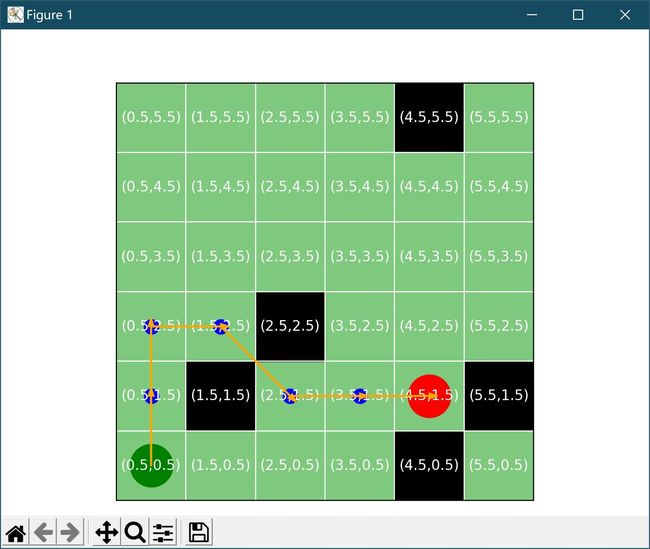
效果截图
(绿色圆点是起始点,黑色方块是障碍物,蓝色小圆点是路径,红色圆点是终点)
代码示例(Python)
Grid.py
import matplotlib.pyplot as pp
import numpy as np
from myCodes import SharedData as sd
from myCodes import Node as node
# 视图的构建和绘制
class Grid:
# 横纵坐标轴的刻度标记
__xLabels = []
__yLabels = []
# 网格单元格的信息
__data = None
# 是否完成初始化
__isInit = False
def __init__(self, p_rowsCount=6, p_colsCount=6):
if self.__isInit is False:
# 网格的行列数
self.__rowsCount = p_rowsCount
self.__colsCount = p_colsCount
# 将网格的行列数设置为共享信息
sd.SharedData.rowsCount = self.__rowsCount
sd.SharedData.colsCount = self.__colsCount
# Node工厂
self.__nodeFactory = node.NodeFactory()
# 将起始点Node和终点Node设置为共享信息
v_startNode = self.__nodeFactory.GetStartNode()
sd.SharedData.startNode = v_startNode
v_endNode = self.__nodeFactory.GetEndNode()
sd.SharedData.endNode = v_endNode
self.__isInit = True
# 绘制图形
def Draw(self):
"""绘制图形"""
# 获取坐标轴实例
v_ax = pp.gca()
self._AxisSet(v_ax)
self._GridValueSet(v_ax)
# 将数据以二维图片的形式进行显示
v_ax.imshow(self.__data, cmap='Accent', aspect='equal', vmin=0, vmax=255)
# 标记起始点和终点
self.Mark(sd.SharedData.startNode, 30, 'go')
self._PathNodeSet()
self.Mark(sd.SharedData.endNode, 30, 'ro')
# 布置网格线
pp.grid(visible=True, color='w')
pp.tight_layout()
pp.show()
# 标记所查找到的路径
def _PathNodeSet(self):
v_pathNodes = sd.SharedData.pathNodes
v_length = len(v_pathNodes)
for i in range(v_length):
if 0 < i < v_length - 1:
self.Mark(v_pathNodes[i], 10, 'bo')
self._Arrow(v_pathNodes[i - 1], v_pathNodes[i])
elif i == v_length - 1:
self._Arrow(v_pathNodes[i - 1], v_pathNodes[i])
# 标记方法
@classmethod
def Mark(cls, p_node: node.Node, p_marksize: int, p_fmt: str):
"""
标记Node
**p_node**:表示待标记的Node
**p_marksize**:表示标记的尺寸大小
**p_fmt**:表示颜色和图形的样式描述
"""
v_x = p_node.nodePos.x
v_y = p_node.nodePos.y
pp.plot(v_x, v_y, p_fmt, markersize=p_marksize, zorder=1)
# 箭头指向方法
def _Arrow(self, p_firstNode, p_secondNode):
v_dx = p_secondNode.nodePos.x - p_firstNode.nodePos.x
v_dy = p_secondNode.nodePos.y - p_firstNode.nodePos.y
pp.arrow(p_firstNode.nodePos.x, p_firstNode.nodePos.y, v_dx, v_dy, color='orange', width=0.01, head_width=0.08,
zorder=3)
# 坐标轴设置
def _AxisSet(self, p_ax):
v_ax = p_ax
for i in range(1, self.__colsCount + 1):
self.__xLabels.append(str(i))
for i in range(1, self.__rowsCount + 1):
self.__yLabels.append(str(i))
# 隐藏刻度线
v_ax.tick_params(left=False, bottom=False, top=False, right=False)
# 生成Image Data
v_low = 1
if self.__rowsCount > self.__colsCount:
v_high = self.__rowsCount
else:
v_high = self.__colsCount
self.__data = np.random.randint(v_low, v_high, size=(self.__rowsCount + 1, self.__colsCount + 1))
# 设置横纵坐标轴的范围
pp.xlim(1, self.__colsCount)
pp.ylim(1, self.__rowsCount)
# 设置坐标轴的刻度标记
v_ax.set_xticks(np.arange(self.__colsCount), labels=self.__xLabels, visible=False)
v_ax.set_yticks(np.arange(self.__rowsCount), labels=self.__yLabels, visible=False)
# 设置坐标轴的横纵轴比例相等
v_ax.set_aspect('equal')
# 网格内容设置
def _GridValueSet(self, p_ax):
v_ax = p_ax
for i in range(self.__rowsCount + 1):
for j in range(self.__colsCount + 1):
v_str = '(' + str(i + 0.5) + ',' + str(j + 0.5) + ')'
v_ax.text(i + 0.5, j + 0.5, v_str, ha='center', va='center', color='w')Node.py
import random
from enum import Enum, unique
from myCodes import SharedData as sd
# Node坐标类
class NodePosition:
def __init__(self, p_x: float = 1, p_y: float = 1):
self.x = p_x
self.y = p_y
def __str__(self):
return '[' + str(self.x) + ',' + str(self.y) + ']'
# Node标签
@unique
class NodeTag(Enum):
PATHNODE = 1
BLOCKNODE = 2
# Node类
class Node:
def __init__(self, p_nodeName: str, p_nodePos: NodePosition):
self.nodeName = p_nodeName
self.nodePos = p_nodePos
# f=g+h,g代表从上一个点到该点的代价和,h代表从该点到终点的代价和,f代表总权值weight
self.f: int = 0
self.g: int = 0
self.h: int = 0
# Node的标签,用于判断是否为不可到达的Node,
self.tag = NodeTag.PATHNODE
# 设置Node的权值
def SetWeight(self, p_f: int, p_g: int, p_h: int):
self.f = p_f
self.g = p_g
self.h = p_h
def __str__(self):
return '{nodeName:' + self.nodeName + ',nodePos:' + str(self.nodePos) + ',f=' + str(self.f) + ',g=' + str(
self.g) + ',h=' + str(self.h) + '}'
def __eq__(self, other):
if other is not None and self.nodePos.x == other.nodePos.x and self.nodePos.y == other.nodePos.y:
return True
return False
# Node工厂,用来创建和获取起始点Node和终点Node
class NodeFactory:
__isCreateEndNode = False
__isCreateStartNode = False
__startNode: Node
__endNode: Node
# Node名称索引
__nameIndex = 1
# GenerateOneNode的Node索引
__rowIndex = 1
__colIndex = 1
__generateCount = 0
def __init__(self):
pass
# 获取起始点Node
def GetStartNode(self):
"""获取起始点Node"""
if self.__isCreateStartNode is False:
self._CreateStartNode()
return self.__startNode
# 创建起始点Node
def _CreateStartNode(self):
v_nodePos = NodePosition(0.5, 0.5)
self.__startNode = Node('StartNode', v_nodePos)
self.__isCreateStartNode = True
# 获取终点Node
def GetEndNode(self):
"""获取终点Node"""
if self.__isCreateEndNode is False:
self._CreateEndNode()
return self.__endNode
# 创建终点Node
def _CreateEndNode(self):
v_startNode = sd.SharedData.startNode
v_node = v_startNode
while v_node == v_startNode:
v_node = self.GenerateOneNode('EndNode', p_isRandom=True)
self.__endNode = v_node
self.__isCreateEndNode = True
# 生成指定数量的非重复Node集
def GenerateNodes(self, p_count, p_isRandom=False):
"""
生成指定数量的非重复Node集
**p_count**:生成的Node的数量
**p_isRandom**:是否随机生成,默认为False
"""
v_list = []
v_index = 1
v_startNode = sd.SharedData.startNode
v_endNode = sd.SharedData.endNode
while len(v_list) < p_count:
v_node = self.GenerateOneNode('Node' + str(v_index), p_isRandom=p_isRandom)
if v_node is None:
break
else:
v_isRepeat = NodeCheck.RepeatCheck(v_list, v_node)
if v_isRepeat is False and v_node != v_startNode and v_node != v_endNode:
v_list.append(v_node)
v_index += 1
return v_list
# 生成一个指定名称的Node
def GenerateOneNode(self, p_name: str, p_isRandom=False):
"""
随机生成一个指定名称的Node
**p_name**:生成的Node的名称
**p_isRandom**:是否随机生成,默认为False,若为True则将按照起始点从左至右&从下至上的顺序生成
**注意**:当该方法生成完当前网格的所有Node后会进行重置并返回None,请保持对该方法的返回值是否为None的判断,避免陷入死循环
"""
v_rowsCount = sd.SharedData.rowsCount
v_colsCount = sd.SharedData.colsCount
v_x = 0.5
v_y = 0.5
if p_isRandom:
v_i = random.randint(0, v_rowsCount - 1)
v_x = v_i + 0.5
v_i = random.randint(0, v_colsCount - 1)
v_y = v_i + 0.5
else:
if self.__colIndex < v_colsCount:
if self.__rowIndex > v_rowsCount:
self.__rowIndex -= v_rowsCount
self.__colIndex += 1
v_x = (self.__rowIndex - 1) + 0.5
v_y = (self.__colIndex - 1) + 0.5
self.__rowIndex += 1
self.__generateCount += 1
else:
if self.__rowIndex <= v_rowsCount:
v_x = (self.__rowIndex - 1) + 0.5
v_y = (self.__colIndex - 1) + 0.5
self.__rowIndex += 1
self.__generateCount += 1
else:
self.__rowIndex = 1
self.__colIndex = 1
if self.__generateCount > v_rowsCount * v_colsCount:
self.__generateCount = 0
return None
v_nodePos = NodePosition(v_x, v_y)
v_node = Node(p_name, v_nodePos)
return v_node
# 获取当前Node下一步可以前往的Node集
def GenerateNextNodes(self, p_node):
"""
获取当前Node下一步可以前往的Node集
**p_node**:当前Node
"""
if p_node is not None:
v_p = p_node.nodePos
v_posList = [(v_p.x - 1, v_p.y), (v_p.x - 1, v_p.y + 1), (v_p.x, v_p.y + 1), (v_p.x + 1, v_p.y + 1),
(v_p.x + 1, v_p.y), (v_p.x + 1, v_p.y - 1), (v_p.x, v_p.y - 1), (v_p.x - 1, v_p.y - 1)]
v_nameList = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
v_list = []
for i in range(len(v_posList)):
v_nodeName = v_nameList[i] + str(self.__nameIndex)
v_nodePos = NodePosition(v_posList[i][0], v_posList[i][1])
v_node = Node(v_nodeName, v_nodePos)
v_list.append(v_node)
self.__nameIndex += 1
return v_list
return None
class NodeCheck:
# 判断列表中是否存在当前Node
@classmethod
def RepeatCheck(cls, p_list: list, p_node: Node):
"""判断列表中是否存在当前Node"""
if p_list is not None:
for n in p_list:
if n == p_node:
return True
return False
# 判断当前Node是否超出了网格限定
@classmethod
def OutOfRange(cls, p_node: Node):
"""判断当前Node是否超出了网格限定"""
v_minX = 0.5
v_minY = 0.5
v_maxX = (sd.SharedData.rowsCount - 1) + 0.5
v_maxY = (sd.SharedData.colsCount - 1) + 0.5
v_x = p_node.nodePos.x
v_y = p_node.nodePos.y
if v_minX <= v_x <= v_maxX and v_minY <= v_y <= v_maxY:
return False
return TrueBlock.py
from myCodes import Grid as grid
from myCodes import Node as node
from myCodes import SharedData as sd
# 用于生成阻碍物
class Block:
def __init__(self, p_blcokCount: int):
"""
:param p_blcokCount: 生成的障碍物的数量
"""
self.__blockCount = p_blcokCount
self.__nodeFactory = node.NodeFactory()
# 用于生成Block
def Create(self):
v_list = self._SelectNode()
v_list = self._GenerateBlock(v_list)
sd.SharedData.blockNodes = v_list
self._MarkBlockNode(v_list)
# 获取生成Block的Node或Node集
def _SelectNode(self):
v_list = self.__nodeFactory.GenerateNodes(self.__blockCount, p_isRandom=True)
return v_list
# 生成Block
def _GenerateBlock(self, p_list):
if p_list is not None:
v_list = p_list
for n in v_list:
n.nodeTag = node.NodeTag.BLOCKNODE
return v_list
return None
# 标记生成Block的Node
def _MarkBlockNode(self, p_list):
if p_list is not None:
for n in p_list:
grid.Grid.Mark(n, 49, 'ks')SearchPath.py
from myCodes import SharedData as sd
from myCodes import Node as node
# 查找最佳路径
class SearchPath:
# 对角线移动一格的代价
__diagonalCost = 14
# 上下或左右移动一格的代价
__nonDiagonalCost = 10
__nodeFactory: node.NodeFactory
__currentNode: node.Node
# 是否完成了初始化
__isInit = False
__openList = []
__closeList = []
# 网格行列数
__rowsCount = 0
__colsCount = 0
# x和y的最小值
__minX = 0.5
__minY = 0.5
# x和y的最大值
__maxX = 0
__maxY = 0
# 终点Node
__endNode: node.Node
def __init__(self):
if self.__isInit is False:
self.__nodeFactory = node.NodeFactory()
self.__currentNode = sd.SharedData.startNode
self.__openList.append(self.__currentNode)
self.__rowsCount = sd.SharedData.rowsCount
self.__colsCount = sd.SharedData.colsCount
self.__maxX = self.__rowsCount - 0.5
self.__maxY = self.__colsCount - 0.5
self.__endNode = sd.SharedData.endNode
self.__isInit = True
# 查找最佳路径
def Search(self, p_isPrint=False):
"""
查找最佳路径
p_isPrint:是否在控制台打印路径Node集信息,默认为False
"""
while self._UpdateCurrentNode():
# 获取currentNode下一步可以前往的Node,并将它们保存在一个临时列表v_list中
v_list = self.__nodeFactory.GenerateNextNodes(self.__currentNode)
v_list = self._NodeCheck(v_list)
v_list = self._CalculateWeight(v_list)
v_list = self._SortNode(v_list)
self._AddNode(v_list)
sd.SharedData.pathNodes = self.__closeList
if p_isPrint:
self._PrintPath()
# 检查临时列表p_list中哪些Node不符合要求,保留符合要求的节点
def _NodeCheck(self, p_list):
if p_list is not None:
v_list1 = []
v_list2 = []
for n in p_list:
if node.NodeCheck.OutOfRange(n) is False:
v_list1.append(n)
for n in v_list1:
v_isInOpenList = node.NodeCheck.RepeatCheck(self.__openList, n)
v_isInCloseList = node.NodeCheck.RepeatCheck(self.__closeList, n)
v_isInBlockList = node.NodeCheck.RepeatCheck(sd.SharedData.blockNodes, n)
if v_isInOpenList is False and v_isInCloseList is False and v_isInBlockList is False:
v_list2.append(n)
return v_list2
return None
# 计算临时列表p_list中每个Node的权值
def _CalculateWeight(self, p_list):
if p_list is not None:
v_list = p_list
v_startNodeX = self.__currentNode.nodePos.x
v_startNodeY = self.__currentNode.nodePos.y
v_endNodeX = self.__endNode.nodePos.x
v_endNodeY = self.__endNode.nodePos.y
for n in v_list:
v_x = n.nodePos.x
v_y = n.nodePos.y
if v_x == v_y:
v_g = abs((v_x - v_startNodeX)) * self.__diagonalCost
if v_endNodeX == v_endNodeY:
v_h = abs((v_endNodeX - v_x)) * self.__diagonalCost
else:
v_h = abs((v_endNodeX - v_x)) * self.__nonDiagonalCost + abs(
(v_endNodeY - v_y)) * self.__nonDiagonalCost
else:
v_g = abs((v_x - v_startNodeX)) * self.__nonDiagonalCost + abs(
(v_y - v_startNodeY)) * self.__nonDiagonalCost
v_h = abs((v_endNodeX - v_x)) * self.__nonDiagonalCost + abs(
(v_endNodeY - v_y)) * self.__nonDiagonalCost
v_f = v_g + v_h
n.SetWeight(v_f, v_g, v_h)
return v_list
return None
# 根据临时列表p_list中每个Node的权值进行排序,权值越小越接近列表尾
def _SortNode(self, p_list):
if p_list is not None:
v_list = p_list
for i in range(0, len(v_list)):
for j in range(i + 1, len(v_list)):
if v_list[i].f > v_list[j].f:
v_node = v_list[i]
v_list[i] = v_list[j]
v_list[j] = v_node
return v_list
return None
# 将临时列表p_list拼接在openList的列表尾
def _AddNode(self, p_list):
if p_list is not None:
v_list = []
for i in range(len(p_list)):
v_n = p_list[i]
v_isInOpenList = node.NodeCheck.RepeatCheck(self.__openList, v_n)
v_isInCloseList = node.NodeCheck.RepeatCheck(self.__closeList, v_n)
if v_isInOpenList is False and v_isInCloseList is False:
v_list.append(v_n)
self.__openList.append(v_list[0])
return True
return False
# 打印最佳路径
def _PrintPath(self):
v_str = ''
v_length = len(self.__closeList)
for i in range(v_length):
if i < v_length - 1:
v_str += str(self.__closeList[i]) + '-->'
else:
v_str += str(self.__closeList[i])
print(v_str)
# 从openList中获取列表尾的元素,将之作为currentNode并加入closeList中,然后将其从openList中移除
def _UpdateCurrentNode(self):
if len(self.__openList) > 0:
self.__currentNode = self.__openList[0]
v_isInCloseList = node.NodeCheck.RepeatCheck(self.__closeList, self.__currentNode)
if v_isInCloseList is False:
self.__closeList.append(self.__currentNode)
del self.__openList[0]
if self.__currentNode == self.__endNode:
return False
return True
return FalseSharedData.py
from myCodes import Node as node
# 共享信息类
class SharedData:
# 网格行列数
rowsCount = 0
colsCount = 0
# 起始点Node
startNode: node.Node
# 终点Node
endNode: node.Node
# 所查找的路径Node集
pathNodes = []
# 障碍物Node集
blockNodes = []Main.py
from myCodes import SearchPath as sp
from myCodes import Grid as grid
from myCodes import Block as block
g = grid.Grid()
block.Block(5).Create()
sp.SearchPath().Search()
g.Draw()代码解说
在上一篇中,我们将代码分为了视图层和数据层两个层级,并且对视图层的Grid类,以及数据层的Node类、NodePosition类、NodeFactory类、SharedData类、SearchPath类分别进行了解说。在本篇我们又添加了两个新的成员——Block类、NodeCheck类,Block类将作为数据层家族的一员,而它将负责障碍物的生成和标记,NodeCheck类也将加入数据层,它的任务是对Node和Node集进行各种检测。除此之外我们对上一篇中的代码进行了简化,当我们编写的代码越来越多时,我们不得不考虑到代码的优化,否则当你面对一篇结构混乱、可读性低的代码时,你可能就没有心情继续编写了,这对程序员来说无疑就像是失恋一般难受,在后续我们将采用设计模式进行进一步的优化。
不过在此之前,如果你足够细心地进行了观察的话,一定会发现本篇中所存在的诸多问题。例如障碍物的生成可能出现“死胡同”的情况,这可能导致要么从起始点无法出去,要么无法进入终点;障碍物生成在对角的顶点处似乎并没有意义,这并不能阻止或影响我们到达终点;对于在周围存在障碍物时按照对角线移动是否合理,这涉及到障碍物的四个角是否能够阻止我们前行,因为在游戏场景中这可能就表现为我们半边身体从一个突出的墙体中穿了过去;有时候我们所选择的路径似乎并不是最佳路径,这说明我们获取最佳路径的方式存在漏洞,这并不是A*算法的问题,而是我们自己的问题,或者说我们获取最佳路径的方式严格上来说并算不上是标准的A*算法,这些问题我们将会在下一篇进行探讨。
下一篇将针对以上的问题进行进一步的探索和实现
如果这篇文章对你有帮助,请给作者点个赞吧!