数学建模：12 分类模型

目录

逻辑回归 logistic regression

线性概率模型（Linear Probability Model，简记LPM） 

Spss求解逻辑回归

步骤

逐步回归的设置

自变量有分类变量

预测结果差：添加平方项/交互项

过拟合现象

如何确定合适的模型：交叉验证

Fisher线性判别分析

SPSS操作

多分类问题

Fisher判别分析

Logistic回归

---

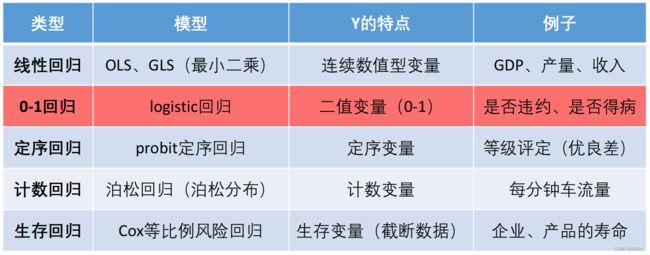
逻辑回归 logistic regression

01回归可以用逻辑回归，即对于因变量为分类变量的情况，可以使用逻辑回归进行处理：
       把 y 看成事件发生的概率，y>=0.5表示发生；y<0.5表示不发生

线性概率模型（Linear Probability Model，简记LPM） 

如果直接用之前的线性模型进行回归：

上述模型存在的问题：

1. 由于 y 只能取0/1，存在内生性问题：
   
   
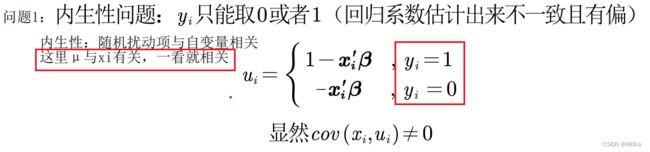
2. y_hat 即 y 的预测值的取值是概率（后面解释为什么可以把 y_hat 理解为 “y=1发生的概率”，按理来说应在0~1之间，但会出现预测值 y_hat < 0 或 > 1 的不现实情况

所以需要通过一个连接函数把取值限定在 0~1 之间：

 为什么可以把 y_hat 理解为 “y=1发生的概率”：在两点分布模型的基础上，

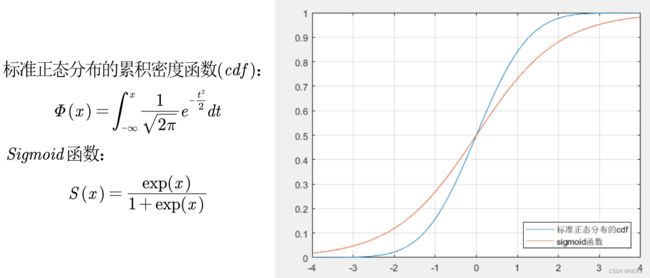
连接函数的取法（两种回归）：

① 标准正态分布累计密度函数的probit回归 ② Sigmoid函数的逻辑回归

由于后者有解析表达式（而标准正态分布的 cdf 没有），所以计算 logistic 模型比probit模型更为方便

（红框内容放入论文）

f1=@(x) normcdf(x); % 标准正态分布的累积分布函数
fplot(f1, [-4,4]); % 在-4到
4上画出匿名函数的图形
hold on;
grid on;
f2=@(x) exp(x)/(1+exp(x));
fplot(f2, [-4,4]);
legend('标准正态分布的cdf','sigmoid函数','location','SouthEast')

怎么求解添加连接函数后的模型（即求出系数 βi ）：没有写全

求出模型中未知数 β 后怎么预测待分类样本属于哪一个类：

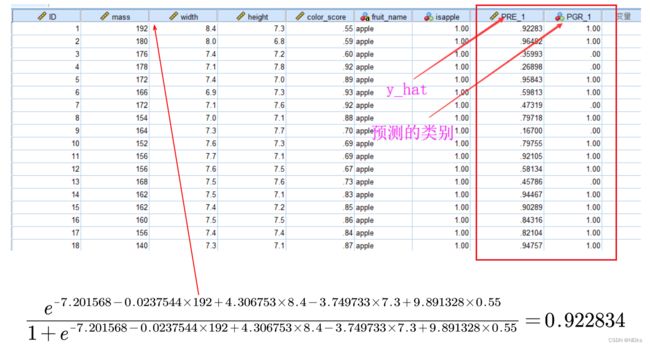
将待测样本的 xi 已知数据代入模型中，求出 y_hat，y_hat >= 0.5就认为 y=1，该样本属于y=1对应的分类（原理：把 y_hat 理解为 y = 1 发生的概率）

（红框内容放入论文）

Spss求解逻辑回归

步骤

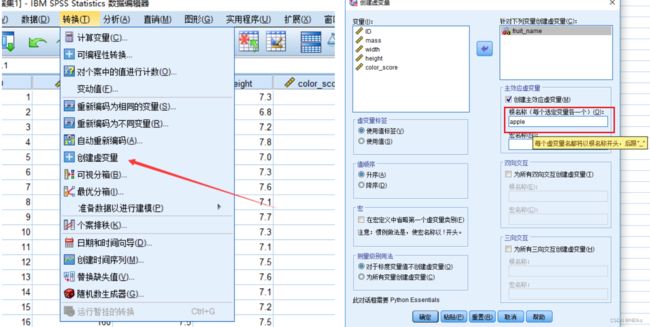
先把因变量（分类的类别）转化为分类变量（虚拟变量）：

SPSS创建虚拟变量：工具栏的 转换 - 创建虚变量 - 输入根名称

在底部“变量视图”中可查看变量、修改变量名等 

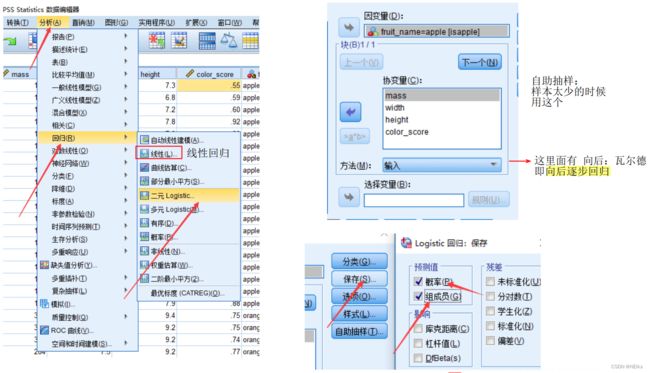
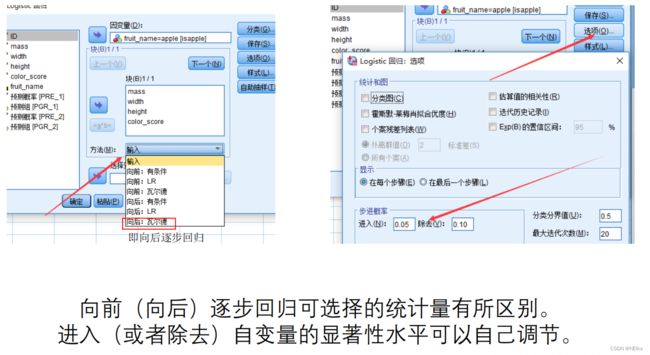
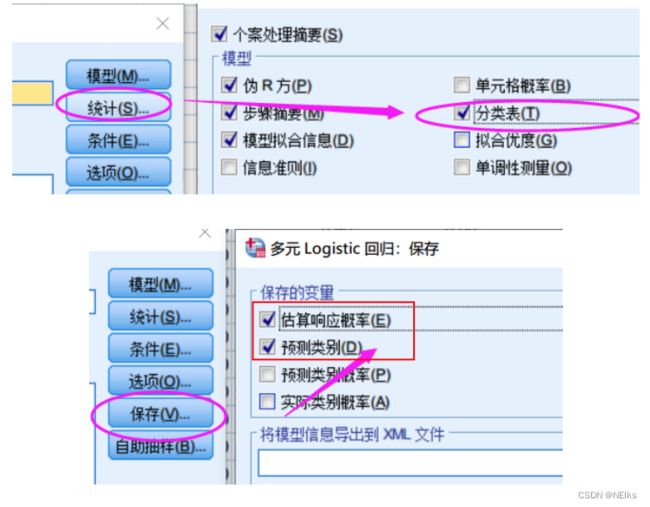
SPSS逻辑回归：分析 - 回归 - 二元logistic；添加协变量、自变量；若有分类变量就要点 分类 - 分类协变量 来创建虚拟变量；在 保存 中，勾选上预测值组中的 概率、组成员；选项 中可以选择进行逐步回归；样本数目太少就可以点击 自助抽样

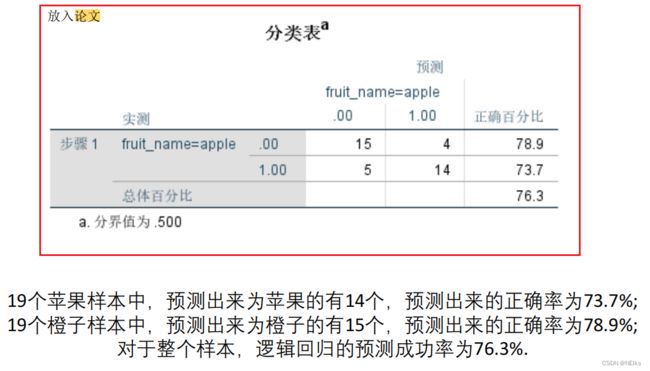
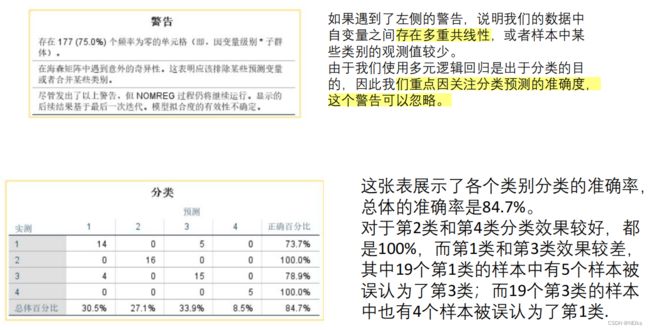
查看结果表：分类表、逻辑回归系数表放入论文

逐步回归的设置

自变量有分类变量

添加到分类协变量

预测结果差：添加平方项/交互项

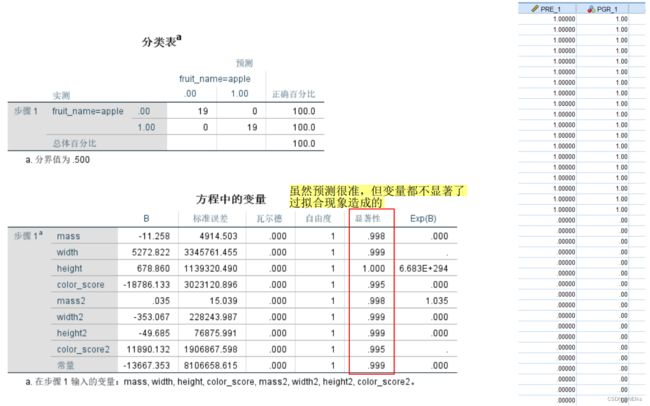
添加新的平方项的列（这里例子的所有自变量都加了一个平方项）：

过拟合现象

如何确定合适的模型：交叉验证

假如现在有了模型1和加了平方项的模型2，要测哪个更准：

       把数据分为训练组、测试组，用训练组的数据来估计模型，测试组的数据来验证模型的预测结果
       从原始数据中随机抽出几个作为测试组
       看哪个模型预测的更准
       为了消除偶然性的影响，可以多随机抽取测试组 多做几次训练与测试，最终对每个模型求平均准确率，该步骤为交叉验证

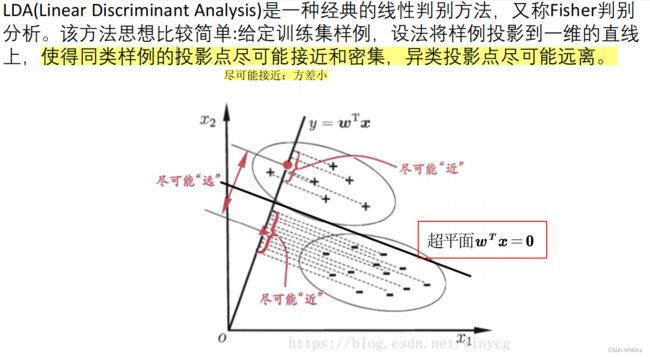
Fisher线性判别分析

思想：找个超平面，把不同种类的点分开，同类样例的投影点尽可能接近和密集，异类投影点尽可能远离

原理：机器学习-线性分类3-线性判别分析（Fisher判别分析）-模型定义_哔哩哔哩_bilibili

核心问题：找到线性系数向量 ω

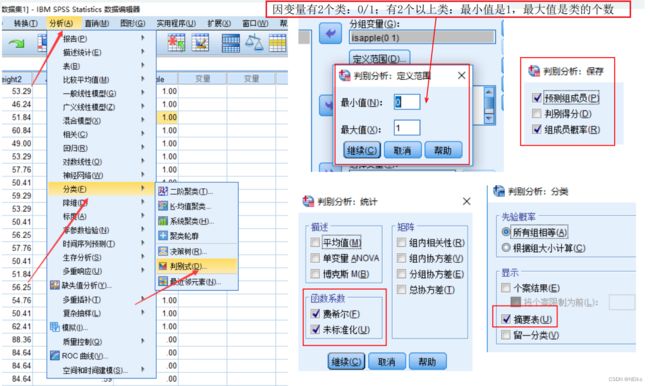
SPSS操作

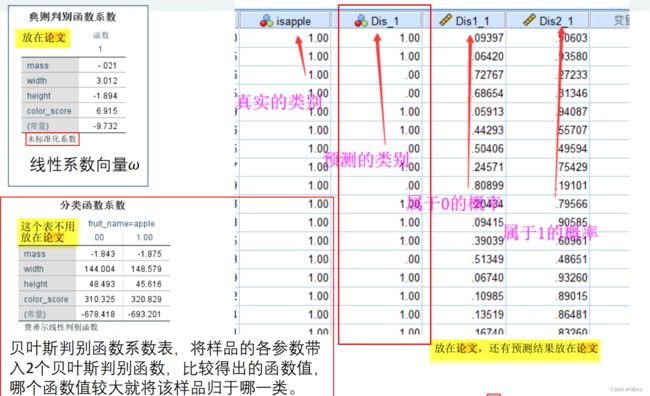
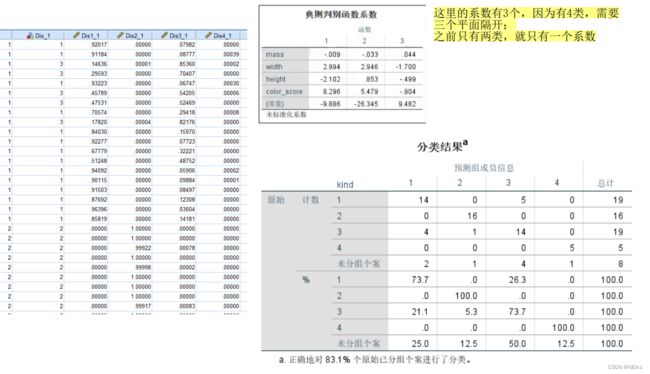
结果：

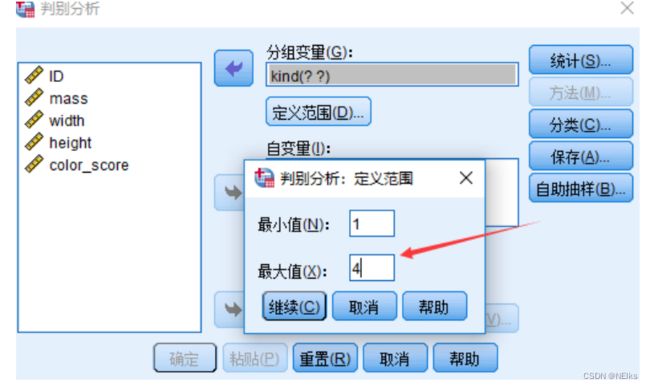
多分类问题

生成因变量的分类序号：在excel中 - 替换

Fisher判别分析

https://blog.csdn.net/z962013489/article/details/79918758

调整因变量的范围即可：

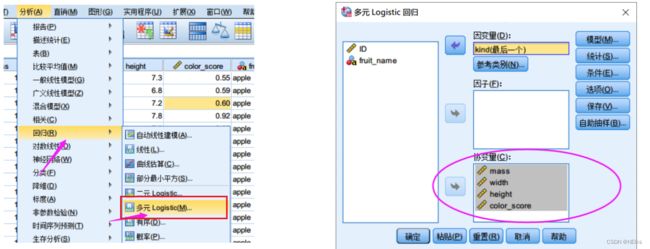
Logistic回归

https://www.cnblogs.com/bonelee/p/8127411.html

https://blog.csdn.net/bitcarmanlee/article/details/82440853

 

Spss中因子和协变量的区别

因子：指分类型变量，例如性别、学历等

协变量：指连续型变量，例如面积、重量等