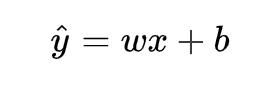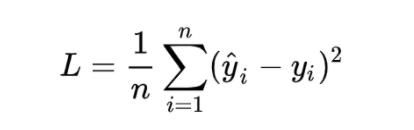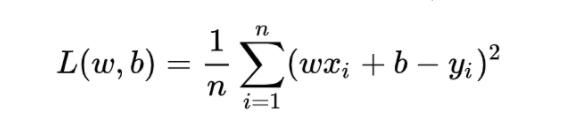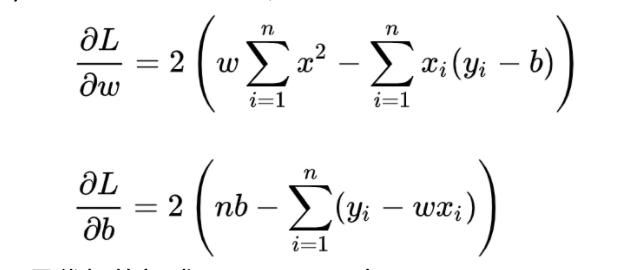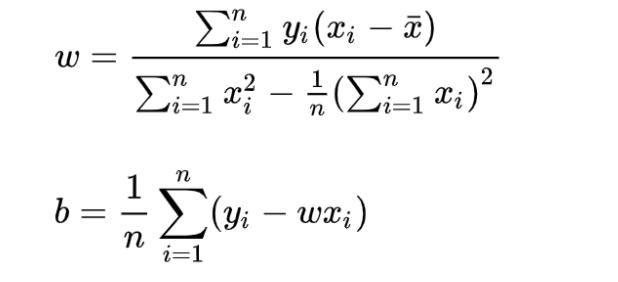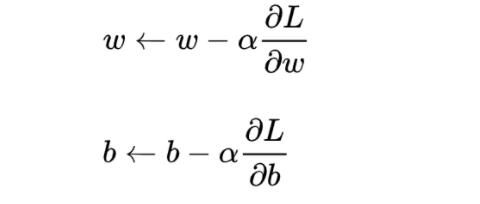pytorch线性回归代码_机器学习｜算法笔记（二）线性回归算法以及代码实现

概述

上一篇讲述了《机器学习｜算法笔记(一)k近邻(KNN)算法以及应用实现》，本篇讲述机器学习算法线性回归，内容包括模型介绍及代码实现。

线性回归

线性回归是回归问题中的一种，线性回归假设目标值与特征之间线性相关，即满足一个多元一次方程。通过构建损失函数，来求解损失函数最小时的参数w和b。通长我们可以表达成如下公式：

y^为预测值，自变量x和因变量y是已知的，而我们想实现的是预测新增一个x，其对应的y是多少。因此，为了构建这个函数关系，目标是通过已知数据点，求解线性模型中w和b两个参数。

目标/损失函数

求解最佳参数，需要一个标准来对结果进行衡量，为此我们需要定量化一个目标函数式，使得计算机可以在求解过程中不断地优化。

针对任何模型求解问题，都是最终都是可以得到一组预测值y^ ，对比已有的真实值 y ，数据行数为 n ，可以将损失函数定义如下：

即预测值与真实值之间的平均的平方距离，统计中一般称其为MAE(mean square error)均方误差。把之前的函数式代入损失函数，并且将需要求解的参数w和b看做是函数L的自变量，可得

现在的任务是求解最小化L时w和b的值，

即核心目标优化式为

求解方法

1)最小二乘法(least square method)

求解 w 和 b 是使损失函数最小化的过程，在统计中，称为线性回归模型的最小二乘“参数估计”(parameter estimation)。我们可以将 L(w,b) 分别对 w 和 b 求导，得到

令上述两式为0，可得到 w 和 b 最优解的闭式(closed-form)解：

2)梯度下降(gradient descent)

梯度下降核心内容是对自变量进行不断的更新(针对w和b求偏导)，使得目标函数不断逼近最小值的过程

代码实现

liner_regression.py

# -*- coding: utf-8 -*-import numpy as npclass LinerRegression(object):    def __init__(self, learning_rate=0.01, max_iter=100, seed=None):        np.random.seed(seed)        self.lr = learning_rate        self.max_iter = max_iter        self.w = np.random.normal(1, 0.1)        self.b = np.random.normal(1, 0.1)        self.loss_arr = []    def fit(self, x, y):        self.x = x        self.y = y        for i in range(self.max_iter):            self._train_step()            self.loss_arr.append(self.loss())            # print('loss: {:.3}'.format(self.loss()))            # print('w: {:.3}'.format(self.w))            # print('b: {:.3}'.format(self.b))    def _f(self, x, w, b):        return x * w + b    def predict(self, x=None):        if x is None:            x = self.x        y_pred = self._f(x, self.w, self.b)        return y_pred    def loss(self, y_true=None, y_pred=None):        if y_true is None or y_pred is None:            y_true = self.y            y_pred = self.predict(self.x)        return np.mean((y_true - y_pred)**2)    def _calc_gradient(self):        d_w = np.mean((self.x * self.w + self.b - self.y) * self.x)        d_b = np.mean(self.x * self.w + self.b - self.y)        return d_w, d_b    def _train_step(self):        d_w, d_b = self._calc_gradient()        self.w = self.w - self.lr * d_w        self.b = self.b - self.lr * d_b        return self.w, self.b

train.py

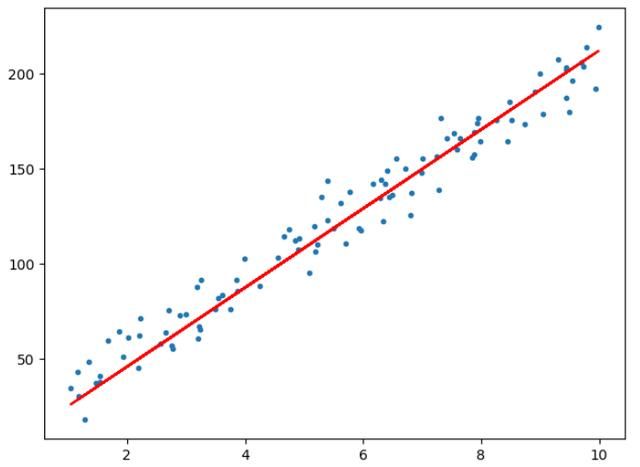
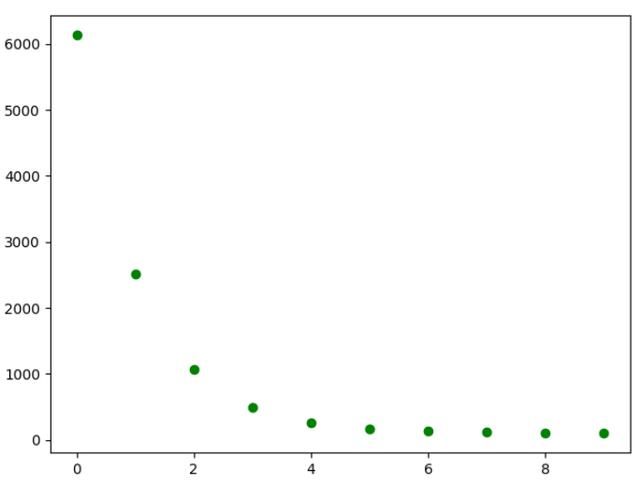
# -*- coding: utf-8 -*-import numpy as npimport matplotlib.pyplot as pltfrom liner_regression import *def show_data(x, y, w=None, b=None):    plt.scatter(x, y, marker='.')    if w is not None and b is not None:        plt.plot(x, w*x+b, c='red')    plt.show()# data generationnp.random.seed(272)data_size = 100x = np.random.uniform(low=1.0, high=10.0, size=data_size)y = x * 20 + 10 + np.random.normal(loc=0.0, scale=10.0, size=data_size)# plt.scatter(x, y, marker='.')# plt.show()# train / test splitshuffled_index = np.random.permutation(data_size)x = x[shuffled_index]y = y[shuffled_index]split_index = int(data_size * 0.7)x_train = x[:split_index]y_train = y[:split_index]x_test = x[split_index:]y_test = y[split_index:]# visualize data# plt.scatter(x_train, y_train, marker='.')# plt.show()# plt.scatter(x_test, y_test, marker='.')# plt.show()# train the liner regression modelregr = LinerRegression(learning_rate=0.01, max_iter=10, seed=314)regr.fit(x_train, y_train)print('cost: {:.3}'.format(regr.loss()))print('w: {:.3}'.format(regr.w))print('b: {:.3}'.format(regr.b))show_data(x, y, regr.w, regr.b)# plot the evolution of costplt.scatter(np.arange(len(regr.loss_arr)), regr.loss_arr, marker='o', c='green')plt.show()

运行结果展示

总结

上述代码实现首先建立liner_regression.py文件，用于实现线性回归的类文件，包含了线性回归内部的核心函数，建立 train.py 文件，用于生成模拟数据，并调用 liner_regression.py 中的类，完成线性回归任务，最后给出了线性回归后的效果图，下一篇讲述机器学习算法支持向量机(SVM)，欢迎关注。