求强连通分量的Tarjan算法
求强连通分量的Tarjan算法
[有向图强连通分量]
在有向图G中,如果两个顶点间至少存在一条路径,称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。非强连通图有向图的极大强连通子图,称为强连通分量(strongly connected components)。
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
直接根据定义,用双向遍历取交集的方法求强连通分量,时间复杂度为O(N^2+M)。更好的方法是Kosaraju算法或Tarjan算法,两者的时间复杂度都是O(N+M)。本文介绍的是Tarjan算法。
[Tarjan算法]
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。由定义可以得出,
Low(u)=Min { DFN(u), Low(v),(u,v)为树枝边,u为v的父节点 DFN(v),(u,v)为指向栈中节点的后向边(非横叉边) } |
当DFN(u)=Low(u)时,以u为根的搜索子树上所有节点是一个强连通分量。
算法伪代码如下
tarjan(u) { DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值 Stack.push(u) // 将节点u压入栈中 for each (u, v) in E // 枚举每一条边 if (v is not visted) // 如果节点v未被访问过 tarjan(v) // 继续向下找 Low[u] = min(Low[u], Low[v]) else if (v in S) // 如果节点v还在栈内 Low[u] = min(Low[u], DFN[v]) if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根 repeat v = S.pop // 将v退栈,为该强连通分量中一个顶点 print v until (u== v) } |
接下来是对算法流程的演示。
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。
继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
至此,算法结束。经过该算法,求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
可以发现,运行Tarjan算法的过程中,每个顶点都被访问了一次,且只进出了一次堆栈,每条边也只被访问了一次,所以该算法的时间复杂度为O(N+M)。
求有向图的强连通分量还有一个强有力的算法,为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法,其时间复杂度也是O(N+M)。与Trajan算法相比,Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS,不用建立逆图,更简洁。在实际的测试中,Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外,该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法,也有助于深入理解求双连通分量的Tarjan算法,两者可以类比、组合理解。
求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法,以及求最近公共祖先的离线Tarjan算法,在此对Tarjan表示崇高的敬意。
附:tarjan算法的C++程序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
void tarjan(int i) { int j; DFN[i]=LOW[i]=++Dindex; instack[i]=true; Stap[++Stop]=i; for (edge *e=V[i];e;e=e->next) { j=e->t; if (!DFN[j]) { tarjan(j); if (LOW[j]<LOW[i]) LOW[i]=LOW[j]; } else if (instack[j] && DFN[j]<LOW[i]) LOW[i]=DFN[j]; } if (DFN[i]==LOW[i]) { Bcnt++; do { j=Stap[Stop--]; instack[j]=false; Belong[j]=Bcnt; } while (j!=i); } } void solve() { int i; Stop=Bcnt=Dindex=0; memset(DFN,0,sizeof(DFN)); for (i=1;i<=N;i++) if (!DFN[i]) tarjan(i); } |
[参考资料]
BYVoid 原创作品,转载请注明。
说到以Tarjan命名的算法,我们经常提到的有3个,其中就包括本文所介绍的求强连通分量的Tarjan算法。而提出此算法的普林斯顿大学的Robert E Tarjan教授也是1986年的图灵奖获得者(具体原因请看本博“历届图灵奖得主”一文)。
首先明确几个概念。
- 强连通图。在一个强连通图中,任意两个点都通过一定路径互相连通。比如图一是一个强连通图,而图二不是。因为没有一条路使得点4到达点1、2或3。

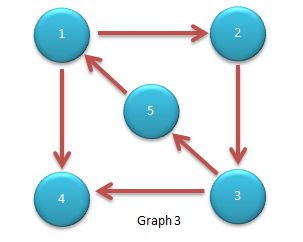
- 强连通分量。在一个非强连通图中极大的强连通子图就是该图的强连通分量。比如图三中子图{1,2,3,5}是一个强连通分量,子图{4}是一个强连通分量。
关于Tarjan算法的伪代码和流程演示请到我的115网盘下载网上某大牛写的Doc(地址:http://u.115.com/file/f96af404d2<Tarjan算法.doc>)本文着重从另外一个角度,也就是针对tarjan的操作规则来讲解这个算法。
其实,tarjan算法的基础是DFS。我们准备两个数组Low和Dfn。Low数组是一个标记数组,记录该点所在的强连通子图所在搜索子树的根节点的Dfn值(很绕嘴,往下看你就会明白),Dfn数组记录搜索到该点的时间,也就是第几个搜索这个点的。根据以下几条规则,经过搜索遍历该图(无需回溯)和对栈的操作,我们就可以得到该有向图的强连通分量。
- 数组的初始化:当首次搜索到点p时,Dfn与Low数组的值都为到该点的时间。
- 堆栈:每搜索到一个点,将它压入栈顶。
- 当点p有与点p’相连时,如果此时(时间为dfn[p]时)p’不在栈中,p的low值为两点的low值中较小的一个。
- 当点p有与点p’相连时,如果此时(时间为dfn[p]时)p’在栈中,p的low值为p的low值和p’的dfn值中较小的一个。
- 每当搜索到一个点经过以上操作后(也就是子树已经全部遍历)的low值等于dfn值,则将它以及在它之上的元素弹出栈。这些出栈的元素组成一个强连通分量。
- 继续搜索(或许会更换搜索的起点,因为整个有向图可能分为两个不连通的部分),直到所有点被遍历。
由于每个顶点只访问过一次,每条边也只访问过一次,我们就可以在O(n+m)的时间内求出有向图的强连通分量。但是,这么做的原因是什么呢?
Tarjan算法的操作原理如下:
- Tarjan算法基于定理:在任何深度优先搜索中,同一强连通分量内的所有顶点均在同一棵深度优先搜索树中。也就是说,强连通分量一定是有向图的某个深搜树子树。
- 可以证明,当一个点既是强连通子图Ⅰ中的点,又是强连通子图Ⅱ中的点,则它是强连通子图Ⅰ∪Ⅱ中的点。
- 这样,我们用low值记录该点所在强连通子图对应的搜索子树的根节点的Dfn值。注意,该子树中的元素在栈中一定是相邻的,且根节点在栈中一定位于所有子树元素的最下方。
- 强连通分量是由若干个环组成的。所以,当有环形成时(也就是搜索的下一个点已在栈中),我们将这一条路径的low值统一,即这条路径上的点属于同一个强连通分量。
- 如果遍历完整个搜索树后某个点的dfn值等于low值,则它是该搜索子树的根。这时,它以上(包括它自己)一直到栈顶的所有元素组成一个强连通分量。
参考代码:
1 program tarjan; 2 var 3 v,f:array[1..100]of boolean; 4 dfn,low:array[1..100]of integer; 5 a:array[0..100,0..100]of integer; //边表 6 i,j,n,m,x,y,deep,d:integer; 7 stack,ln:array[1..100]of integer; 8 function min(x,y:longint):integer; 9 begin 10 if x>y then exit(y) 11 else exit(x); 12 end; 13 procedure print(x:integer); //出栈,打印 14 begin 15 while stack[deep]<>x do 16 begin 17 write(stack[deep],' '); 18 f[stack[deep]]:=false; 19 dec(deep); 20 end; 21 writeln(stack[deep]); 22 f[stack[deep]]:=false; //去除入栈标记 23 dec(deep); 24 end; 25 procedure dfs(x:integer); 26 var 27 i:integer; 28 begin 29 inc(d); //时间 30 dfn[x]:=d; //规则1 31 low[x]:=d; 32 inc(deep); //栈中元素个数 33 stack[deep]:=x; //规则2 34 f[x]:=true; 35 for i:=1 to a[x,0] do 36 if not v[a[x,i]] then 37 begin 38 v[a[x,i]]:=true; 39 dfs(a[x,i]); 40 low[x]:=min(low[a[x,i]],low[x]); //规则3 41 end 42 else if f[a[x,i]] then 43 low[x]:=min(low[x],dfn[a[x,i]]); //规则4 44 if dfn[x]=low[x] then //规则5 45 print(x); 46 end; 47 begin 48 readln(n,m); 49 fillchar(a,sizeof(a),0); 50 for i:=1 to m do 51 begin 52 readln(x,y); //读入图 53 inc(a[x,0]); 54 a[x,a[x,0]]:=y; 55 end; 56 for i:=1 to n do 57 if not v[i] then 58 begin 59 v[i]:=true; 60 dfs(i); //更换起点,规则6 61 end; 62 end.
本文地址:http://www.cnblogs.com/saltless/archive/2010/11/08/1871430.html
(saltless原创,转载请注明出处)
百度百科:
vector之所以被认为是一个容器,是因为它能够像容器一样存放各种类型的对象,简单地说,vector是一个能够存放任意类型的动态数组,能够增加和压缩数据。
为了可以使用vector,必须在你的头文件中包含下面的代码:
#include <vector>
vector属于std命名域的,因此需要通过命名限定,如下完成你的代码:
using std::vector;
vector<int> vInts;
或者连在一起,使用全名:
std::vector<int> vInts;
建议在代码量不大,并且使用的命名空间不多的情况下,使用全局的命名域方式:using namespace std;
函数
表述
c.assign(beg,end) c.assign(n,elem)
将(beg; end)区间中的数据赋值给c。将n个elem的拷贝赋值给c。
c.at(idx)
传回索引idx所指的数据,如果idx越界,抛出out_of_range。
c.back()
传回最后一个数据,不检查这个数据是否存在。
c.begin()
传回迭代器中的第一个数据地址。
c.capacity()
返回容器中数据个数。
c.clear()
移除容器中所有数据。
c.empty()
判断容器是否为空。
c.end() //指向迭代器中末端元素的下一个,指向一个不存在元素。
c.erase(pos)// 删除pos位置的数据,传回下一个数据的位置。
c.erase(beg,end)
删除[beg,end)区间的数据,传回下一个数据的位置。
c.front()
传回第一个数据。
get_allocator
使用构造函数返回一个拷贝。
c.insert(pos,elem)//在pos位置插入一个elem拷贝,传回新数据位置
c.insert(pos,n,elem)//在pos位置插入n个elem数据,无返回值
c.insert(pos,beg,end)//在pos位置插入在[beg,end)区间的数据。无返回值
c.max_size()
返回容器中最大数据的数量。
c.pop_back()
删除最后一个数据。
c.push_back(elem)
在尾部加入一个数据。
c.rbegin()
传回一个逆向队列的第一个数据。
c.rend()
传回一个逆向队列的最后一个数据的下一个位置。
c.resize(num)
重新指定队列的长度。
c.reserve()
保留适当的容量。
c.size()
返回容器中实际数据的个数。
c1.swap(c2)//将c1和c2元素互换
swap(c1,c2)//同上操作。
vector<Elem> //创建一个空的vector
vector<Elem> c1(c2)//复制一个vector
vector <Elem> c(n)//创建一个vector,含有n个数据,数据均已缺省构造产生
vector <Elem> c(n,elem)//创建一个含有n个elem拷贝的vector
vector <Elem> c(beg,end)//创建一个以(beg;end)为区间的vector
c.~ vector <Elem>()//销毁所有数据,释放内存
operator[]
返回容器中指定位置的一个引用。
创建一个vector
vector容器提供了多种创建方法,下面介绍几种常用的。
创建一个Widget类型的空的vector对象:
vector<Widget> vWidgets;
创建一个包含500个Widget类型数据的vector:
vector<Widget> vWidgets(500);
创建一个包含500个Widget类型数据的vector,并且都初始化为0:
vector<Widget> vWidgets(500,Widget(0));
创建一个Widget的拷贝:
vector<Widget> vWidgetsFromAnother(vWidgets);
向vector添加一个数据
vector添加数据的缺省方法是push_back()。push_back()函数表示将数据添加到vector的尾部,并按需要来分配内存。例如:向vector<Widget>;中添加10个数据,需要如下编写代码: for(int i= 0;i<10; i++) { vWidgets.push_back(Widget(i)); }
获取vector中指定位置的数据
vector里面的数据是动态分配的,使用push_back()的一系列分配空间常常决定于文件或一些数据源。如果想知道vector是否为空,可以使用empty(),空返回true,否则返回false。获取vector的大小,可以使用size()。例如,如果想获取一个vector v的大小,但不知道它是否为空,或者已经包含了数据,如果为空时想设置为 -1,你可以使用下面的代码实现:
int nSize = v.empty() -1 : static_cast<int>(v.size());
访问vector中的数据
使用两种方法来访问vector。
1、 vector::at()
2、 vector::operator[]
operator[]主要是为了与C语言进行兼容。它可以像C语言数组一样操作。但at()是我们的首选,因为at()进行了边界检查,如果访问超过了vector的范围,将抛出一个例外。由于operator[]容易造成一些错误,所有我们很少用它,下面进行验证一下:
分析下面的代码:
vector<int> v;
v.reserve(10);
for(int i=0; i<7; i++) {
v.push_back(i); //在V的尾部加入7个数据
}
try {int iVal1 = v[7];
// not bounds checked - will not throw
int iVal2 = v.at(7);
// bounds checked - will throw if out of range
}
catch(const exception& e) {
cout << e.what();
}
删除vector中的数据
vector能够非常容易地添加数据,也能很方便地取出数据,同样vector提供了erase(),pop_back(),clear()来删除数据,当删除数据时,应该知道要删除尾部的数据,或者是删除所有数据,还是个别的数据。
remove()算法 如果要使用remove,需要在头文件中包含如下代码:
#include <algorithm>
remove有三个参数:
1、 iterator _First:指向第一个数据的迭代指针。
2、 iterator _Last:指向最后一个数据的迭代指针。
3、 predicate _Pred:一个可以对迭代操作的条件函数。