数据结构---克鲁斯卡尔(Kruskal)算法
数据结构(C语言)---克鲁斯卡尔(Kruskal)算法
-
- 一、总体思路
- 二、代码实现步骤
-
- 0.结构
- 1.构建边集数组
- 2.权值排序
- 3.生成最小生成树
- 三、完整代码
- 四、图解
一、总体思路
总体思路:以边构建
直接找最小权值的边来构建生成树,注意考虑环路的形成
二、代码实现步骤
0.结构
主要两部分
①图:由邻接矩阵构成,包括图的顶点数、边数;
②边集表:包括起点、终点、边数的权值。

#define INFINITY 65535
#define MAXVEX 20
#define MAXEDGE 20
typedef struct
{
int arc[MAXVEX][MAXVEX];//邻接矩阵
int numVertexes, numEdges;//顶点数、边数
}MGraph;//图
typedef struct
{
int begin;
int end;
int weight;
}Edge;//边集数组结构
1.构建边集数组
①用邻接矩阵创建图
void CreateMGraph(MGraph* G)
{
int i, j;
G->numEdges = 15;
G->numVertexes = 9;
//初始化邻接矩阵
for (i = 0; i < G->numVertexes; i++)
{
for (j = 0; j < G->numVertexes; j++)
{
if (i == j)
G->arc[i][j] = 0;
else
G->arc[i][j] = G->arc[j][i] = INFINITY;
}
}
G->arc[0][1] = 10;
G->arc[0][5] = 11;
G->arc[1][2] = 18;
G->arc[1][8] = 12;
G->arc[1][6] = 16;
G->arc[2][8] = 8;
G->arc[2][3] = 22;
G->arc[3][8] = 21;
G->arc[3][6] = 24;
G->arc[3][7] = 16;
G->arc[3][4] = 20;
G->arc[4][7] = 7;
G->arc[4][5] = 26;
G->arc[5][6] = 17;
G->arc[6][7] = 19;
for (i = 0; i < G->numVertexes; i++)
{
for (j = i; j < G->numVertexes; j++)
{
G->arc[j][i] = G->arc[i][j];
}
}
}
②构建边集数组
int i, j;
int k = 0;
int parent[MAXVEX];//判断是否形成环的数组
Edge edges[MAXEDGE];//边集数组,edge的结构为begin,end,weight,均为整型
//构建边集数组
//将邻接矩阵转换为边集数组
for (i = 0; i < G.numVertexes - 1; i++)
{
for (j = i + 1; j < G.numVertexes ; j++)
{
if (G.arc[i][j] < INFINITY)
{
edges[k].begin = i;
edges[k].end = j;
edges[k].weight = G.arc[i][j];
k++;
}
}
}
2.权值排序
//交换头尾、权值
void Swap(Edge* edges, int i, int j)
{
int t;
t = edges[i].begin;
edges[i].begin = edges[j].begin;
edges[j].begin = t;
t = edges[i].weight;
edges[i].weight = edges[j].weight;
edges[j].weight = t;
t = edges[i].end;
edges[i].end = edges[j].end;
edges[j].end = t;
}
//权值排序
void Sort(Edge edges[], MGraph* G)
{
int i, j;
for (i = 0; i < G->numEdges; i++)
{
for (j = i+1; j < G->numEdges; j++)//选择排序
{
if (edges[i].weight > edges[j].weight)
{
Swap(edges, i, j);
}
}
}
printf("权排序之后的为:\n");
for (i = 0; i < G->numEdges; i++)
{
printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
}
}
3.生成最小生成树
//非常关键
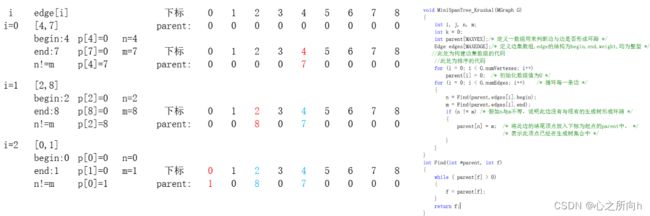
int Find(int* parent, int f)
{
while (parent[f] > 0)//已加入生成树集合
{
f = parent[f];//找到与它连通的最大顶点
}
//若该点没有加入生成树集合,就返回该点本身
return f;
}
void MiniSpanTree_Kruskal(MGraph G)
{
int i, j,n,m;
int k = 0;
int parent[MAXVEX];//判断是否形成环的数组
Edge edges[MAXEDGE];//边集数组,edge的结构为begin,end,weight,均为整型
//构建边集数组的代码
//排序
Sort(edges, &G);
/* ************* 算法关键 ****************** */
for (i = 0; i < G.numVertexes; i++)
parent[i] = 0;//初始化数组
printf("打印最小生成树:\n");
for (i = 0; i < G.numEdges; i++)/* 循环每一条边 */
{
n = Find(parent, edges[i].begin);//从起点开始找
m = Find(parent, edges[i].end);//从终点开始找
if (n != m)//没有形成环
{
parent[n] = m;//将此边的结尾顶点 放入 下标为起点的parent中,
//表示该顶点已在生成树集合中
printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
}
}
}
三、完整代码
#include