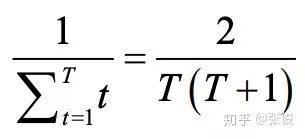树的高度从零还是一开始数_Science论文解读:打牌一时爽,一直打牌一直爽
作者丨王曲苑
学校丨西南大学博士生
研究方向丨人工智能、边缘计算
近些年来,AI 取得长足进步的同时,游戏一直伴随其左右,不论是Dota、星际、围棋还是德州扑克都成为检验其发展程度的验金石。2005 年 Michael Bowling 等人就在《Science》上发表《Heads-up limit hold’em poker is solved》,2018 年 Noam Brown 等人在《Science》发表《Superhuman AI for heads-up no-limit poker: Libratus beats top professionals》的论文研讨如何用 AI 打德扑 [1-2]。
但是在以往工作中往往聚焦于只有两位玩家的牌局,这在现实牌局中往往是不现实的,于是 Noam Brown 等人继续研究如何用 AI 应对德扑多人牌局,其成果题为《Superhuman AI for multiplayer poker》发表于《Science》[3],本文即对这篇论文进行简要分析与解读。
论文链接:https://www.paperweekly.site/papers/3233
引言
扑克能作为 AI 和博弈论领域挑战问题的原因很简单:没有别的休闲游戏能像扑克一样要求人们优雅且高效地捕捉隐藏信息。虽然扑克仅仅被看为衡量 AI 和博弈论发展的验金石,但是策略设置中隐藏信息带来的挑战绝不仅局限于这些休闲游戏中。
但是过去的 20 年间,所有利用 AI 打扑克的系统都只设置了 2 名玩家。设计一种针对多人牌局的超人类 AI 被普遍看做是 AI 发展的下一个关键节点。作者在这篇文章中描述了 Pluribus,一种能够在 6 人牌局中打败顶尖人类选手的新型 AI 系统。值得注意的是,这个系统是 18 年提出的 Libratus 系统的改进升级版。
多人博弈中的理论和实际挑战
正如前文所说,目前 AI 在游戏领域取得的成绩基均是基于双人零和博弈模型,简单来说就是两人或两队“你赢我输,我输你赢”的模式。由于模型特性和纳什均衡性质,我们可以证明:在双人零和博弈模型中,倘若应用纳什均衡策略则至少可以保证不输,换言之,在双人零和博弈模型中应用纳什均衡策略是不可击败的(例如两人进行石头剪刀布游戏的纳什均衡就是等概率出石头剪刀布)。这也是之前那些 AI 算法取得成功的原因:不遗余力寻找纳什均衡。
但是面对更复杂的问题,纳什均衡就心有余而力不足了。目前还没有一种能在多项式时间内找到双人非零和博弈纳什均衡的算法。就算是零和博弈,想找到 3 人或更多玩家零和博弈的纳什均衡也是十分困难的。
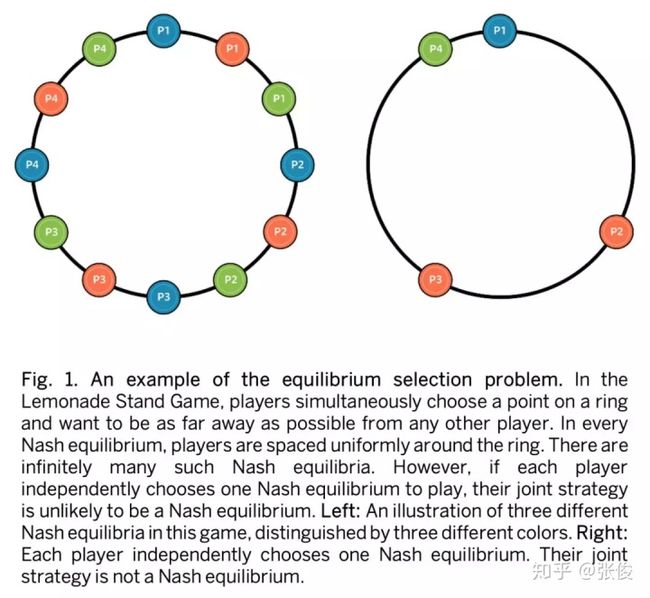
即使在多人博弈中每个玩家都得到了纳什均衡策略,这样执行下来的结果未必是纳什均衡的,Lemonade stand game 就是一个典型例子[4]。在 Lemonade stand game 中多个玩家同时在一个圆环上选择位置,目标是距离别人越远越好。这个博弈的纳什均衡是每个玩家在圆环上均匀分布,能达到这样效果的策略有无数多种,倘若每个玩家独立计算一种,则产生的联合策略不一定是纳什均衡,如图 1 所示。
纳什均衡的短板引发了众多科学家的思考:面对此类博弈问题,我们该如何解决。因此,作者认为在 6 人牌局中,我们的目标不应该是去寻找某一种特定的博弈理论求解,而是创建一个能够以经验为主的可以持续击败人类的 AI 系统。
因此作者提出了 Pluribus 系统,尽管在理论上作者无法保证最后的策略一定是纳什均衡的,但是通过观察实验发现,所设计的 AI 系统能够稳定地以某种强策略击败顶级人类玩家。虽然这样的技术没有足够的理论支撑,但是仍然都够在更为广阔的领域产生更多超人策略。
Pluribus描述
Pluribus 策略核心是持续不断地进行自学习自博弈,也就是说在这样的训练方式中,AI 系统之和自己的镜像进行对抗,而不获取任何人类游戏数据或先前的 AI 游戏数据。起初,AI 随机选择玩法,然后逐步改变其行动并确定行动的概率分布,最终,AI 的表现会取得明显提升。
作者称 Pluribus 利用自学习制定的离线策略为“蓝图策略”,随着真实游戏的进行,Pluribus 通过在比赛中自己的实际情况实时搜索更好的策略来改进蓝图策略。
大规模不完全信息博弈抽象
无限制的德州扑克中有太多的决策点可以单独推理。为了降低游戏的复杂性,作者消除了一些考虑因素并且将类似的决策点放在一起,这个过程称之为抽象。在抽象之后,划分的决策点被视为相同决策。作者在 Pluribus 中使用了两种抽象:动作抽象和信息抽象。
动作抽象减少了 AI 所需要考虑的动作数。在无限制的德扑中,通常允许玩家在 100 刀至 10000 刀之间进行任意价格投注。但是,在现实情况中投注 200 刀和 201 刀几乎没有区别。
为了降低形成策略的复杂性,Pluribus 在任何给定的决策点只考虑几种不同的下注大小。它所考虑的确切投注数量在 1 到 14 之间变化,具体取决于具体情况。但是对手并不局限于那些少数选项。如果对手下注 150 美元而 Pluribus 只接受过 100 美元或 200 美元的投注训练,会发生什么?一般来说,Pluribus 会依赖于搜索算法实时对这种“离树”行为产生相应。
信息抽象对于所揭示信息(如玩家的牌和显示的牌)类似的决策点进行合并。举例来说 10-high str AI ght 和 9-high str AI ght 在牌型上差距明显,但是策略层面却是相似的。Pluribus 可以将这些牌型放在一起并对其进行相同的处理,从而减少了确定策略所需的不同情况的数量。信息抽象大大降低了游戏的复杂性,但它可能会消除一些对于超人表现来说非常重要的微妙差异。因此,在与人类的实际比赛中,Pluribus 仅使用信息抽象来推断未来下注轮次的情况,而不是实际所在的下注轮次。
通过改进型蒙特卡洛CFR来进行自学习训练
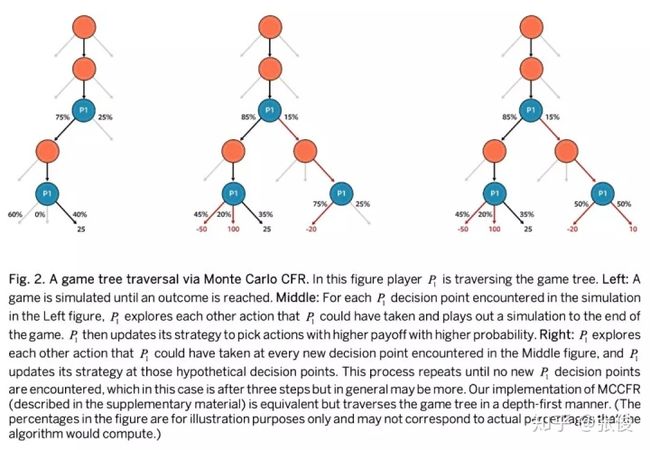
Pluribus 所使用的蓝图策略是 CFR(counterfactual regret minimization)中的一种。CFR 是一种迭自学习训练算法, AI 从完全随机开始,通过学习击败其早期版本逐渐改进。过去 6 年间几乎所有德扑 AI 都采用了 CFR 变形中的一种。在本文中,作者采用一种蒙特卡洛 CFR(Monte Carlo CFR) 方法对博弈树上的行动进行采样而不是在每次迭代时遍历博弈树。
在每次算法迭代中,MCCFR 指定一名玩家为遍历者(traverser),他的当前策略将在迭代时更新。迭代开始时,MCCFR 会根据所有玩家的当前策略模拟一手牌。一旦模拟结束,AI 就会审查遍历者做出的每个决定,并考虑如果采用其他可行行动会更好还是更差。接下来,AI 会考虑在其他可行行动之后可能做出的每个假设决策,考虑其行动更好还是更差,以此往复。博弈树如图 2 所示。
在本文中,探索其他假设结果是可能的,因为 AI 知道每个玩家的迭代策略,因此可以模拟在选择其他行动时会发生什么。这种反事实推理是将 CFR 与其他自学习训练算法(Alphago、Dota2、星际争霸 2 等使用的)区分开来的重要特点之一。
遍历者选择某种行为应获得的和实际所得的差值被添加到此次行动的后悔值中(counterfactual regret),这代表了在之前迭代中遍历者没有选择该行动的后悔值,迭代结束时,更新遍历者的策略使得其以更高概率选择具有更高后悔值的行动。尽管 CFR 方法没法保证双人零和博弈模型之外的策略达到纳什均衡,但是他可以在所有有限博弈中保证后悔值在迭代次数上次线性增长。
由于反事实值和期望值的差值是被添加到后悔值中而不是取代后悔值,所以玩家第一次随机行动(通常是一种差策略)仍会影响该后悔值。因此这种策略是一种面向未来而采取的策略。在一般的 CFR 方法中,第一次迭代的影响以 1/T 速率衰减,T 为迭代次数。为了快速削弱这种早期“坏”策略带来的影响,Pluribus 在早期迭代中采取线性 CFR 方法(在后续迭代中作者不采用这种方法,因为乘法带来的时间成本不值得这么做)。因此第一次迭代的影响将以如下速率衰减:
这使得策略得以在实战中更快改进,同时仍然保持着优良性能。
Pluribus 的蓝图策略在一台 64 核的服务器上计算了 8 天,没有使用 GPU,并且要求的内存小于 512GB,这在云计算高度发达的今天,仅仅只需要花费 144 刀!
不完全信息博弈中的深度限制搜索
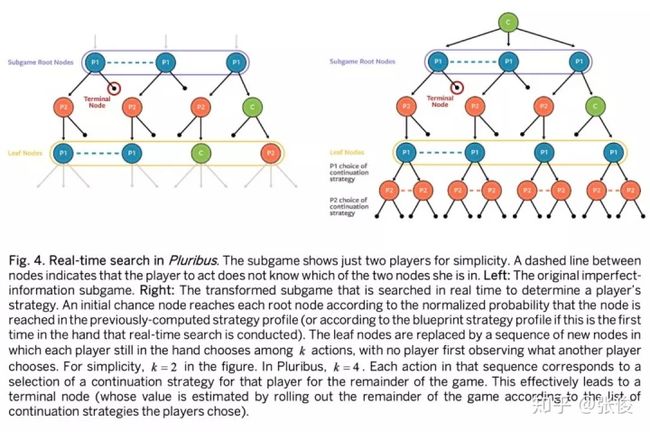
由于无限制德州扑克的规模和复杂性,整个游戏的蓝图策略必然是粗粒度的。Pluribus 仅仅在第一轮下注时根据蓝图策略进行游戏,其中决策点的数量足够小,以至于蓝图策略可以承受不使用信息抽象并且在动作抽象中选择更多动作。 在第一轮之后(即使在第一轮中,如果对手选择的赌注大小与蓝图动作抽象中的大小完全不同),Pluribus 也会进行实时搜索,以确定更好,更细粒度的策略。对于在第一轮稍稍偏离博弈树的对手投注,Pluribus 使用 pseudoharmonic mapping 将赌注映射到附近的 on tree 赌注上并继续根据蓝图进行游戏,就好像对手真的使用了这样的赌注大小。
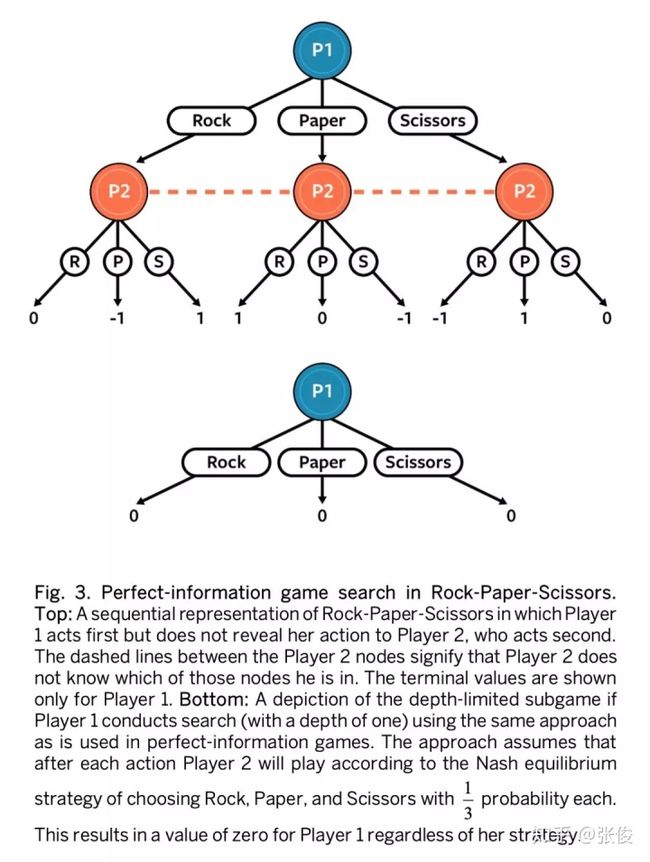
在许多完全信息博弈中实时搜索对于实现超人类表现是非常重要和必要的。这种情况下国际 AI 通常会向前看一些移动,直到在算法前瞻的深度限制处到达叶节点。原则上,如果 AI 可以准确地计算每个叶节点的值(例如取胜,平局或失败),则该算法将选择最佳的下一步动作。但是这样的搜索方法在不完全信息博弈中完全不适合。
例如,考虑一种顺序形式的石头剪刀布,如图 3 所示,其中玩家 1 首先行动但不向玩家 2 显示他的动作,然后玩家 2 动作。如果玩家 1 进行的搜索看起来只是前进一步,那么她的每一个动作都会导致一个零值的叶节点。毕竟,如果玩家 2 以选择纳什均衡策略(以 1/3 概率选择任意一个动作),则选择 Rock 的玩家 1 的值为零,选择剪刀的值也是如此。因此,如果玩家 2 的战略被固定为始终使用纳什均衡,那么对于玩家 1 总是出石头的确是一个最佳策略。然而,实际上,玩家 2 可以调整为总是出布。在这种情况下,总是出石头的价值实际上是 -1。
这个例子证明在不完美信息子博弈中,叶子节点没有固定值,相反,他们的值取决于探索者在子博弈中选择的策略。原则上,这可以通过让子博弈叶子节点的值作为搜索者在子博弈中的策略的函数来解决,但是这在大型游戏中是不切实际的。
Pluribus 使用一种新方法,其中搜索者明确地认为任何或所有玩家可以转移到子博弈的叶节点之外的不同策略。作者假设当到达叶子节点时,每个玩家可以在 k 个不同的策略之间进行选择以进行接下来的博弈。在本文中作者设定 k=4。第一种是预先计算的蓝图策略;第二种是一种改进的倾向于 folding 的蓝图策略;第三种是倾向于 calling 的蓝图策略;第四种是倾向于 raising 的蓝图策略。(以上 folding、calling、raising 均为牌桌策略,分别为弃牌、跟注和加注)
这种技术的引进将使得探索者找到更平衡的策略,因为选择不平衡策略(例如总是出石头)将被对手转移到其他策略(例如总是出布)惩罚。
在不完全信息博弈中搜索的另一个主要挑战是,玩家在特定情况下的最佳策略取决于从对手的角度看,玩家在每个情况下的策略是什么。为了应对这一挑战,Pluribus 根据其策略跟踪每副手牌可能达到当前状况的概率。 无论 Pluribus 实际持有哪手牌,它都会先计算出每一手牌的动作方式,小心平衡所有牌局的策略,以保持不可预测性。一旦计算出所有人的平衡策略,Pluribus 就会为它实际持有的牌执行一个动作。 在 Pluribus 中使用的深度限制的不完全信息子博弈的结构如图 4 所示。
Pluribus 使用两种不同形式的 CFR 来计算子博弈中的策略,具体取决于子博弈的大小和游戏进行的位置。如果子博弈相对较大或者在游戏的早期,则使用和蓝图策略一样的蒙特卡罗线性 CFR。否则,Pluribus 使用优化的基于矢量的线性 CFR 形式仅对机会事件(例如公共牌)进行采样。
实际测试时,Pluribus 仅仅使用了两台 Intel Haswell E5-2695 v3 CPU,仅占用小于 128G 的内存。相比而言,AlphaGo 对阵李世石时使用了 1920 块 CPU 和 280 块 GPU。在对每一个子博弈进行搜索时,根据现场情况,Pluribus 仅需要 1-33 秒。在其与自己镜像对抗的 6 人牌局中平均出牌时间为 20s,这远比顶尖人类选手快了近乎 2 倍。
实验
作者采用了两种模式评估 Pluribus 对阵人类选手。1、5 个顶尖人类选手 +1 个 AI (5H1 AI );2、1 个人类顶尖选手 +5 个 AI (1H5AI )。作者通过使用 AI 领域中的标准度量,mbb /game来衡量 AI 表现。该指标用来衡量每千手扑克平均赢得多少大盲注(Big Blind 大盲注 简称 BB 庄家左边第 2 个位置,牌局开始前需固定下注的位置,一般下注额为当前牌桌底注)。此外,作者利用 AIVAT 技术(variance-reduction technique)来减少游戏中的运气成分。
在 5H1AI 实验中,人类玩家和 AI 之间展开为期 12 天的 10000 手扑克比赛,在应用了 AIVAT 之后,Pluribus 平均每手赢 48 个 mbb(48 mbb/game)。若以每注 100 美元计算,Pluribus 每手可赢 5 美元,这远比人类玩家能达到的上限更高。在 1H5AI 中,Pluribus 平均以 32mbb/game 的速率将人类击败。
总结
Pluribus 这次出彩的表现使得 AI 玩耍多人多方游戏不再是难以逾越的鸿沟。也说明面对更复杂的情况和场景,即使难以取得理论支撑,倘若合理建模、合理设计算法,则从实践上先行突破也未必不可行。此外,人们潜意识中,训练=资源=烧显卡。此次 Pluribus 的成功无疑使得众多“科研平民”看到了希望和曙光。最后,Pluribus 成功应用于德扑也增强了科研工作者将 AI 推广于更复杂更广泛领域的信心。
参考文献
[1] Bowling, Michael, et al. "Heads-up limit hold’em poker is solved." Science 347.6218 (2015): 145-149.
[2] Brown, Noam, and Tuomas Sandholm. "Superhuman AI for heads-up no-limit poker: Libratus beats top professionals." Science 359.6374(2018):418-424.
[3] Brown, Noam, and Tuomas Sandholm. "Superhuman AI for multiplayer poker." Science (2019): eaay2400.
[4] Zinkevich, Martin A., Michael Bowling, and Michael Wunder. "The lemonade stand game competition: solving unsolvable games." ACM SIGecom Exchanges 10.1 (2011): 35-38.
#投 稿 通 道#
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢? 答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
投稿方式:
• 方法一:在PaperWeekly知乎专栏页面点击“投稿”,即可递交文章
• 方法二:发送邮件至:[email protected] ,所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。
加入社区:http://paperweek.ly
微信公众号:PaperWeekly
新浪微博:@PaperWeekly