【博弈论】势博弈(potential game)、EPG以及最佳响应、Nash均衡和帕累托(pareto)最优的理解
文章目录
- 前言
- 一、Potential game
- 二、Nash均衡和Pareto-optimal(帕累托最优)
-
- 1.Nash 均衡
- 2.Pareto最优
- 三、Best response(最佳响应)
- 四、Exact potential game(EPG)
-
- 1.合作-傀儡博弈
- 2.合作博弈
- 3.傀儡博弈
- 4.自激博弈
- 5.双边对称交互博弈
- 使用理解
前言
本文主要详细讲解potential game的概念以及Exact potential game 的定义和分类,以及这么博弈方法是如何在论文中引入并使用的,本文仅是对自己在该模块学习的一个总结,如果理解有误,还请批评指正,谢谢~
一、Potential game
Potential game即势博弈。在一场博弈中,每个用户可以做出自己的策略,并且通过调整策略使自己的效用(utility或者收益payoff)最大,假设这种通过调整策略得到的函数为效用函数,即Utility function,且与策略有关,我们写作 f ( s n ) f(s_n) f(sn),其中 s n s_n sn表示第n次出牌的策略。
由于我们建立该game的目的是让每个用户的效用最大,也就是每个用户对自己策略的改变一定的单调的,所以,假设每个用户的效用函数 f ( s n ) f(s_n) f(sn)的改变都能映射到一个势函数(Potential function)中,那么potential function也是单调的,此时将这种博弈称作势博弈。
定义:如果存在一个函数 p : S → R p: S\rightarrow R p:S→R, 满足任意 n ∈ N n \in N n∈N,有
U n ( s n ′ , s − n ) − U n ( s n , s − n ) = p ( s n ′ , s − n ) − p ( s n , s − n ) U_n(s_n',s_{-n})-U_n(s_n,s_{-n})=p(s_n',s_{-n})-p(s_n,s_{-n}) Un(sn′,s−n)−Un(sn,s−n)=p(sn′,s−n)−p(sn,s−n)
其中, s n ′ s_n' sn′表示不同于 s n s_n sn的策略,而 s − n s_{-n} s−n表示系统中其他用户的策略,具体如果要在代码中实现,可以理解为上一轮其他所有用户的策略集合,再以此得到自己本轮的策略。(不确定这样理解是不是对的,如有不对,望指正谢谢~)
二、Nash均衡和Pareto-optimal(帕累托最优)
这两种均是得到上述最优策略的方法。
1.Nash 均衡
用户通过不断改变自己的策略使自身的效用或收益最大,直到所有用户都满意,并不再改变策略为止,此时即为Nash(纳什)均衡,有:
U n ( s n ∗ , s − n ∗ ) ≥ U n ( s n , s − n ∗ ) U_n(s_n^*,s_{-n}^*)\ge U_n(s_n,s_{-n}^*) Un(sn∗,s−n∗)≥Un(sn,s−n∗)
Nash均衡的存在性和唯一性证明:
- 存在性:首先自变量 s n s_n sn是空间上非空闭合有界凸集,其次 U n ( s n , s − n ) U_n(s_n,s_{-n}) Un(sn,s−n)是在区间上拟凹或者拟凸的
- 唯一性:分为非负性、单调性以及可伸缩性
当然Nash均衡也有细分,分为纯策略(pure-strategy)纳什均衡和混合策略(mixed-strategy)纳什均衡,两者分别是纯策略的用户最优结果实现的均衡以及混合策略的用户最优结果实现的均衡,其中纯策略使指每个用户只做出一个策略选择并始终坚持这个策略;而用户使选择的策略随机化,并根据不同的重要性对每个策略制定一个概率,这种依据概率做出的策略即为混合策略。
2.Pareto最优
上述讲的势博弈以及nash均衡中的最优都是针对一个用户而言,用户根据自己的策略选择,使自身的效益最大化;但是pareto最优是使整体效益最优,谋求的是一个集体利益或者说社会福利最大化,因此pareto最优是指对每一个和效用最大的策略组合。
如果将囚徒困境的例子引入,
例子引用来源: https://blog.csdn.net/weixin_43903564/article/details/107196463
假设有两个小偷A和B联合犯事、私入民宅被警察抓住。警方将两人分别置于不同的两个房间内进行审讯,对每一个犯罪嫌疑人,警方给出的政策是:
- 如果一个犯罪嫌疑人坦白了罪行,交出了赃物,于是证据确凿,两人都被判有罪。如果另一个犯罪嫌疑人也作了坦白,则两人各被判刑8年。
- 如果另一个犯罪嫌人没有坦白而是抵赖,则以妨碍公务罪(因已有证据表明其有罪)再加刑2年,共10年,而坦白者有功被减刑8年,立即释放,即0年。
- 如果两人都抵赖,则警方因证据不足不能判两人的偷窃罪,但可以私入民宅的罪名将两人各判入狱1年。
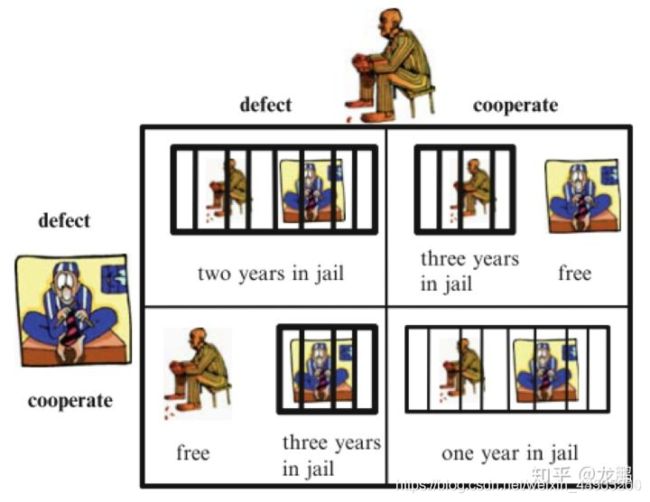
两人的选择见下表:表中的数字表示A,B各自的判刑结果:

如上所示,当两者都坦白时,是对自己最好的结果,此时针对Nash 均衡点即为(-8,-8)的点,但是如果针对pareto最优,就是两者都抵赖的为该最优点,即(-1,-1)。
三、Best response(最佳响应)
基于上述Potential game的定义,当通过调整策略使效用最大的点即为最优策略,下式即为最佳响应公式:
s n ∗ = arg max s n U n ( s n , s − n ) s_n^*=\mathop {\arg \max }\limits_{{s_n}} {U_n}({s_n},{s_{ - n}}) sn∗=snargmaxUn(sn,s−n)
四、Exact potential game(EPG)
针对上述Potential game的定义:
如果存在一个函数 p : S → R p: S\rightarrow R p:S→R, 满足任意 n ∈ N n \in N n∈N,有
U n ( s n ′ , s − n ) − U n ( s n , s − n ) = p ( s n ′ , s − n ) − p ( s n , s − n ) U_n(s_n',s_{-n})-U_n(s_n,s_{-n})=p(s_n',s_{-n})-p(s_n,s_{-n}) Un(sn′,s−n)−Un(sn,s−n)=p(sn′,s−n)−p(sn,s−n)
如果 U n U_n Un处处可微,则严格势博弈(EPG)的充分条件为:
∂ 2 U i ( s ) ∂ s i ∂ s j = ∂ 2 U j ( s ) ∂ s j ∂ s i , i , j ∈ N \frac{{{\partial ^2}{U_i}(s)}}{{\partial {s_i}\partial {s_j}}} = \frac{{{\partial ^2}{U_j}(s)}}{{\partial {s_j}\partial {s_i}}},i,j\in N ∂si∂sj∂2Ui(s)=∂sj∂si∂2Uj(s),i,j∈N
可以理解为严格势博弈是势博弈的一种,并且当满足上式时,为严格势博弈,因此严格势博弈也一样满足效用函数之差等于势函数之差。同时严格势博弈主要分为以下5中博弈:
以下参考《博弈论》书籍,具体哪个作者忘记了
1.合作-傀儡博弈
如果博弈的所有参与者的效用函数可以用 U n ( s ) = C ( s ) + D n ( s − n ) U_n(s)=C(s)+D_n(s_{-n}) Un(s)=C(s)+Dn(s−n)表示,其中 C ( s ) C(s) C(s)与n无关,则其势函数为: p = C ( s ) p=C(s) p=C(s)
C ( s ) C(s) C(s)定义了一个合作函数,所有博弈参与者对于具有的策略s都会得到相应的回报, D n ( s − n ) D_n(s_{-n}) Dn(s−n)定义了一个傀儡函数,参与者n的结构不依赖于自身的策略,而是依赖于其他参与者的策略
由于满足: U n ( s n ′ , s − n ) − U n ( s n , s − n ) = C ( s n ′ , s − n ) − C ( s n , s − n ) U_n(s_n',s_{-n})-U_n(s_n,s_{-n})=C(s_n',s_{-n})-C(s_n,s_{-n}) Un(sn′,s−n)−Un(sn,s−n)=C(sn′,s−n)−C(sn,s−n),故C(s)为该博弈的势函数。
2.合作博弈
即只有合作函数,因此上述 D n ( s − n ) = 0 D_n(s_{-n})=0 Dn(s−n)=0,即 U n ( s ) = C ( s ) U_n(s)=C(s) Un(s)=C(s)
3.傀儡博弈
即只有傀儡函数, U n ( s ) = D n ( s − n ) U_n(s)=D_n(s_{-n}) Un(s)=Dn(s−n), C ( s ) = 0 C(s)=0 C(s)=0,此时傀儡博弈的势函数都是一个常函数。
4.自激博弈
如果所有的博弈者都有如下的效用函数,那么这种类型的博弈就叫做自激博弈:
U n ( s ) = K n ( s n ) U_n(s)=K_n(s_n) Un(s)=Kn(sn)
其中 K n : s n → R K_n: s_n \rightarrow R Kn:sn→R, 由于博弈被定义为一种相互影响的决策过程,而自激博弈确是没有相互影响的交互过程,因此严格上说不算是博弈,其势函数为:
P = ∑ n ∈ N K n ( s n ) P=\sum\limits_{n\in N}K_n(s_n) P=n∈N∑Kn(sn)
5.双边对称交互博弈
如果每个博弈的参与者的效用函数都可以表达如下的形式:
U i ( s ) = ∑ j ∈ N w i , j j ( s i , s j ) − K i ( s i ) U_i(s)=\sum\limits_{j\in N}w_{i,j}~j(s_i,s_j)-K_i(s_i) Ui(s)=j∈N∑wi,j j(si,sj)−Ki(si)
其中 w i , j w_{i,j} wi,j为双边交互函数, K i K_i Ki为自利函数,如果对于所有 ( s i , s j ) ∈ S i × S j (s_i,s_j) \in S_i \times S_j (si,sj)∈Si×Sj,有 w i , j ( s i , s j ) = w i , j ( s j , s i ) w_{i,j}(s_i,s_j)=w_{i,j}(s_j,s_i) wi,j(si,sj)=wi,j(sj,si), 那么这种博弈称为双边对称博弈,其势函数为:
p ( s ) = ∑ i ∈ N ( ∑ j = 1 i − 1 w i , j j ( s i , s j ) − K i ( s i ) ) p(s)=\sum\limits_{i \in N}(\sum\limits_{j=1}^{i-1}w_{i,j}~j(s_i,s_j)-K_i(s_i)) p(s)=i∈N∑(j=1∑i−1wi,j j(si,sj)−Ki(si))
其中第一项是交互部分,后一项是仅关于i的部分。
使用理解
首先要证明建立的游戏理论模型符合势博弈的定义,其次要证明存在Nash均衡点,并根据不断调整策略(迭代的过程)利用最佳响应得到Nash均衡点(即最优策略)以及最大的效用。其中势函数的建立过程可以证明是否符合EPG,并根据具体的博弈模型建立势函数,也可以直接自己找到具体的对应关系。