传统多用户MISO系统中的加权和速率WSR最大化问题,(优化AP的beamformingW)
本文是简单记录一下对文章Weighted Sum-Rate Maximization for
Reconfigurable Intelligent Surface Aided Wireless
Networks的学习
信道模型
AP有M个天线(ULA),RIS有N个天线(UPA),一共K个单天线用户

信道模型是常见的RIS辅助通信的信道模型
信道估计
- Brute-Force
- Compressive-Sensing
- Semi-passive RIS
1 BruteForce 每次只有一个RIS element开着其他关闭,AP依次估计。缺点是训练开销巨大(与N成比例)。然后,在[38]中,通过将相邻元素分组来修改该方法以减少训练开销。
2 Compressive-Sensing Method:通过利用RIS辅助链路的低秩特性来进一步减少训练开销
3 Semi-passive:在[40]中,通过在RIS上集成具有信道估计能力的有源元件,提出了半无源结构。最后,证明了利用深度学习和压缩感知工具,训练开销可以变得微不足道。
问题建构
perfect CSI
imperfect CSI
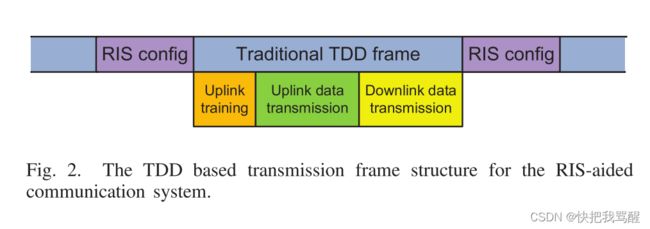
基于TDD的传输帧结构
在两个传统TDD传输帧之间插入一个用于RIS配置的时隙。 θ θ θ配置完成后,其余系统设计与传统通信系统完全相同。
AP需要通过信道估计得到的信道信息:

其维数为M(与N无关)。我们仍然假设所有用户都完全知道hk。
然而,为了配置 θ θ θ,信道系数 h d , k h_{d,k} hd,k, G G G和 h r , k h_{r,k} hr,k应单独估计。
然而(恼)
- 根据章节II-B中的参考文献,难以利用短的训练导频来高精度地估计这些信道系数。
- 用于信道估计的导频和数据符号都来自先前的上行链路传输时隙,这也引入了估计误差。
因此假设非理想信道估计的误差为:
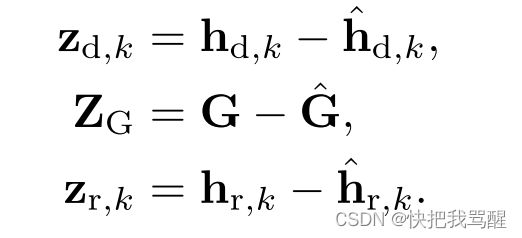
如果应用最小均方误差(MSE)估计,则误差 z d , k z_{d,k} zd,k、 Z G Z_G ZG和 z r , k z_{r,k} zr,k与估计的信道系数 h d , k ^ \hat{h_{d,k}} hd,k^, G ^ \hat{G} G^和 h r , k ^ \hat{h_{r,k}} hr,k^不相关[43]-[45]。然后,可以将输入数据传输帧中的真实信道系数 h d , k h_{d,k} hd,k, G G G和 h r , k h_{r,k} hr,k建模为来自受不完善CSI知识 h d , k ^ \hat{h_{d,k}} hd,k^, G ^ \hat{G} G^和 h r , k ^ \hat{h_{r,k}} hr,k^和信道估计误差的分布 z d , k z_{d,k} zd,k、 Z G Z_G ZG和 z r , k z_{r,k} zr,k支配的样本空间 F ≜ { h d , k ( ξ ) , G ( ξ ) , h r , k ( ξ ) , ∀ k , ∀ ξ } \mathcal{F} \triangleq\left\{\mathbf{h}_{\mathrm{d}, k}(\xi), \mathbf{G}(\xi), \mathbf{h}_{\mathrm{r}, k}(\xi), \forall k, \forall \xi\right\} F≜{hd,k(ξ),G(ξ),hr,k(ξ),∀k,∀ξ}的实现,其中ξ表示从F中提取的随机实现的索引

如果CSI是完全估计的,则 h d , k h_{d,k} hd,k, G G G和 h r , k h_{r,k} hr,k对不同的ξ保持常数。
与已有的研究相比,该方案的优点在于,RIS系统的配置只需对传统无线系统做很小的改动。然而,P(B)是具有内层变量W(ξ)的随机优化问题,并且外层变量θ,内层和外层子问题都是非凸的,没有封闭解。另外,目标函数中含有期望算子,样本空间F的概率密度函数通常很复杂,也没有封闭式的表达式。因此,设计求解P(B)的算法是一项具有挑战性的任务。
交替优化方法(ALTERNATING OPTIMIZATION)
采用两块BCD(块坐标下降)
其基本思想是将优化变量分解为几个块,然后按照一些特定规则更新每个块,同时将剩余块固定在其最后更新的值[46]。
在现有工作[22]和[24]中,交替优化方法通常用于解决RIS辅助系统中的联合优化问题。特别地,联合优化问题被分解为两个子问题:一个是AP处的常规波束成形设计问题,另一个是给定优化波束成形向量的相位优化问题
算法带入本情景的具体描述
当θ固定时,优化W的子问题转化为传统多用户MISO系统的WSR最大化问题。
文献中已经对该问题进行了广泛研究,获得平稳解的一种著名方法是WMMSE算法,其迭代更新规则如下【47】:

WMMSE
参考链接
https://zhuanlan.zhihu.com/p/358642721
Q. Shi, M. Razaviyayn, Z. Luo, and C. He, “An iteratively weighted
MMSE approach to distributed sum-utility maximization for a MIMO
interfering broadcast channel,” IEEE Trans. Signal Process., vol. 59,
no. 9, pp. 4331–4340, 2011.





PS: Woodbury Matrix Identity and Sherman-Morrison Formula是什么
Woodbury matrix identity
In mathematics (specifically linear algebra), the Woodbury matrix identity, named after Max A. Woodbury,[1][2] says that the inverse of a rank-k correction of some matrix can be computed by doing a rank-k correction to the inverse of the original matrix. Alternative names for this formula are the matrix inversion lemma, Sherman–Morrison–Woodbury formula or just Woodbury formula. However, the identity appeared in several papers before the Woodbury report.[3][4]
The Woodbury matrix identity is[5]:
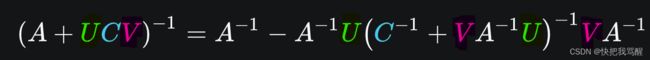
where A, U, C and V are conformable matrices: A is n×n, C is k×k, U is n×k, and V is k×n.
While the identity is primarily used on matrices, it holds in a general ring or in an Ab-category.
https://en.wikipedia.org/wiki/Woodbury_matrix_identity




