408数据结构学习笔记——顺序查找、折半查找、分块查找

目录 

1.顺序查找  

1.1.顺序查找的概念

1.2.顺序查找的代码

1.3.顺序查找的查找效率

1.4.顺序查找的优化

1.5.顺序表的时间复杂度

2.折半查找

2.1.折半查找的概念

2.2.折半查找的代码

2.3.折半查找的查找效率​

2.4.折半查找判定树的构造

3.分块查找

3.1.分块查找的概念

3.2.分块查找手算过程

3.2.1.顺序查找索引表

3.2.2.折半查找索引表

3.3.分块查找效率分析

4.王道课后题

---

1.顺序查找  

1.1.顺序查找的概念

通常用于线性表，从表中第一个元素开始，逐一检查当前元素是否满足条件

1.2.顺序查找的代码

typedef struct{
    elemtype *elem;    //动态数组的首地址
    int tableLen;    //表长
}SSTable;

//顺序查找
int Search_Seq(SSTable ST, elemtype key){
    int i;
    //从头逐一查找表中元素
    for (i = 0; i < ST.tableLen && ST[i] != key; i++);
    //判断i是否等于表长
    if (i == St.tableLen) return -1;
    else return i;
}

1.3.顺序查找的查找效率

查找成功时，平均查找长度为ASL = n - i + 1

查找失败时，平均查找长度为ASL = n + i

1.4.顺序查找的优化

1.在有序表中若是从小到大排列，当发现第 i 个元素的大小已比key更大时，就可以跳出循环，return -1

2.顺序表中给个元素的被查概率不相等，则按被查概率依次存放

1.5.顺序表的时间复杂度

O(N)

2.折半查找

2.1.折半查找的概念

仅使用于有序的线性表（只能以顺序存储）

若各个元素并非等概率出现，折半查找性能并不一定优于按出现概率降序排列的顺序查找

算法思想：

1.申明三个指针low, high, mid，low指向数组的第一个元素，high指向数组的最后一个元素，mid指向(high + mid) /2 （向下取整）

2.通过mid和key的对比判断key在数组中的位置，如果mid更大，则key在mid的左边，且key在数组的范围为(low, mid - 1)；如果key更大，则key在mid的右边，且key在数组的范围为(mid + 1, high)

3.修改low和high的指针，分别指向范围的下限和范围的上限（缩小范围），继续查找，直到找到为止

2.2.折半查找的代码

int Binary_Search(elemtype arr[], elemtype key, int length){
    //初始化high为数组最后一个元素的数组下标，low为0
    int high = length - 1, low = 0, mid;
    while (low <= high){
        //每次循环开始的时候，重置mid指针为high和low的中间值
        mid = (high + low) / 2;
        //当前mid指向的元素为key时，查找成功，返回mid
        if (arr[mid] == key) return mid;
        //mid比key小，去mid的右半区查
        else if (arr[mid] < key) low = mid + 1;
        //mid比key大，去mid的左半区查
        else high = mid - 1;
    }
    //结束循环时，说明数组中没有key值，查找失败，返回-1
    return -1;
}

2.3.折半查找的查找效率

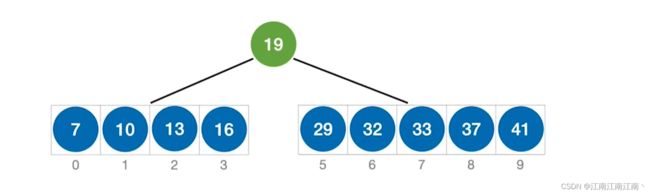
查找成功（到绿色点）：最多查找4次 ASL = (1 * 1 + 2 * 2 + 3 * 4 + 4 * 4) / 11 = 3

因为折半查找只有最后一层未满的特性，n - 1层都是满的（满二叉树），因此，在计算查找成功时，可以利用这一特性方便计算

计算时：

1 ~ n - 1：层 同结构满二叉树同层结点数 * 当前层数

n 层：（总结点数 - （n - 1）层总结点数）* 当前层数

查找失败（到紫色点）：最多查找5次 ASL = (3 *  4 + 4 * 8) / 12 = 11 / 3

查找失败时只需查找到绿色结点，不需要到紫色结点再比较一次

计算时：最后一层的结点数 * 层数 + （同结构满二叉树 - 最后一层结点数） * （层数 - 1）

2.4.折半查找判定树的构造

当前若low和high之间的个数为奇数个，则mid分割后，左右子树的个数相等

当前若low和high之间的个数为偶数个，则mid分割后，右子树的个数比左子树大1

1.折半查找判定树中，对于任何一个结点，则都有左子树结点数 - 右子树结点数 = 0 或 1 （平衡二叉树）（构造判定树中，仅需根据这一特性每次找到当前子树的根节点划分左右子树）

2.折半查找判定树中，只有最下面一层是不满的，且树高为h = log(n+1)向上取整

3.失败结点为n - 1个（成功结点的空链域的数量）

4.结点关键字中，左 < 中 < 右（排序二叉树类似，但是排序二叉树可能会出现单支的情况，最坏时间复杂度为O(n)；而折半查找判定树一定是平衡树）

5.折半查找的查找成功和查找失败的次数均不超过树高，因此，时间复杂度为O(logn)

6.折半查找的时间复杂度虽然比顺序查找低，但是并非在任何情况下其查找效率都更高

7.最少查找次数每次都去结点最少的子树，最多查找次数每次都去结点最多的子树

3.分块查找

3.1.分块查找的概念

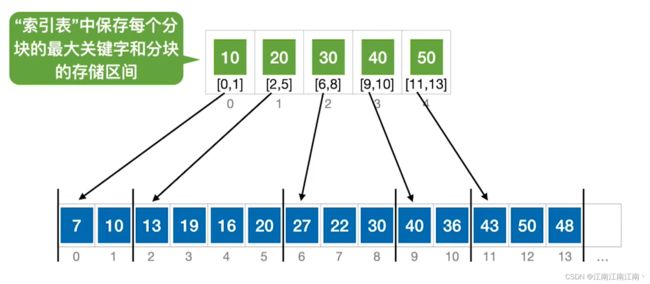
为数组建立一个索引表，并将数组分割成为若干个块，索引表中一次存放每个块内的最大值和块内元素的存储区间（块内无序，块间有序）

分块查找的过程：

1.在索引表中确定key所属的分块（索引表可以采用顺序查找，也可以采用折半查找）

2.在块内查找（非有序，只能顺序查找）

3.2.分块查找手算过程

3.2.1.顺序查找索引表

以查找36为例

1.在索引表中依次遍历找到第一个大于它的值，即40

2.移动到40指向的数组区间的第一个元素，即数组下标9

3.从数组下标9开始遍历，40→36 找到36

以查找17为例

1.在索引表中依次遍历找到第一个大于它的值，即20

2.移动到20指向的数组区间的第一个元素，即数组下标2

3.从数组下标2开始遍历，13→19→16→20

4.此时移动到20，数组下标为5，到索引表中17的最后一个元素，仍匹配失败，说明表中没有17

3.2.2.折半查找索引表

索引表只是保存元素的数组区间，方便在数组中寻找元素（相对位置），就算在索引表上找到相应元素，还是得再去数组中重新再找一次

以查找30为例

1.low指向10，high指向50，mid = (low + high) / 2 指向 2，即指向30

2.到30所指向的数组区间依次查找

以查找19为例

1.low指向10，high指向50→mid指向30，mid > key ， high = mid - 1

2.low指向10，high指向20→mid指向10，mid < key，  low = mid + 1

3.low指向20，high指向20→mid指向20，mid > key，  high = mid - 1

4.low指向20，high指向10→low > high 折半查找结束

5.到low所指向的元素区间进行逐一遍历查找

去low指向区间查找的原因：最后low的左边一定小于key，而分块查找的索引表存放的是每块的最大值

除了能在key能在索引表上直接找到，否则都要执行到low > high，才能确定key元素所可能存在的数组区间范围

3.3.分块查找效率分析

分块查找的平均查找长度分为索引表查找L1和块内查找L2

设所有元素被均匀的分为b块，每块内有s个元素

索引表顺序查找：L1 =    L2 =  →ASL = 

当块内元素为时，ASL取最小值为

索引表折半查找：L1 = log(b + 1) 向上取整 L2 = (一般不考）

可以对分块查找的索引表和块内元素都采用折半查找

4.王道课后题

1.平均查找长度不同。设查找元素为k，有序顺序表若找到第一个大于k的元素，就可以结束函数，返回查找失败；而无序表每次都需要遍历完整个表

2.平均查找长度相同。两个表中都是找到k就停止，返回查找成功

3.平均查找长度不同。有序表仅需找到第一个等于k的元素后，设该元素位序为p，再往后遍历找到第一个不等于k的元素，设该元素位序为q，则p ~ q - 1为表中所有值为k的元素，无需遍历整个表；而无序表中每次都需要遍历表中所有元素

2.275：509→154→275        684：509→677→897→765

3.查找成功的平均查找长度：(1 * 1 + 2 * 2 + 4 * 3 + 7 * 4) / 14 = 45 / 14

查找失败的平均查找长度：(1 * 3 + 14 * 4) = 59 / 14

int k_search(int arr[], int n, int k, int key){
    int left = 0, right = n, mid = k / n;
    while (left <= right){
        mid = k / n;
        if (arr[mid] == key) return arr[mid];
        else if (arr[mid] < key) right = k - 1;
        else left = k + 1;
    }
    return -1;
}

参考折半查找，O()

2.每8个元素进行一轮顺序查找，确定元素所在的区间，顺序查找的平均查找长度为 (n + 1) / 2 

进入8k ~ 8(k+1) - 1的区间内，分为两种：

（1）顺序查找（每轮八个元素的最后一个元素）的平均查找长度：1

（2）折半查找（前七个元素构成的折半查找判定树）：(1 * 1 + 2 * 2 + 4 * 3) = 16

每个关键字查找成功的概率为1 / 8

因此，结果为： (n + 1) / 2 +(1 + 16) / 8

int Binary_Search(int arr[], int left, int right, int key) {
    //temp变量保存当前结果
    int temp = -2;
    //当前没有结果且还未遍历完数组
    if (left <= right) {
        //重置mid
        int mid = (left + right) / 2;
        //mid = key，返回mid的下标
        if (key == arr[mid]) temp = mid;
        //mid比key大，去右子树
        else if (key < arr[mid]) temp = Binary_Search(arr, left, mid - 1, key);
        //mid比key小，去左子树
        else temp = Binary_Search(arr, mid + 1, right, key);
    }
    //当前没有结果遍历完数组，返回-1表示查找失败
    else temp = -1;
    //返回结果
    return temp;
}

int SearchEntrance(int arr[], int n, int key) {
    int left = 0, right = n - 1;
    //用res保存key元素的数组下标
    int res = Binary_Search(arr, left, right, key);
    return res;
}

//顺序结构
int Search_Exchange(int arr[], int key, int n){
    int res = -1, i = 0;
    //第一个元素为key时
    if (arr[0] == key) {
        res = 0;
        return res;
    }
    //从第二个元素开始遍历数组
    for (i = 1; i < n; i++){
        if (arr[i] == key) {
            //将第i个元素前移一位
            int temp = arr[i - 1];
            arr[i - 1] = arr[i];
            arr[i] = temp;
            res = i;
        }//if
    }//for
    //返回key元素更改后的数组下标
    return res;
}            

//链式结构
typedef struct LNode{
    struct LNode *next;
    elemtype data;
}LNode, *LinkList;

LNode *Search_Exchange(LinkList &L, elemtype e){
    LNode *p = L, *pre = L = NULL;
    while(p->next){
        //e元素是链表的一个元素，无需修改前驱，返回其地址
        if (p->next->data == e){
            if (p == L) return p->next;
            else {
                //修改pq的相对位置
                LNode *q = p->next;
                pre->next = q;
                p->next = q->next;
                q->next = p;
        }//if
        else{
            pre = p;
            p = p->next;
        }
    }//while
    //表中没有指定元素
    return NULL;
}

 

1、2都采用概率降序依次存储元素，平均查找长度为2.1

若元素出现非等概率，折半查找并非一定优于顺序查找（概率降序）