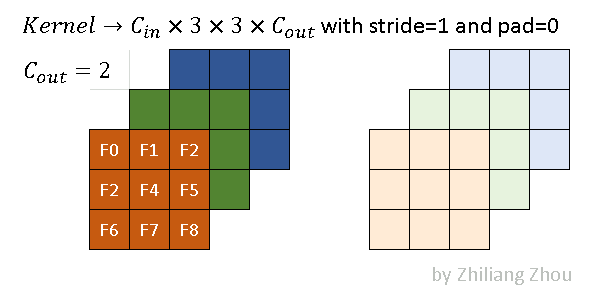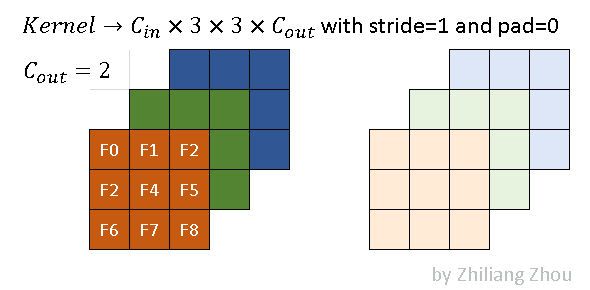Second 算法目标检测

SECOND

Sparsely Embedded Convolutional Detection 稀疏嵌入卷积检测

动机

• 考虑到VoxelNet论文在运算过程中运算量较大，且速度不佳。作者引入了稀疏3D卷积去代替VoxelNet中的3D卷积层，提高了检测速度和内存使用；
• VoxelNet论文有个比较大的缺点就是在训练过程中，与真实的3D检测框相反方向的预测检测框会有**较大的损失函数，**从而造成训练过程不好收敛。

创新点

• 比如数据增强这块，作者使用了数据库采样的操作；
• 对于正负样本数量的极度不平衡问题，作者借鉴了RetinaNet中采用的Focal Loss；
• 提出了一种新颖的角度损失回归方法，该方法展示了比其他方法更好的方向回归性能。

稀疏卷积

why?

• 卷积神经网络已经被证明对于二维图像信号处理是非常有效的。然而，对于三维点云信号，额外的维数 z 显著增加了计算量
• 与普通图像不同的是，大多数三维点云的体素是空的，这使得三维体素中的点云数据通常是稀疏信号

详解

稀疏信号采用数据列表和索引列表表示，二维和三维稀疏信号没有本质区别

1. 定义

   

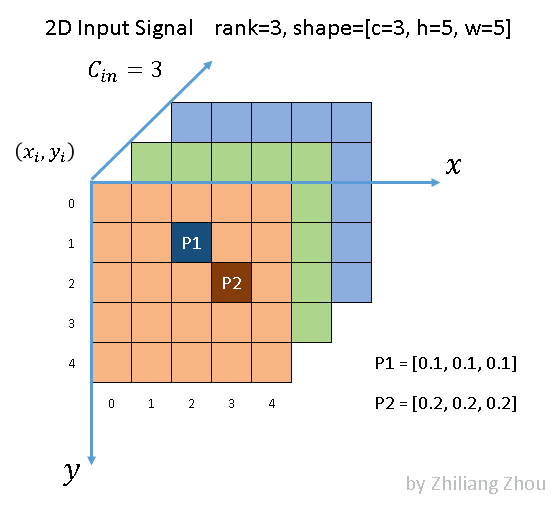
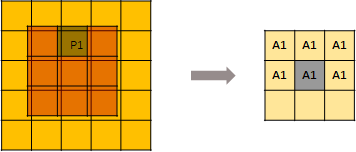
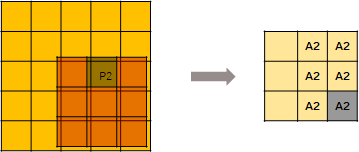
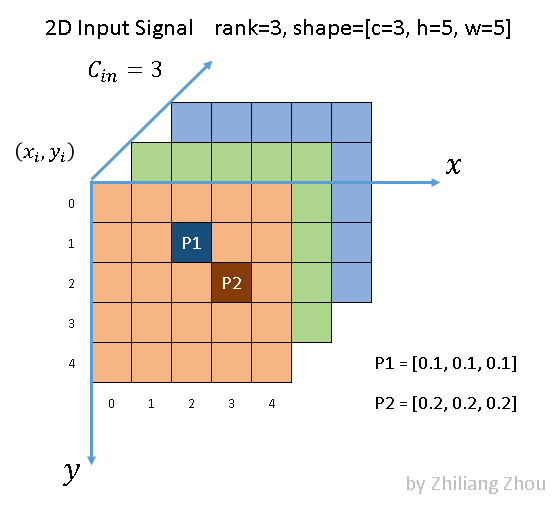
   ​ 如图所示，我们有一个5 × 5的3通道图像。除了 P1和 P2两点外，所有像素都是(0,0,0) （虽然0这个假设也很不严谨）

   ​ 在稀疏格式中，数据列表是[[0.1,0.1,0.1] ，[0.2,0.2,0.2] ，索引列表是[1,2] ，[2,3] ，并且是 YX 顺序。

2. kernel核定义

​ 稀疏卷积的卷积核与传统的卷积核相同。上图是一个例子，其内核大小为3x3。

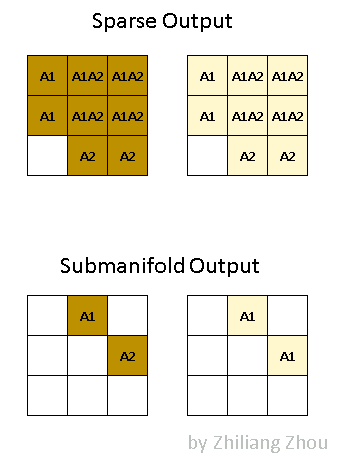
3. 输出的定义

   • 一种是 regular output definition，就像普通的卷积一样，只要kernel 覆盖一个 active input site，就可以计算出output site。

   • 另一个称为submanifold output definition。只有当kernel的中心覆盖一个 active input site时，卷积输出才会被计算。

     

     1代表 active site，即 P1产生的卷积结果。

     类似地，A2代表从 P2计算出的 active site。A1A2代表 active site，它是 P1和 P2输出的总和。

     深色和浅色代表不同的输出通道。

计算过程

1. 构建 Input Hash Table 和 Output Hash Table

   现在要把 input 和 Output 都表示成 hash table 的形式

   

   input hash table和output hash table 对应上图的 Hash_in，和 Hash_out。

​ 对于 Hash_in：

​ v_in 是下标，key_ in 表示value在input matrix中的位置

​ 现在的input一共两个元素 P1和P2，P1在input matrxi的(2, 1)位置, P2在 input matrix 的(3,2)的位置，并且是 YX 顺序

​ 是的没错，这里只记录一下p1的位置 ，先不管 p1代表的数字。所以其实可以把这个input hash table命名为 input position hash table

​ input hash tabel的构建完成了，接下来构建 output hash table。

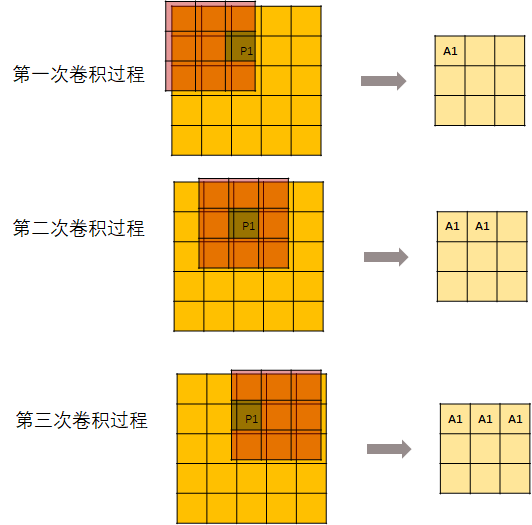
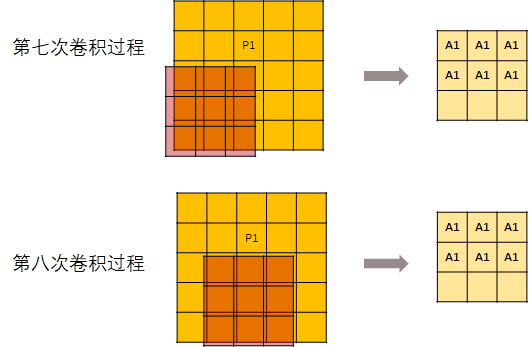
​ 先来看一下卷积过程中 P1是怎么向下传导的

​ 用一个kernel去进行卷积操作：

​

​ 但是，并不是每次卷积kernel都可以刚好碰到P1。所以，从第7次开始，输出的这个矩阵就不再变化了。

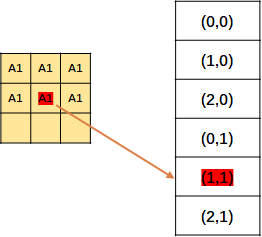
​ 然后记录每个元素的位置。

​ 上面说的只是操作P1，当然P2也是同样的操作。

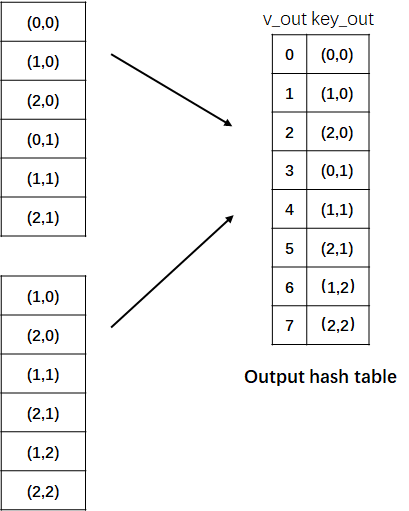
​ 然后把P1, P2的结果结合起来（主要是消除掉重复元素），得到了一张位置表。是的没错，此处记录的还是位置。

​ 然后编号，就得到了 output hash table。

2. 构建 Rulebook

   第二步是建立规则手册——rulebook。

   这是稀疏卷积的关键部分！！！ （敲黑板了）

   规则手册的目的类似于 im2col [5] ，它将卷积从数学形式转化为有效的可编程形式。

   但是与 im2col 不同的是，rulebook集合了卷积中所有涉及到的原子运算，然后将它们关联到相应的核元素上。

   

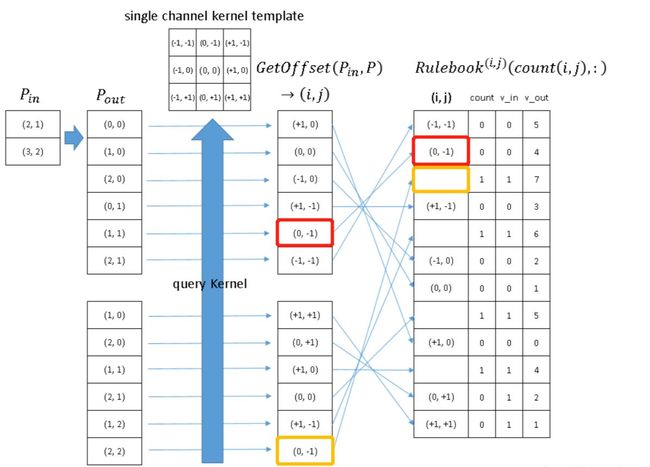
   上图就是如何构建 rulebook 的例子。

   rulebook的每一行都是一个 atomic operation（这个的定义看下面的列子就知道了），rulebook的第一列是一个索引，第二列是一个计数器count， v_in和 v_ out 分别是atomic operation的 input hash table 的 index和 output hash tabel的index。（没错，到现在为止，依然是index，而没有用到真实的数据。）

   atomic operation是什么呢？举个例子

   

   红色框框表示的是下图的atomic operation

   

   黄色框框表示的是下图的atomic operation

   

   因为这个时候(0, -1) 是第二次被遍历到，所以count+1.

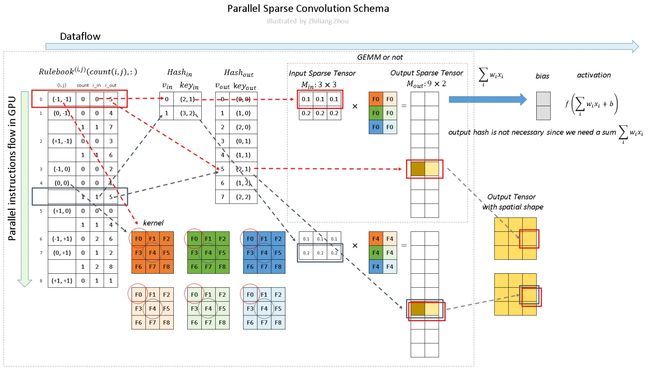
   3. Computation Pipeline

      综上，编程中的过程是什么样子的呢？

      现在有输入（这个图上面出现过了）

      

      对它进行卷积操作

      

      深色和浅色的kernel表示2个不同的kernel，即output channel=2。则，程序里的稀疏卷积过程是

      

      如图所示，稀疏卷积中的卷积计算，不用滑动窗口方法，而是根据rulebook计算所有的原子操作。在图中，红色和蓝色箭头表示两个不同的计算实例。

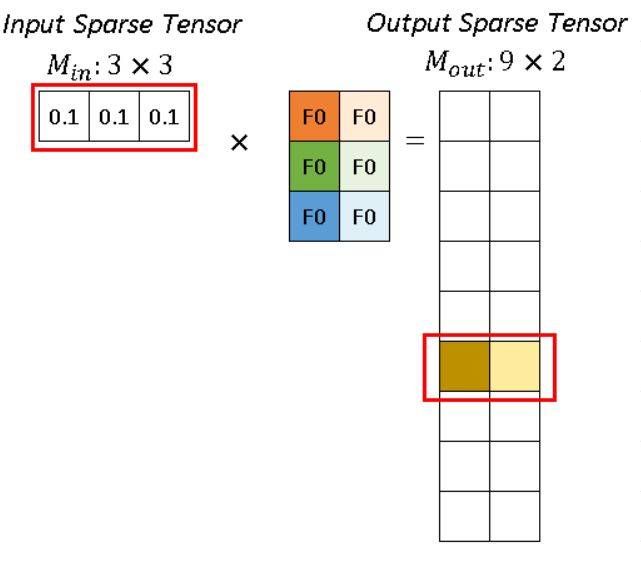
      红色箭头处理rulebook中第一个 atomic operation。从rulebook中，我们知道这个atomic operation 有来自 input index (v_in) =0 位置(2,1)的 P1 的输入，和 output index (v_out) =5 位置 (2,1)的输出。

      

      对于p1 代表的 (0.1, 0.1, 0.1)，分别跟深色和浅色两个kernel进行卷积运算，得到深黄色和浅黄色两个channel的输出。

      同样，蓝色箭头表示另一个原子操作。

      可以看到红色操作和蓝色操作有相同的output index (v_out），没事的，直接把他们的输出加起来就好了。

      稀疏卷积总结

      input/output hash tabel只维护那些真正有元素的条目。

      所以说，稀疏卷积是非常 efficient的，因为我们只计算非零元素（元素指的是像素 或者 体素）的卷积，而不需要计算所有的元素。

      虽然构建 rulebook 也是需要额外的计算开销的，但是这个构建过程也是可以在GPU上并行处理的。

   方向回归

   SECOND中还有一个重要的创新，就是对物体方向估计进行了重新的建模。

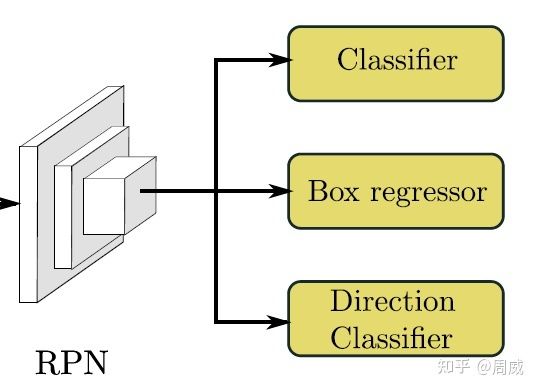
   作者在最后的RPN层（原来是两个分支，用来物体分类和位置回归）多引入了一个分支（如下图5所示），用来对物体方向进行分类。

   

   在VoxelNet中，一个3D BBox被建模为一个7维向量表示，分别为$（x_c,y_c,z_c,l,w,h,\theta ）$

   训练过程中，对这7个变量采用Smooth L1损失进行回归训练。

​ 当同一个3D检测框的预测方向恰好与真实方向相反的时候，上述的7个变量的前6个变量的回归损失较小，而最后一个方向的回归损失会很大，这其实并不利于模型训练。为了解决这个问题，作者引入了对方向角的回归损失，定义如下：
$$L_{\theta }=SmoothL1(\sin ({\theta }_p-{\theta }_t))$$
​ 为预测的方向角， ${\theta }_t$ 为真实的方向角。

​ 那么当$${\theta }_p={\theta }_t\pm \pi$$ 的时候，该损失趋向于0，这样更利于模型训练。

​ 这时候大家可能会问了，那这样的话，模型预测方向很可能与真实方向相差180度呀。

​ 这时候作者提出了另一种解决方法（也就是RPN中的direction classifer分支），作者将车头是否区分正确直接通过一个softmax loss来进行约束。如果theta>0则为正，theta<0则为负。那么这就是个简单的二分类问题了，也就是结构图中direction classifer。

目标函数

整体的目标函数如下:
$$L_{total}={\beta }_1{L}_{cls}+{\beta }_2(L_{reg-\theta }+L_{reg-other})+{\beta }_3{L}_{dir}$$

1. sine-Error Loss for Angle Regression
   voxelnet 直接预测弧度补偿,面临着一个角度相反的问题(adversarial example problem)，比如0度和180度。它们两个角度相反，但是bounding box都是一样的，如果误识别了，会导致loss很大。因此提出了sin-Error loss:
   $$L_{\theta }=SmoothL1(sin({\theta }_p-{\theta }_t))$$

   $${\theta }_p$$ 是预测值。

​ 这个loss 有两个优点:

• 解决了adversarial example problem。
• 它自然地根据角度偏移函数对IoU进行建模

2. direction loss

​ 上面的angle loss 把相反的bounding box视为一样，则在direction loss 使用了 softmax loss 进行区分。如果yaw 旋转相对于真值的z轴大于0，则为positive, 否者为negative。

3. classification loss
   分类使用的是focal loss。

$$FL(p_t)=-\alpha (1-p_t{)}^{\gamma }log(p_t)$$