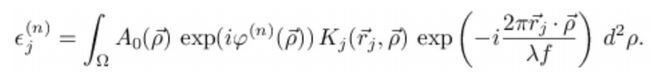多颗微粒的阵列光镊系统设计
张毅群 卢昱丞 许海东 刘琦
杭州电子科技大学12级光信息科学与技术专业光电检测课程项目,张毅群小组技术调研报告。
1 光镊技术介绍
1.1 光镊技术定义
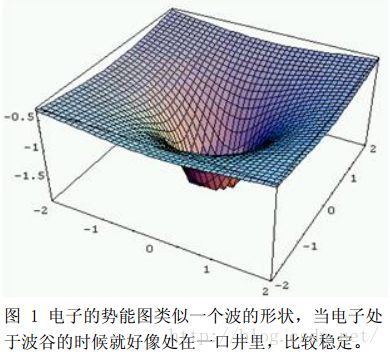
光镊(Optical tweezers),又称为单光束梯度力光阱(single-beam optical gradient force trap),是利用光与物质间动量传递的力学效应(主要为光强梯度力)而形成的三维势阱来捕获和操纵微粒的技术。
如图1所示,这种由光形成的光学势阱就像一个具有引力的陷阱,微粒一旦处在陷阱中,如果没有足够大的动能就很难逃脱,它就像一把镊子可以把微粒牢牢钳住[1],因此形象地称它为光镊。
1.2 基本原理
我们以透明介质小球作模型,用几何光学来讨论光与物体的相互作用,阐述一下光镊是如何捕获微粒的,如图2所示。
说明:虽然处理光与微粒的相互作的用,严格地说应该用光的电磁理论[2]。特别是对于尺寸小于光波长的粒子。但是为了阐明梯度力的概念,并形象地揭示出光是如何捕获微粒的,本文就以直径大于光波长的透明介质小球为对象,采用几何光学的原理,近似地分析光作用于物体所产生的力[2]。
1.2.1 光的传播过程
如图2(a)所示,一束激光经透镜聚焦后,入射光线A将光子的动量以辐射压得形式作用于粒子小球,A经过两次折射后,光子动量发生改变,以光线A′出射[1]。
1.2.2小球受力分析
如图 2(b),光束的动量变化为△,根据动量守恒定律,粒子小球将产生与光束的动量变化大小相等、方向相反的动量。又根据牛顿第二定律可知,粒子小球受到的作用力就等于这一动量变化率,即 FA。
1.2.3梯度力
这种由于光场强度分布不均匀而产生的力,称为梯度力(Gradient Force),该力的大小正比于光的强度梯度,合力方向指向光束焦点。
1.2.4散射力
实际上当光穿过小球时,在小球表面会产生一定的反射,小球对光也有一定的吸收,这都将施加一推力于小球,此力称为散射力(Scattering Force),它正比于辐射强度,方向指向光束传播方向 。1.2.5光阱形成
当焦点附近梯度力大于散射力时,则可以形成三维光学势阱而稳定地捕获微粒。光镊技术中的光阱主要就是依靠光梯度力形成的,其合力指向光束焦点,如图 3 所示。
1.3 阵列光镊的发展
1986年,A.Ashkin等成功地利用一束强会聚激光束实现了对生物微粒的三维捕获[3],并可在基本不影响周围环境的情况下,对捕获物进行非接触性、无损伤活体的操作,即无机械损伤的遥控操作,自此基于激光的光镊技术诞生了。光镊技术已经被应用到了许多领域 。例如: 对生物微粒的操作、对马达分子进行皮牛量级力的测量、对双折射小球进行重排和旋转等[4]。
但单光镊每次仅能捕获一个微粒, 不能完成对大量微粒的同时捕获或操作, 因此自1998年开始出现了阵列光镊的概念, 它可同时对多个微粒进行三维捕获。2002年以来阵列光镊得到广泛关注, 出现了多种形成方式。例如, 利用声光偏转器( acousto-optics deflectors, AODs)、衍射光学元件( d iffract ive op tica l elements,DOE )、由计算机控制的空间光调制器( spat ia l lightmodulato rs, SLM) , 以及干涉、垂直腔面发射激光器( vertical cav ity surface em itt inglaser, VCSEL)、光纤、微透镜阵列等形成阵列光镊。阵列光镊可与其它微分析技术结合, 利用MEMS技术和微小激光器技术进行高度集成, 实现“ Lab-on-a-Chip”的设计理念[5]。
2 阵列光镊系统设计
本项目通过计算机控制SLM(空间光调制器)产生动态光阱阵列。液晶SLM包含许多由计算机控制的像素单元, 通过施加电场, 可以实时调整像素上液晶的取向, 从而产生相应的相移, 最终在光学捕获面上产生可实时控制光强分布的图案, 即一个平行激光束分成多个分开的部分,每一个光束通过会聚透镜聚焦形成一个光镊。其中每一个光点可以捕获一个微粒。
2.1 系统搭建
系统采用Hamamatsu X7550平行排列向列型空间光调制器对倍频Nd:YVO4(掺钕钒酸钇晶体)激光束进行重组以得到需要的多束激光[6][7]。每一束激光都经过一放大率为、数值孔径的卡尔蔡司S100TV油浸倒置光学显微镜头聚焦形成光阱。一块二向色分色镜将激光束反射到微粒上,同时允许被捕获的微粒的像通过到达CCD摄像头。通过使用放大率为的广角CCD摄像头,本系统可提供面积约为的观察区域。
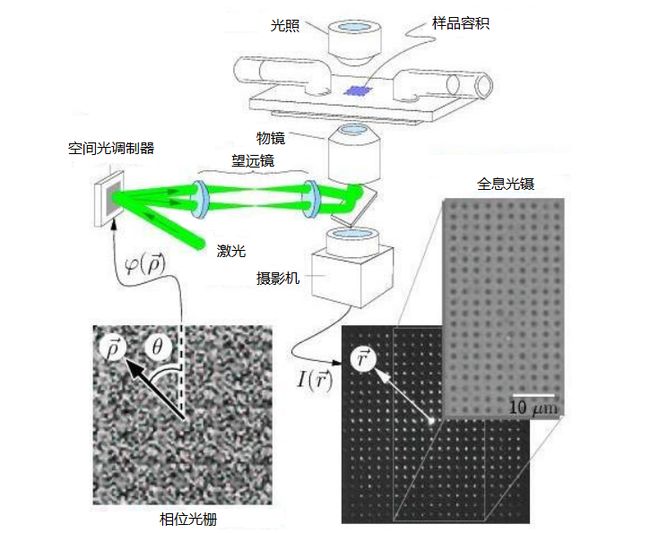
图4为利用反射式液晶空间光调制器生成全息阵列光镊系统的原理图。激光器发射的激光经准直后照射到SLM。计算机采用特定的算法, 调节SLM 上各像素点上的振幅和相位, 形成SLM 对入射光的调制, 经光学系统后生成阵列光束, 即用于捕获的阵列光阱。SLM的出现使得动态操控微粒变得很方便,阵列光镊的研究工作由此迅速展开。但该方法的缺陷是光能利用效率不高。由于需要经过调制重新分配输入光信息, 能量损耗比较大, 通常需用较大功率的光源才能产生足够强度的多光阱阵列。
Hamamatsu X7550平行排列向列型空间光调制器在其阵列上的每一个宽度为的像素都可以改变入射光的相位。控制软件提供的经校正的相位传递功能可在入射光波波长下提供从0—2π范围内150段不同的相位该变量。每一个像素改变的相位值都可以通过计算机软件界面单独调整,整块空间光调制器阵列的刷新率为5Hz。忽略SLM有限的空间带宽,可获得较复杂的捕获图样。
图4中400个可操控的光阱是可达到的最大数量。嵌入的相位光栅占的全息图像的1/25,形成20*20的光阱。白色区域对应于2π的相位变化,黑色对应于0。然后通过望远镜和大数值孔径物镜将它们聚焦成光阱。样品放在石英流动池里,通过传统微观摄像装置即可获取图像。内置的摄像显微照片表明从样品平面反射回来光光强I(r)。更小的内部照片显示了运动的光阱,操控着200胶质聚苯乙烯小球,直接大约为800nm。
2.2全息光镊系统原理
调制入射光的相位而非振幅足以获得聚焦在物点形成光阱的任意强度图样。这种强度变化型相位光栅通常被称为开诺全息图。
调制入射光先从电场![]() 分量开始,设DOE面相位固定,即
分量开始,设DOE面相位固定,即![]() ,单位强度为1,即
,单位强度为1,即![]() 。DOE的数值孔径Ω中的位置由
。DOE的数值孔径Ω中的位置由![]() 决定。
决定。![]() 为入射光的实振幅特性,为了表述清晰,忽略入射光的偏振化方向。则DOE会在入射光波阵面上附加一个相移
为入射光的实振幅特性,为了表述清晰,忽略入射光的偏振化方向。则DOE会在入射光波阵面上附加一个相移![]() ,最终调制得到需要的出射光图样。每一个光阱的电场分量
,最终调制得到需要的出射光图样。每一个光阱的电场分量![]() 与DOE面上的电场分量
与DOE面上的电场分量![]() 有关,其关系为一广义傅里叶变换[8]:
有关,其关系为一广义傅里叶变换[8]:

式中,![]() 为包括准直透镜和物镜在内的光学系统有效焦距。
为包括准直透镜和物镜在内的光学系统有效焦距。![]() 可被用作第j个光阱的转换,
可被用作第j个光阱的转换,![]() 为它的逆。对通常的光镊聚焦面来说,
为它的逆。对通常的光镊聚焦面来说,![]() 。
。
若计算出来的激光振幅![]() 等于捕获光的振幅
等于捕获光的振幅![]() ,则
,则![]() 就是需要的捕获光图样的开诺全息图。遗憾的是,这通常是不能实现的。更普遍的是振幅
就是需要的捕获光图样的开诺全息图。遗憾的是,这通常是不能实现的。更普遍的是振幅![]() 随着光线偏离理想的捕获光
随着光线偏离理想的捕获光![]() 而发生变化,产生鬼像和其他像差。尽管如此,忽略这些缺点,将开诺全息图结合式(1)仍然可以产生实用的捕获图样。将式(1)和式(2)与开诺全息图反复迭代则能产生更好且更据普遍性的结果。
而发生变化,产生鬼像和其他像差。尽管如此,忽略这些缺点,将开诺全息图结合式(1)仍然可以产生实用的捕获图样。将式(1)和式(2)与开诺全息图反复迭代则能产生更好且更据普遍性的结果。
根据Gerchberg and Saxton (GS)的研究,将式(1)和式(2)中的相位因子![]() 简化为
简化为![]() 以获得想要的开诺全息图并用来计算在捕获光位置上实际的光束特性
以获得想要的开诺全息图并用来计算在捕获光位置上实际的光束特性![]() :
:
经典GS算法将 简化为目标振幅
简化为目标振幅![]() ,相应的相位
,相应的相位![]() 不变,使用式(1)和式(2)对下一个简化相位
不变,使用式(1)和式(2)对下一个简化相位 求解。分数
求解。分数 表示第n次近似后入射光实际传递到光阱中的功率,这对追踪算法中聚焦位置有帮助。
表示第n次近似后入射光实际传递到光阱中的功率,这对追踪算法中聚焦位置有帮助。
对本系统来说,简化GS算法得到了一个慢速非单调聚焦[9]。此外,还发现了另一个简化公式:
当![]() 时可得到快速单调的聚焦。由此导出的简化
时可得到快速单调的聚焦。由此导出的简化![]() 可以被离散化,并传输到SLM上产生捕获图样。在SLM只能提供明显可变的离散相移量时,离散化可结合到每次迭代中以最小化相关的误差。在以下所有例子中,这套算法在捕获光初始相位
可以被离散化,并传输到SLM上产生捕获图样。在SLM只能提供明显可变的离散相移量时,离散化可结合到每次迭代中以最小化相关的误差。在以下所有例子中,这套算法在捕获光初始相位![]() 。
。
随机的情况下,经过2-3次迭代后产生的开诺全息图可达到理论效率的80%,且常可达到大于90%的效率。对式(2)和式(3)的迭代优化是理论上的效率,因为离散变化仅在实际捕获位置上可被计算。

图2:用动态全息光镊将直径0.99um的26个硅土小球组成的五边形图案转变成圆。
(a)原始图案(b)16步之后(c)38步之后的最终图像。
图2(a)显示26个直径为0.99微米的硅胶球悬浮在水中,并陷入一个由光镊制造(见公式2-3)而成的二维五角形模型。通过调整相位而将光阱移动到另一个位置,进而改变一系列光阱位置从那个人形成新的形状变换开诺衍射的位置使微粒到达另外一个位置从而达到移动球体。进行一系列新的设置从而形成一个新的图形。图2(b)显示了相同的16个这样的球体组成的的啤酒花,图2(c)是38个。用1mW的光驱动每个光阱以保持粒子被困时的热稳定性。增加捕获功率至10mV并将捕获模式提高至每步2um,我们将能以最高10um/s的速度移动粒子。
与平面运动相比也可以实现通过一系列离散的位置快速扫描一个光镊,从而创建一个分时捕获模式。连续照明全息光阱提供了几个优势。然而,全息光镊模式可以更广泛的定时分布空间光阱的数量并检索捕获每个粒子。此外,被不断照亮的光阱需要有较低的峰值强度,以减少对敏感样品的损害。
类似的重组也可能与先前的动态全息光镊实现[10]。这些研究使用快速傅里叶转换在整个捕获平面优化预测强度。经常达到理论效率超过95%,然而,这里被采用的离散转换可使我们编码更多适用的光阱模式。
2.3全息三维光镊
动态全息光镊不仅限于平面结构。如果激光束照射到SLM略有偏离,整个光阱的模式将集中于下游的焦平面。这样的偏移可以被菲涅耳透镜所引导,编码为一个相位光栅:
其中z是一个有效焦距为f光学阵列中的光阱相对于焦平面的距离,比起把一个单独的菲涅耳透镜放进输入光束中,通过对现有的全息图像添加透镜的相位调制,也可以获得相同的功能:![]() 。
。
图3(a)显示了一个以这种方式完成的典型的阵列光镊整体位移的平面。在我们的系统中,面外移动的范围大约是±10um。
单独的镜头功能可以分别应用于每个光阱焦点程序,而不是应用于整个捕获模式,在方程(1)和(3)、图3(b)显示小球们被通过这种方式的多个平面所独立移动。

图3三维运动与全息光镊。
(a)中的图像显示3-4硅球,直径0.99微米,被困在一个平面上,利用EQ5移动±5微米。球体的图像变化,因为他们相对于焦平面移动。(b)七个球体被困住,同时通过七种不同的平面使用开诺全息计算:公式(6)
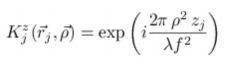 (6)
(6)
其他的相位修改可实现额外的功能。例如,相位特性
![]() (7)
(7)
将一个普通高斯激光束转化为Laguerre-Gaussian(拉盖尔-高斯)模式(15),其相应的光学镊子形成所谓的光学涡旋(16)、(17);(18)。这里的是 DOE的极坐标平面(见图1),是光束的拓扑电荷(15)。
因为所有相位存在沿圆周Laguerre-Gaussian光束,沿其强度轴取消光束的相消干涉,所有的焦点。光学旋涡因此出现明亮的环周围的黑暗的中心。这样的黑暗陷阱诱捕反射被证明是有用的,吸收(19)低介电粒子(18),同时不兼容常见的光学镊子。
将![]() 加进全息图像,编码光镊产生了一个数组的数组相同的光学旋涡,如图4(a)所示。这里,光阱阵列被放置在显微镜焦平面的镜子所反射。漩涡形成相位函数也可以应用于单独的陷阱。
加进全息图像,编码光镊产生了一个数组的数组相同的光学旋涡,如图4(a)所示。这里,光阱阵列被放置在显微镜焦平面的镜子所反射。漩涡形成相位函数也可以应用于单独的陷阱。
混合阵列光镊和光学旋涡的演示如图4(b)所示。
图4 (a)三角形阵列的光学涡旋的拓扑电荷l = 20从一个等价的创建数组光镊通过公式(7)。
光聚焦光漩涡是由从镜子反射成像示例平面。一个漩涡的插图显示了一个更详细的视图的结构。(b)混合阵列光镊(l=0)和在相同的配置上l=15和l=30的光学旋涡(a),同公式(8)计算.光阱的振幅均匀亮度的调整。(c)胶体聚苯乙烯微球直径800纳米困在一系列l=15光学旋涡的3*3方形区域。
先前的报道[11]光学涡旋捕获被认为是LaguerreGaussian模式和相对较小的拓扑命令![]() 。图(b)4中的示例了
。图(b)4中的示例了![]() 因此迄今被报道的最强烈的光学旋涡和
因此迄今被报道的最强烈的光学旋涡和![]() 的光阱在当前系统很容易创建。
的光阱在当前系统很容易创建。
图4(c)显示多个胶粒被困在![]() 漩涡3x3的阵列的明亮圆周内。因为LaguerreGaussian模式拥有螺旋型的波阵面,粒子受切向力困在光漩涡。光学旋涡是有用的,因此,在小尺度为驱动,例如在微机电系统(MEMS)。多个粒子被困在阵列的光学涡旋有良好的协同行为,这将在其他地方再讨论。
漩涡3x3的阵列的明亮圆周内。因为LaguerreGaussian模式拥有螺旋型的波阵面,粒子受切向力困在光漩涡。光学旋涡是有用的,因此,在小尺度为驱动,例如在微机电系统(MEMS)。多个粒子被困在阵列的光学涡旋有良好的协同行为,这将在其他地方再讨论。
漩涡形成(vortex-forming)内核![]() 可与
可与![]() 结合产生三维阵列的漩涡。这种异构捕获模式对组织不同的材料分层三维结构和在扩展的动力系统上的力量与扭矩施加控制是有效的。目前的研究演示了一个高斯激光束可以如何被修改来创建三维阵列光镊和光学旋涡,因为任何模式的光有潜在的应用,所以其他归纳效仿也是轻而易举的。例如,锥透镜相位剖面
结合产生三维阵列的漩涡。这种异构捕获模式对组织不同的材料分层三维结构和在扩展的动力系统上的力量与扭矩施加控制是有效的。目前的研究演示了一个高斯激光束可以如何被修改来创建三维阵列光镊和光学旋涡,因为任何模式的光有潜在的应用,所以其他归纳效仿也是轻而易举的。例如,锥透镜相位剖面![]() 创建了一个近似的贝塞尔模式,其集中到长度由
创建了一个近似的贝塞尔模式,其集中到长度由![]() 控制的轴线光阱,更好的轴线光阱来源于更精确模式样板(mode-former)
控制的轴线光阱,更好的轴线光阱来源于更精确模式样板(mode-former)![]() ,其中R是在SLM平面上的有效孔径半径。这些和其他广义捕获模式将在别处讨论。光学旋涡和常规光镊的线性组合可以作为光学瓶和控制旋转器。所有这些捕获模式可以使用上面描述的技术动态组合。
,其中R是在SLM平面上的有效孔径半径。这些和其他广义捕获模式将在别处讨论。光学旋涡和常规光镊的线性组合可以作为光学瓶和控制旋转器。所有这些捕获模式可以使用上面描述的技术动态组合。
捕获模式的复杂性在实践中被维持每一个光阱的三维强度梯度的需要,和可以在SLM准确编码的最大信息内容所限制。例如,前者考虑排除了形成一个三维立方光镊阵列与晶格常数小于10um,而后者限制我们的光学旋涡在![]() 。
。
在这些范围内,动态全息光镊可被高度配置,操作无创在开放和封闭的环境中,并且可以加上计算机视觉技术来创建完全自动化的系统。单个装置从而可以适应范围广泛的应用而程序无需修改。动态全息光镊应该有大量的生物技术应用,包括大规模并行高通量筛选、亚细胞工程和高分子排序。在材料科学、材料组织成层次三维结构的能力构成了一种全新的制造技术。作为研究工具,动态全息光镊将光镊的证明效用与前所未有的灵活性和适应性。
3 参考文献
[1]A. Ashkin. “History of optical trapping and manipulation of small-neutral particle, atoms, and molecules.”IEEE J. Sel. Top. Quantum Elec.6, 841–856 (2000).
[2] D. G. Grier. “Optical tweezers in colloid and interface science.”Cur. Opin. Colloid Interface Sci.2, 264–270 (1997).
[3]E. R. Dufresne and D. G. Grier. “Optical tweezer arrays and optical substrates created with diffractive optical elements.”Rev. Sci. Instrum.69, 1974–1977 (1998).
[4]D. G. Grier and E. R. Dufresne. “Apparatus for applying optical gradient forces.” U. S. Patent 6,055,106, The University of Chicago (2000).
[5] E. R. Dufresne, G. C. Spalding, M. T. Dearing, S. A. Sheets and D. G. Grier“Computer-generated holographic optical tweezer arrays.”Rev. Sci. Instrum.72, 1810–1816 (2001).
[6]Jennifer E. Curtis,Brian A. KossDavid G. GrierDynamic .Holographic Optical Tweezers. Opt. Commun. 207, 169-175 (2002)
[7]Jennifer E. Curtis David G. Grier.Structure of Optical Vortices Phys. Rev. Lett. 90, 133901 (2003)
[8] 孙晴,任煜轩,姚焜,李银妹,卢荣德.阵列光镊衍射元件的算法设计. 《中国激光》 (2011)
[9]J. Arlt, V. Garcés-Chávez, W. Sibbett and K. Dholakia. “Optical micromanipulation using a Bessel light beam.”Opt. Commun.197, 239–245 (2001).
[10] J. Arlt and M. J. Padgett. “Generation of a beam with a dark focus surrounded by regions of higher intensity: The optical bottle beam.”Opt. Lett.25, 191–193 (2000).
[11] L. Paterson, M. P. MacDonald, J. Arlt, W. Sibbett, P. E. Bryant and K. Dholakia. ``Controlled rotation of optically trapped microscopic particles.”Science292, 912–914 (2001).