奇异值分解的反变换matlab程序,奇异值分解(SVD)基础概念及MATLAB仿真
奇异值分解(SVD)基础概念及MATLAB仿真
奇异值分解(SVD)基础概念及MATLAB仿真
奇异值分解(singular value decomposition,简称SVD)不仅广泛应用于机器学习领域,也在控制理论中有着广泛的应用。本文主要介绍SVD的基本原理。
文章目录
一、预备知识
1.1 特征值与特征向量
1.2 幺正矩阵(酉矩阵)(Unitary Matrix)
酉矩阵的性质:
1.3 特征分解
二、SVD定义
2.1 求矩阵V
2.2 求矩阵U
2.3 求矩阵Σ
三、SVD计算举例
四、MATLAB仿真训练
五、SVD优势
六、小结
1.1 特征值与特征向量
设 A 是n阶方阵,如果存在数λ和非零n维列向量 x,使得 Aα=λα 成立,则称 λ 是矩阵A的一个特征值(characteristic value),而α是矩阵A对应于特征值λ的特征向量(Eigenvector)。
1.2 幺正矩阵(酉矩阵)(Unitary Matrix)
泛泛来讲,如果一个n阶方阵,它的列向量构成一组标准正交基,那么这个矩阵就是幺正矩阵,或称酉矩阵。
一个简单的充分必要判别准则是:方阵U的共扼转置乘以U等于单位阵,则U是酉矩阵。即酉矩阵的逆矩阵与其伴随矩阵相等。
对于实数矩阵而言,共轭转置等于其转置。
酉矩阵的性质:
① 矩阵U为酉矩阵的充要条件是它的共轭转置矩阵等于其逆矩阵,
即
U
?
=
U
?
1
U^{*}=U^{-1}
U?=U?1 或
U
?
U
=
U
U
?
=
I
U^{*}U=UU^{*}=I
U?U=UU?=I
② 若酉矩阵的元素全是实数,则其为正交矩阵;
正交矩阵的性质:转置等于伴随,即
U
T
=
U
?
U^{T}=U^{*}
UT=U?
③ 酉矩阵的行列式的绝对值为1;
④ U=VΣV*
其中V是酉矩阵,Σ 是主对角线上元素绝对值为1的对角阵。
在查找相关文献时,遇到了一个问题:共轭转置矩阵与伴随矩阵为什么都用A*表示?
关于详细解答,请参考:https://zhuanlan.zhihu.com/p/87330558
这里只总结一句:当A为酉矩阵时,伴随矩阵等于其共轭转置矩阵。
1.3 特征分解
求出特征值和特征向量之后,就可以对方阵A进行特征分解。
A
=
W
Σ
W
?
1
A=WΣW^{-1}
A=WΣW?1
其中W是这n个特征向量所张成的n x n维酉矩阵(
W
T
=
W
?
1
W^{T}=W^{-1}
WT=W?1)。
因此也可以写成:
A
=
W
Σ
W
T
A=WΣW^{T}
A=WΣWT
【注意】:要进行特征分解,矩阵A必须是方阵。如果A不是方阵,即行和列不相同时,就不能用这种方法对矩阵进行分解,由此引入SVD的概念。
SVD也是对矩阵进行分解,但是与特征分解不同,SVD并不要求分解的矩阵为方阵。
定义矩阵A的SVD为:
A
=
U
Σ
V
T
A=UΣV^{T}
A=UΣVT
其中U是一个m x m的矩阵,Σ是一个m x n的矩阵,除了对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值,V是一个n x n的矩阵。U和V都是酉矩阵,即满足
U
T
U
=
I
U^{T}U=I
UTU=I,
V
T
V
=
I
V^{T}V=I
VTV=I
那么我们如何求出SVD分解后的U,Σ,V这三个矩阵呢?
2.1 求矩阵V
将矩阵A的转置与A作矩阵乘法,得到一个n x n的方阵
A
T
A
A^{T}A
ATA。由于
A
T
A
A^{T}A
ATA是方阵,因此可以进行特征分解,而且得到特征值λi与特征向量vi。将该方阵的所有特征向量张成一个n x n的矩阵V,这就是SVD中的矩阵V了。
一般,将V中的每个特征向量叫做A的右特征向量。
2.2 求矩阵U
相反,将矩阵A与A的转置作矩阵乘法,得到一个m x m的方阵
A
A
T
AA^{T}
AAT。由于
A
A
T
AA^{T}
AAT是方阵,因此可以进行特征分解,而且得到特征值λi与特征向量ui。将该方阵的所有特征向量张成一个n x n的矩阵U,这就是SVD中的矩阵U了。
一般,将U中的每个特征向量叫做A的左特征向量。
2.3 求矩阵Σ
A
=
U
Σ
V
T
?
A
V
=
U
Σ
V
T
V
?
A
V
=
U
Σ
?
A
v
i
=
σ
i
u
i
?
σ
i
=
A
v
i
/
u
i
A=UΣV^{T} ? AV=UΣV^{T}V ? AV=UΣ ?Av_i=σ_iu_i?σ_i=Av_i/u_i
A=UΣVT?AV=UΣVTV?AV=UΣ?Avi?=σi?ui??σi?=Avi?/ui?
或
A
=
λ
1
u
1
(
v
1
)
T
+
λ
2
u
2
(
v
2
)
T
+
.
.
.
A=λ_1u_1(v_1)^T+λ_2u_2(v_2)^T+...
A=λ1?u1?(v1?)T+λ2?u2?(v2?)T+...
通过上式就可以求出每个奇异值σi,进而求出奇异值矩阵Σ。
【证明】:
因为:
U
T
U
=
I
U^{T}U=I
UTU=I,
Σ
T
Σ
=
Σ
2
Σ^{T}Σ=Σ^2
ΣTΣ=Σ2
故
A
=
U
Σ
V
T
?
A
T
=
V
Σ
T
U
T
?
A
T
A
=
V
Σ
T
U
T
U
Σ
V
T
=
V
Σ
2
V
T
A=UΣV^{T} ? AT=VΣ^{T}U^{T} ? A^TA=VΣ^TU^TUΣV^T=VΣ^2V^T
A=UΣVT?AT=VΣTUT?ATA=VΣTUTUΣVT=VΣ2VT
由此可以看出,ATA的特征向量组成的的确是V矩阵,同理也可证明U矩阵。
同时,我们发现,特征值矩阵等于奇异值矩阵的平方,也可以说:
σ
i
=
λ
i
σ_i=\sqrt{λ_i}
σi?=λi?
?
这也是一个十分有用的公式。
例:求矩阵A=
(
1
0
0
2
0
0
)
\left( \begin{array}{lcr} 1 & 0 & 0 \\ 2 & 0 & 0 \end{array} \right)
(12?00?00?) 的奇异值分解。
解:我们首先求出ATA和AAT:
A
T
A
=
(
1
2
0
0
0
0
)
(
1
0
0
2
0
0
)
=
(
5
0
0
0
0
0
0
0
0
)
A^TA=\left( \begin{array}{lcr} 1 & 2 \\ 0 & 0 \\ 0 & 0 \end{array} \right) \left( \begin{array}{lcr} 1 & 0 & 0 \\ 2 & 0 & 0 \end{array} \right)= \left( \begin{array}{lcr} 5 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)
ATA=???100?200????(12?00?00?)=???500?000?000????,
A
A
T
=
(
1
0
0
2
0
0
)
(
1
2
0
0
0
0
)
=
(
1
2
2
4
)
AA^T= \left( \begin{array}{lcr} 1 & 0 & 0 \\ 2 & 0 & 0 \end{array} \right) \left( \begin{array}{lcr} 1 & 2 \\ 0 & 0 \\ 0 & 0 \end{array} \right)= \left( \begin{array}{lcr} 1 & 2 \\ 2 & 4 \\ \end{array} \right)
AAT=(12?00?00?)???100?200????=(12?24?),
根据特征值:λ1=5,λ2=λ3=0对应的特征向量为:
v1=[1,0,0]T,v2=[0,1,0]T,v3=[0,0,1]T
从而
V
=
(
1
0
0
0
1
0
0
0
1
)
V=\left( \begin{array}{lcr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)
V=???100?010?001????,
根据特征值:λ1=5,λ2=0对应的特征向量为:
u1=[
1
/
5
,
2
/
5
1/\sqrt5,2/\sqrt5
1/5
?,2/5
?]T,u2=[
?
2
/
5
,
1
/
5
-2/\sqrt5,1/\sqrt5
?2/5
?,1/5
?]T
从而
U
=
(
1
/
5
?
2
/
5
2
/
5
1
/
5
)
U=\left( \begin{array}{lcr} 1/\sqrt5 & -2/\sqrt5 \\ 2/\sqrt5 & 1/\sqrt5 \\ \end{array} \right)
U=(1/5
?2/5
???2/5
?1/5
??)。
根据非零特征值λ1=5,则A的奇异值为σ1=
5
\sqrt5
5
?,故D=
5
\sqrt5
5
?。
最终得到A的奇异值分解:
A
=
U
Σ
V
T
=
U
(
5
0
0
0
0
0
)
V
T
=
(
1
/
5
?
2
/
5
2
/
5
1
/
5
)
(
5
0
0
0
0
0
)
(
1
0
0
0
1
0
0
0
1
)
A=UΣV^{T}=U\left( \begin{array}{lcr} \sqrt5 & 0 & 0\\ 0 & 0 & 0 \\ \end{array} \right)V^T= \left( \begin{array}{lcr} 1/\sqrt5 & -2/\sqrt5 \\ 2/\sqrt5 & 1/\sqrt5 \\ \end{array} \right)\left( \begin{array}{lcr} \sqrt5 & 0 & 0\\ 0 & 0 & 0 \\ \end{array} \right) \left( \begin{array}{lcr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right)
A=UΣVT=U(5
?0?00?00?)VT=(1/5
?2/5
???2/5
?1/5
??)(5
?0?00?00?)???100?010?001????
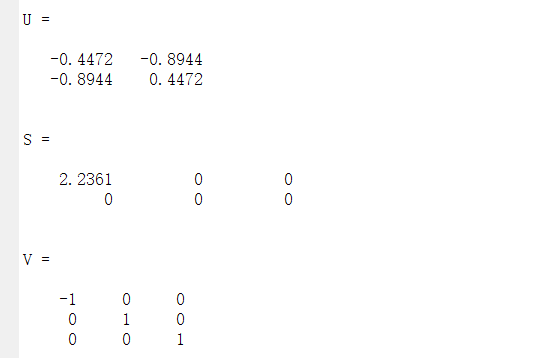
MATLAB提供了svd函数用于奇异值分解,其代码如下:
A=[1,0,0;2,0,0];
[U,S,V]=svd(A)
输出结果:
SVD为什么值得这么关注呢?
我们来看一个引例:
奇异值分解可用于高效地表示数据。例如,假设我们希望传输以下图像,该图像由15个25个黑色或白色像素的阵列组成。
由于该图像中只有三种类型的列,如下所示,因此应该可以以更紧凑的形式表示数据。
这样就大大减少了要记录的数据数量。
SVD作为一个很基本的算法,在机器学习和控制理论等领域有着广泛的应用。
当然,SVD的缺点是分解出的矩阵解释性往往不强,有点黑盒子的味道,不过这不影响它的使用。
参考:http://www.ams.org/publicoutreach/feature-column/fcarc-svd
奇异值分解(SVD)基础概念及MATLAB仿真相关教程
蓝桥秘密冲刺计划(9.26)数的分解
蓝桥秘密冲刺计划(9.26)数的分解 定位:2019年第十届蓝桥杯省赛C/C++ B组试题D 原题: 属性:枚举 难度:破壳 独白: 相比20年的试题D这题简直不知道简单了几倍。 较为简单的模拟题,只需要循环枚举就可以了,当然最好在模拟判断的时候,添加一个功能函数来
C语言 strtok函数分解字符串为一组字符串
C语言 strtok函数分解字符串为一组字符串 C语言 strtok函数分解字符串为一组字符串 一、SYNOPSIS #include string.h char *strtok(char *str, const char *delim); 二、DESCRIPTION The strtok() function breaks a string into a sequence of zero or more n
矩阵奇异值分解及伪逆
矩阵奇异值分解及伪逆 矩阵A的奇异值分解 矩阵A的伪逆 python计算矩阵的奇异值分解和伪逆 a = np.matrix([[2, -1, 0],[4,3,-2]])u, s, vt = np.linalg.svd(a, full_matrices=True)np.linalg.pinv(a) Computing SVD and pseudoinverse
【动手学MVG】矩阵分解与线性方程组的关系,求解线性方程组实战
【动手学MVG】矩阵分解与线性方程组的关系,求解线性方程组实战代码 文章目录 本文解决的问题 QR分解 投影矩阵分解得到内外参 SVD分解 最小二乘问题 最小二乘问题的求解方法 (列)满秩最小二乘问题 正规化方法 QR分解方法 SVD 分解方法 亏秩最小二乘问题 齐次
最长树链 ( dfs + 质因数分解 )
最长树链 ( dfs + 质因数分解 ) 题目链接 解题报告: 我们不妨枚举最长树链 gcdgcdgcd , 那么该条树链上所有的点的权值可表示成 k?gcdk*gcdk?gcd 同样也可表示成 k?gcd′(gcdk*gcd'(gcdk?gcd′(gcd%gcd′==0)gcd'==0)gcd′==0) ,因此我们可以用质因子对这些点
Pairs Forming LCM LightOJ - 1236 唯一分解+组合数(数论专题)
Pairs Forming LCM LightOJ - 1236 唯一分解+组合数(数论专题) Find the result of the following code: long long pairsFormLCM( int n ) { long long res = 0; for( int i = 1; i = n; i++ ) for( int j = i; j = n; j++ ) if( lcm(i, j) == n ) res++; /
手把手教你 javap 反编译分解代码,授人以鱼不如授人以渔
手把手教你 javap 反编译分解代码,授人以鱼不如授人以渔 Class文件结构 Class魔数和版本 常量池 访问标志 类索引、父类索引与接口索引集合 字段表集合 字段访问标志 方法表集合 属性表集合 属性表之异常表 我之前写了一篇关于class文件重要性的,并且从宏观
具象业务需求再抽象分解——系统设计
具象业务需求再抽象分解——系统设计 经过前篇需求梳理,商场停车收费业务需求情况已经十分明了,本节就依据前文的输出做为输入,开始系统设计工作,包括功能模块设计、存储设计、架构设计等,为后面的编码提供良好的基础保障。 有同学可能会有疑问,都使用敏