自适应滤波器更新算法-EP3

续接上一篇博文，继续介绍博主阅读论文总结的几种优化后的自适应滤波器更新算法!

1、PNLMS和IPNLMS算法

  在介绍接下来的改进自适应滤波算法之前，需要先介绍一下PNLMS和IPNLMS算法，因为之后的算法是基于这两种算法之上进行改进的。

1.1 算法原理

  在回声消除的应用中，实际回声路径的脉冲响应与所处房间的大小、墙壁的材料、麦克风的位置、环境温度等息息相关。在回声路径具有长脉冲响应的情况下，则需要上千阶的自适应滤波器以用于逼近回声路径脉冲响应，而回声脉冲响应具有稀疏特性，其系数绝对值只在短时间内大于零，其余则无限趋近于零。上千阶的滤波器系数中实则只有几百个发挥实际作用，且决定着回声路径估计的准确性。基本的LMS和NLMS算法收敛速度一般不能达到要求，在此背景下，(Proportionate Normalized Least Mean Square, PNLMS)算法被提出。

  PNLMS 算法的基本思想是保证有用的滤波器系数具有较大的收敛因子，而其余不发挥作用和作用很小的滤波器系数仍保留小的收敛因子。滤波器权值更新公式可表示为：
$$w(n+1)=w(n)+\frac{\mu G(n+1)}{\delta +x^T(n)G(n+1)x(n)}e(n)x(n)$$
式中 $G(n)$ 为N维的对角增益矩阵，以对滤波器各权值系数分配步长权重，表示为：
$$G(n+1)=diag\{g_1(n+1),g_2(n+1),...,g_N(n+1)\}$$
其中，
$$g_k(n+1)=\frac{{\gamma }_k(n+1)}{\frac{1}{N}{\sum }_{i=1}^N{\gamma }_i(n+1)}$$
且$1\le k\le N$，式中的
$${\gamma }_k(n+1)=max\{\rho \ast max[{\delta }_p,|w_1(n)|,|w_2(n)|,...,|w_N(n)|],|w_k(n)|\}$$
  ${\delta }_p$ 为在滤波器初始阶段调整更新参数的因子，$\rho$ 的取值将影响算法的整体收敛速度，较大的 $\rho$ 会使得收敛速度减缓，但也不宜取值过小，一般取 $5/M$。当 $\rho =1$ 时，PNLMS算法将变为NLMS算法。

  PNLMS 算法的收敛速度提升是以回声路径脉冲响应具有高稀疏程度为前提条件的，因此在一些低稀疏度的场景下，其效果甚至没有 NLMS 算法表现好，且随着迭代的进一步进行，其收敛速度会发生显著减缓的情况。为了结合 PNLMS 和 NLMS 算法的优势， IPNLMS 算法在二者的基础上采取了可调整算法比重的参数 $\theta$：
$$g_k(n+1)=\frac{1-\theta }{2}+(1+\theta )\frac{N|w_k(n)|}{2||w(n)||+\epsilon }$$
  其中$1\le k\le N$，$\epsilon$ 为一个小的正常数，式中 $||w(n)||={\sum }_{k=1}^N|w_k(n)|$。则上式针对$g_k(n+1)$ 运算的右半部分第一项可以看成是 IPNLMS 算法的 NLMS 成分，而第二项可以是PNLMS的成分。当 $\theta =1$ 时 IPNLMS 算法退化为 PNLMS 算法，当 $\theta =-1$时 IPNLMS 算法退化为 NLMS 算法[26]。

2.2 算法分析

function [e,y, w] = PNLMS(d, x, M, aplha, beta)
    % 输入:
    % d  - 麦克风语音
    % x  - 远端语音
    % a  - 偏置参数
    % M  - 滤波器阶数
    % ppp - 5/M为正常数
    
    % 输出:
    % e - 近端语音估计
    % y - 远端回声估计
    % w - 滤波器参数
    d_length = length(d);
    if (d_length <= M)
        print('error: 信号长度小于滤波器阶数！');
        return; 
    end
    if (d_length ~= length(x))  
        print('error: 输入信号和参考信号长度不同！');
        return; 
    end

    ppp = 5/M;
    xx = zeros(M,1);
    rx = zeros(M,1);
    w1 = zeros(M,1);        % 滤波器权重
    y = zeros(d_length,1);   % 近端语音
    e = zeros(d_length,1);  % 误差
    G=eye(M);     %N维对角增益矩阵
    sum = 0;
    for n = 1:d_length
        %在输入信号x前补上M-1个0，使输出y与输入具有相同长度
        for zz = 1:M
            rmax =max(0.01,ppp*max(w1));%0.01为正常数
            rx(zz,:) = max(rmax,w1(zz,:));
            sum= sum+rx(zz,:);
        end
        disp(sum)
        for zz = 1:M
           G(zz,zz) = rx(zz,:)/sum;
        end
        disp(G);
        xx = [xx(2:M);x(n)];    % (39,1)+(1,1)=(40,1)
        y(n) = w1' * xx;        % (40,1)'*(40,1)=1
        mu = aplha/(beta + xx'*G*xx);    % 步长
        e(n) = d(n) - y(n);     % 误差
        w1 = w1 + mu * G *e(n) * xx;
        w(:,n) = w1;
    end
end

上述为PNLMS算法的代码，IPNLMS算法的代码是在PNLMS算法的基础上做了一点改进，较为简单，这里就不再复现，留给同学们自己去学习了。

2.3 算法分析

• 上述的PNLMS算法解决了NLMS算法在回声脉冲响应具有稀疏特性情况下收敛速度过慢的问题，PNLMS 算法拥有初始收敛速度的优势，尤其在回声路径具有稀疏性条件下，其收敛速度则更加明显。
• 但是不是所有场景下，回声路径脉冲响应都具有高稀疏程度，因此在一些低稀疏场景下，PNLMS算法的效果甚至没有NLMS算法表现好，且随着迭代的进一步进行，其收敛速度会发生显著减缓的情况。
• IPNLMS算法就是结合了PNLMS和NLMS算法的优势，在二者的基础上采取了可调整算法比重的方式。由于调整算法比重参数的存在使得其内部两种算法的成分达到协调，因此使得其收敛速度保持在适中的状态。

2、一种改进的时变参数的比例自适应滤波算法

2.1 算法原理

  该算法由参考文献[1]提出，其是在IPNLMS算法的基础上进行进一步的优化。基本的 IPNLMS 算法，它是在 NLMS 算法和 PNLMS 算法之间采取了折中的处理思想，以规避各自的缺陷，但其内部可调整步长比重的参数 $\theta$ 设置为固定值，且此参数的取值直接决定着 IPNLMS 算法的性能是偏向于 NLMS 还是PNLMS。在回声路径的稀疏特性为已知的情况下，可以根据对应的稀疏度而采取适当的参数值。但在一般情况下，近似为未知系统内的回声路径脉冲响应的数值是先验未知的，因此其参数值的选取就无从依据。另一方面，若大的参数取值使得滤波器权值系数被按比例分配到较大的权值增量，此时自适应滤波器趋于收敛状态时，滤波器权值仍沿用此权值增量会使得 IPNLMS 算法出现不可避免的稳态失调，这在回声消除的应用中应尽量避免的。

  因此在参考文献[1]中，引入了变参数的算法思想，即让参数 $\theta$ 值能够随自适应滤波器工作状态而改变。在自适应滤波器开始工作时，采用大的 $\theta$ 值，此时 IPNLMS 算法性能将趋PNLMS，以提高初始的收敛速度，而在自适应滤波器最终达到收敛状态时，应使参数 $\theta$ 值不断调整变小并趋近于­1，使得 IPNLMS 算法此时的性能趋近于 NLMS 算法，以在最大程度上减少稳态失调的波动性。则针对$g_k(n+1)$ 运算变型为：
$$g_k(n+1)=\frac{1-\theta (n)}{2}+(1+\theta (n))\frac{N|w_k(n)|}{2||w(n)||+\epsilon }$$
其中，时变参数 $\theta (n)$ 的值域应被限制在$[-1,1]$ 之间。而 $\theta (n)$ 在文中计算为Sigmoid函数形式：
$$\theta (n)=\frac{2\phi +2}{1+e^{-\beta \ast x(n)}}-(\phi +2)$$
对于 $\theta (n)$ 的计算如何得出，可以去学习参考文献[1]，这里不过多介绍。

2.2 算法分析

  该算法主要是针对IPNLMS算法不足的地方进行优化，将固定值 $\theta$ 转换为函数，能够使其更具滤波器的工作状态进行动态调整，使得算法更具鲁棒性，能够应该更复杂的场景。但是 $\theta (n)$ 如何计算则变得尤为关键。这一点也值得我们学习并验证。

2.3 算法性能评价标准

2.3.1 均方误差(Mean Square Error, MSE)

  MSE 作为自适应滤波算法的通用评价标准，其表示式为：
$$MSE=10lo{g}_{10}E[e^2(n)]$$
  由上式可以看出，MSE 与误差信号 $e(n)$相关，MSE 曲线能够刻画自适应滤波器的误差信号不断变小的过程，也是其从迭代开始到逐渐收敛的过程，且 MSE 越值小，自适应滤波算法的性能就越优秀。

2.3.2 失调(Misalignment, MIS)

  MIS 从公式上解释又叫做权误差向量范数，其表示式为：
$$MIS=10lo{g}_{10}\frac{||h-w|{|}^2}{||h|{|}^2}$$
  式中 $h$ 即房间脉冲响应的真实值，$w$ 为自适应滤波器权值向量，$||.||$ 表示取 2­范数。在AEC 中，MIS 主要衡量的是使用的自适应滤波器不断调整权值，使其与目标值不断逼近而“学习”的过程。MIS 值越小，则自适应滤波器“学习”能力也越强，算法性能也就越好。

2.3.3 回声衰减系数(Echo Return Loss Enhancement, ERLE)

  ERLE 又叫回声返回损耗增益，是最为常用的一个指标，可以由下式计算：
$$ERLE=10lo{g}_{10}\frac{E[d^2(n)]}{E[e^2(n)]}$$
  作为 AEC 主要评价标准，ERLE 能够反映所采用的自适应滤波算法消除回声的能力。与MSE 的表示式对比可知，当期望信号 d(n)一定时，二者是互为相反的概念。因此，ERLE 值越大，则算法对回声的抑制能力也就越突出。

3、基于多带结构的改进型自适应滤波切换算法

3.1 算法原理

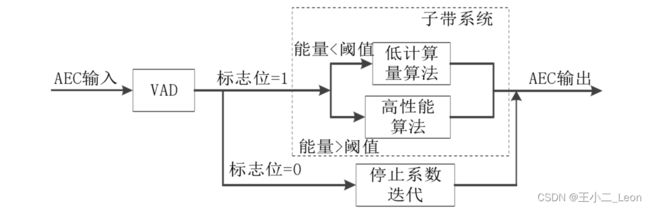
  该算法由参考文献[2]提出，即NLMS-NSAF算法。该算法的原理为，首先远端语音信号利用包络法判别有无语音段，然后将信号状态输出到自适应多带结构算法模块当中。若语音区输入信号的短时能量较大，则使用收敛速度快的自适应滤波算法；反之，若语音区输入信号的短时能量较小，需考虑计算量低的算法，当然，语音在无语音区时算法迭代停止。对输入语音信号能量高低的判定是通过和阈值 $T_s$ 比较得到的，可以理解为VAD检测。

  算法的整体原理图为：

该算法的具体实现步骤为：

第一步： 快慢包络 VAD 法判断语音状态。

第二步： 快慢包络法能够从 VAD 中提取出语音包络特性来进一步提高算法性能，参考文献[2]中提出了基于此检测方法的切换算法，即利用 VAD 分析值来切换抽头权重更新公式，以达到提高算法性能、降低运算量的目的。

第三步： 提出的切换 NLMS-NSAF 算法更新公式被写成如下式，式中的两个表达式都表示了权重矢量相对于上一次迭代的增加量，只是增加的幅度不同，而这个不同由第二步中的阈值决定，根据阈值与输入信号的能量做对比，选择不同的更新公式。

3.2 算法分析

• 在充分考虑语音特性的情况下，切换算法实现了算法在收敛速度的优势，同时完成了同算法复杂度的优化选择。最后达到了提高滤波算法性能、降低运算量的目的。
• 可以看出该算法滤波器的更新很大程度上会依赖VAD的结果，因此VAD对语音判别的准确性将会影响整个算法的效果，所以该算法无形之中又增加了影响算法效果好坏的因素。

4、 自适应算法的判断准则

  如何判断自适应算法是否为一种好的自适应算法，主要从以下几个点来判断：

• 收敛速度：它定义为算法在响应平稳输入时足够接近维纳最优解所需的迭代次数。快速收敛允许算法快速自适应于统计意义上未知的平稳环境。
• 失调(misaajustment)：这个参数提供了自适应滤波器集平均的最终均方误差与维纳滤波器所产生的最小均方误差之间偏离程度的—个定量测量。
• 跟踪(tracking)：当一个自适应滤波算法运行于非平稳环境时，该算法需要跟踪环境的统计量变化。然而算法跟踪性能受到两个相互矛盾的特性影响：收敛速度和由算法噪声引起的稳态波动。
• 鲁棒性(robustness)：对于—个鲁棒的自适应滤波器，小的扰动只会产生小的估计误差。
• 计算要求：计算要求包括：完成算法的一次完整迭代所需要的运算量(乘法和加法的次数)；存储数据和程序所需要的存储器位置的大小；在计算机上对算法编程所需要的投资。

参考文献

[1]严涛. 声学回声消除的自适应滤波方法研究[D].南京信息工程大学.

[2]魏丹丹. 声学回声消除中子带和块稀疏自适应算法研究[D]. 重庆邮电大学.

作者：王小二_Leon
欢迎任何形式的转载，但请务必注明出处。
限于本人水平，如果文章和代码有表述不当之处，还请不吝赐教。
本文章不做任何商业用途，仅作为自学所用，文章后面会有参考链接，我可能会复制原作者的话，如果介意，我会修改或者删除。

说明：对自适应滤波器算法的研究到此告一段落，由于博主能力有限，因此该篇中涉及到的算法代码都未复现，希望博主对各种算法的总结能够对自己和同学们有帮助，也欢迎各位指正！！！