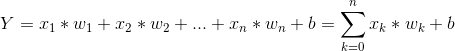python多元线性回归预测法,Python-Tensorflow2.3.0-多元线性回归预测(学习笔记)

Python-Tensorflow2.3.0-多元线性回归预测(学习笔记)

Python-Tensorflow2.3.0-多元线性回归预测(学习笔记)

编译器环境：win10-Anaconda3-python3.6-tensorflow2.3.0

预测数据下载地址：https://download.csdn.net/download/weixin_41788456/12902246

Tensorflow进行算法设计与训练的核心步骤：

目录

1.准备数据

2.构建模型

3.模型训练

4.模型预测

1.准备数据

多变量线性方程可以表达为

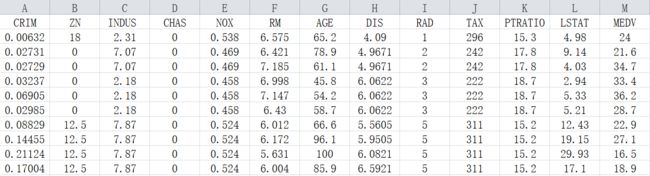
总共：506行*13列，其中506为样本数，前12列为样本特征，最后1列为样本标签

%matplotlib inline

import tensorflow as tf

import numpy as np

import matplotlib.pyplot as plt

import pandas as pd

from sklearn.utils import shuffle

//读取数据

df=pd.read_csv("E:/data/boston.csv",header=0)

print(df)

#获取df的值

df=df.values

#把df转换为np的数组格式

df=np.array(df)

#数据归一化

for i in range(12):

df[:,i]=df[:,i]/(df[:,i].max()-df[:,i].min())

x_data=df[:,0:12]

y_data=df[:,12]

2.构建模型

#定义特征数据和标签数据的占位符

tf.compat.v1.disable_eager_execution()

x=tf.compat.v1.placeholder(tf.float32,[None,12],name="X")#12个特征数据

y=tf.compat.v1.placeholder(tf.float32,[None,1],name="Y")#1个标签数据

print(x)

#定义一个命名空间

with tf.name_scope("model"):

#初始化值为shape=(12,1)的随机数

w=tf.Variable(tf.compat.v1.random_normal([12,1],stddev=0.01),name="W")

#初始化值为1.0

b=tf.Variable(1.0,name="b")

#w和x矩阵相乘，用matmul，mutiply为数乘

def model(x,w,b):

return tf.matmul(x,w)+b

#预测计算操作，前向计算节点

pred=model(x,w,b)

3.模型训练

#迭代次数

train_epochs=50

#学习率

learning_rate=0.01

#定义损失函数

with tf.name_scope("loss_Function"):

loss_function=tf.reduce_mean(tf.pow(y-pred,2))#均方差

#创建优化器

optimizer=tf.compat.v1.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

#声明会话

sess=tf.compat.v1.Session()

#定义初始化变量的操作

init=tf.compat.v1.global_variables_initializer()

#启动会话

sess.run(init)

loss_list=[]

#迭代训练

for epoch in range(train_epochs):

loss_sum=0.0

for xs,ys in zip(x_data,y_data):

xs=xs.reshape(1,12)

ys=ys.reshape(1,1)

_,loss=sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})

loss_sum=loss_sum+loss

#打乱数据顺序

xvalues,yvalues=shuffle(x_data,y_data)

b0temp=b.eval(session=sess)

w0temp=w.eval(session=sess)

loss_average=loss_sum/len(y_data)

loss_list.append(loss_average)

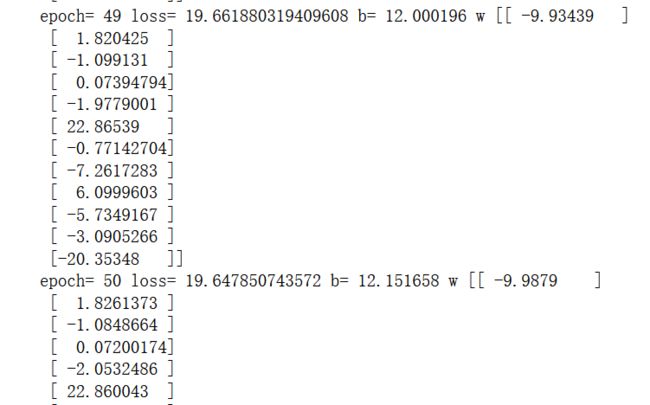
print("epoch=",epoch+1,"loss=",loss_average,"b=",b0temp,"w",w0temp)

输出结果：

损失函数收敛图：

4.模型预测

n=np.random.randint(506)

print(n)

x_test=x_data[n]

x_test=x_test.reshape(1,12)

predict=sess.run(pred,feed_dict={x:x_test})

print("预测值：%f"%predict)

target=y_data[n]

print("目标值：%f"%target)

预测结果：

301

预测值：23.178604

目标值：22.000000

Python-Tensorflow2.3.0-多元线性回归预测(学习笔记)相关教程

一元变量线性回归(房价预测) Python代码

一元变量线性回归(房价预测) Python代码 前言 本文主要内容是一元变量下的线性回归问题，给定2000~2013年的房价，预测2014年的房价。文中使用了梯度下降法和最小二乘法两种方法去求解。 一、训练数据 year price2000 2.02001 2.52002 2.92003 3.1472004 4.5

【线性回归模型】最小二乘法、lasso、岭回归、elastic net以及MA

【线性回归模型】最小二乘法、lasso、岭回归、elastic net以及MATLAB中lasso的使用 【线性回归模型】最小二乘法、lasso、岭回归、elastic net以及MATLAB中lasso的使用 1 问题描述 2 回归模型 3 MATLAB中lasso函数简单使用 4 画图展示拓扑重构结果 附录 吴恩达

【QBKbupt】第二章 线性表 C.线性表练习3

【QBKbupt】第二章 线性表 C.线性表练习3 #includebits/stdc++.husing namespace std;struct Node{int in;int cn;Node *next;};void init(Node **);void create(Node *,int);void calculate(Node *,Node *,Node *);void print(Node *);int main(){int n,m;Nod

【QBKbupt】第二章 线性表 B.线性表练习2

【QBKbupt】第二章 线性表 B.线性表练习2 #includebits/stdc++.husing namespace std;struct Node{int data;Node *next;};int main(){int n,x,y;char operate[10];Node head,*ptr,*ptr2;head.data =1;head.next=NULL;ptr=head;ptr2=head;scanf(%d,n);for(int

tensorflow 入门之五- 多变量线性回归

tensorflow 入门之五- 多变量线性回归 tensorflow 入门之五- 多变量线性回归 import tensorflow as tfimport matplotlib.pyplot as pltimport numpy as nptf.__version__ '1.14.0' # 加载数据boston=tf.contrib.learn.datasets.load_dataset('boston')x_train

保研复习——线性代数5相似矩阵

保研复习——线性代数5：相似矩阵 相似矩阵 1.方阵的特征值与特征向量 特征值与特征向量的定义 由(1)式可知，若λ 是矩阵A的特征值，α 为属于λ 的特征向量，则α 是齐次线性方程组(λE-A)x=0 的非零解。?|λE-A|=0 ，称|λE-A| 为矩阵A的 特征多项式 ，方

线性模型学习笔记

线性模型学习笔记 注：该文是根据开智学堂数据科学入门班的讲课内容整理而成，主讲人是肖凯老师。 线性模型 主要学习用 statsmodels 模块进行线性回归、逻辑回归和时间序列分析。 多个因素的定量化计算，是线性模型的最主要用途。 \[y=\beta_{0}+\beta_{1}x_{

无人驾驶轨迹跟踪仿真——线性时变模型预测代码详解

无人驾驶轨迹跟踪仿真——线性时变模型预测代码详解 无人驾驶轨迹跟踪仿真——线性时变模型预测代码详解 对照推导的公式，对代码进行一一详细注解，方便学习代码的同学。该代码为龚建伟《无人驾驶车辆模型预测控制》中第3章3.3.3的例子。 这一部分的推导过程