人工智能6-GA遗传算法
目录
一、遗传算法的简介
二、算法流程
三、参数经验设置
四、GA函数的实现
1.目标函数Griewank
2.目标函数Rastrigin
3.目标函数myfit(简单求解)
五、GA的优缺点
一、遗传算法的简介
遗传算法(Genetic Algorithm,GA)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法,是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法是从代表问题可能潜在的解集的一个种群开始的,而一个种群则由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现。
在遗传算法中,被优化的问题的解称为个体,它表示的是一个变量的一组序列,叫做基因串或者染色体。染色体通常被表达为简单的字符串或者数字串,也有其他的针对特殊的问题的采用的表示方法,这个过程称为编码。首先,算法会随机生成一定数量的个体,也可以人为地设定,这样可以提高初始种群的质量。在每一代中,所有的个体都被评价,并通过计算适应度函数得到一个适应度数值,依照适应度,对种群中的个体进行排序。然后,产生一个新的个体种群,也就是选择和繁殖,繁殖包括交配和突变。初始的数据便可以通过这样的选择原则组成一个相对优化的群体。之后,被选择的个体进入交配过程。
经过这一系列的过程(选择、交配和突变),产生的新一代个体不同于初始的一代,并一代一代向增加整体适应度的方向发展,因为最好的个体总是更多的被选择去产生下一代,而适应度低的个体逐渐被淘汰掉。过程不断重复:每个个体被评价,计算出适应度,两个个体交配,然后突变,产生第三代......直到满足终止条件为止。
二、算法流程
(1)初始化规模为 N的群体,其中染色体每个基因的值采用随机数产生器生成并满足问题定义的范围。当前进化代数Generation=0。
(2)采用评估函数对群体中所有染色体进行评价,分别计算每个染色体的适应值,保存适应值最大的染色体Best。
(3)采用轮盘赌选择算法对群体的染色体进行选择操作,产生规模同样为N的种群。
(4)按照概率Pc 从种群中选择染色体进行交配。每两个进行交配的父代染色体,交换部分基因,产生两个新的子代染色体,子代染色体取代父代染色体进入新种群。没有进行交配的染色体直接复制进入新种群。
(5)按照概率 Pm对新种群中染色体的基因进行变异操作。发生变异的基因数值发生改变。变异后的染色体取代原有染色体进入新群体,未发生变异的染色体直接讲入新群体。
(6)变异后的 新群体取代原有群体,重新计算群体中各个染色体的适应值。倘若群体的最大适应值大于Best的适应值,则以该最大适应值对应的染色体替代Best。
(7)当 前进化代数Generation加1。如果Generation超过规定的最大进化代数或Best达到规定的误差要求,算法结束;否则返回第(3)步。
三、参数经验设置
1.群体规模N
影响算法的搜索能力和运行效率。
若N设置较大,一次进化所覆盖的模式较多,可以保证群体的多样性,从而提高算法的搜索能力,但是由于群体中染色体的个数较多,势必增加算法的计算量,降低了算法的运行效率。
若N设置较小,虽然降低了计算量,但是同时降低了每次进化中群体包含更多较好染色体的能力。N的设置一般为20~100。
2.染色体的长度L
影响算法的计算量和交配变异操作的效果。
L的设置跟优化向题密切相关,一般由问题定义的解的形武和选择的编码方法决定;对于二进制编码方法,染色体的长度L根据解的取值范围和规定精度要求选择大小。
对于浮点数编码方法,染色体的长度L跟问题定义的解的维数D相同。
除了染色体长度一定的编码方法,Goldberg等人还提出了一种变长度染色体遗传算法Messy GA,其染色体的长度并不是固定的。
3.基因的取值范围R
R视采用的染色体编码方案而定。
对于二进制编码方法,R={0,1},而对于浮点数编码方法,R与优化问题定义的解每一维变量的取值范围相同。
4.交配概率Pc
决定了进化过程种群参加交配的染色体平均数目PcXN。
Pc的取值一般为0.4~0.99。
也可采用自适应的方法调整算法运行过程中的Pc值。
5.变异概率Pm
增加群体进化的多样性,决定了进化过程中群体发生变异的基因平均个数。
Pm的值不宜过大。因为变异对已找到的较优解具有一定的破坏作用,如果Pm的值太大,可能会导致算法目前所处的较好的搜索状态倒退回原来较差的情况。
Pm的取值一般为0.001~0.1。
也可采用自适应的方法调整算法运行过程中的Pm值。
6.适应值评价
影响算法对种群的选择,恰当的评估函数应该能够对染色体的优劣做出合适的区分,保证选择机制的有效性,从而提高群体的进化能力。
评估函数的设置同优化问题的求解目标有关。
评估函数应满足较优染色体的适应值较大的规定。
为了更好地提高选择的效能,可以对评估函数做出一定的修正。
目前主要的评估函数修正方法有:线性变换、乘幂变换、指数变换等
7.终止条件
决定算法何时停止运行,输出找到的最优解。
采用何种终止条件,跟具体问题的应用有关。
可以便算法在达到最大进化代数时停止,最大进化代数一殷可设置为100~1000,根据具体问题可对该建议值作相应的修改。
也可以通过考察找到的当前最优解的情况来控制算法的停止,例如,当目前进化过程算法找到的最优解达到一定的误差要求,则算法可以停止。误差范围的设置同样跟具体的优化问题相关。或者是算法在持续很长的一段时间内所找到的最优解没有得到改善时,算法可以停止。
四、GA函数的实现
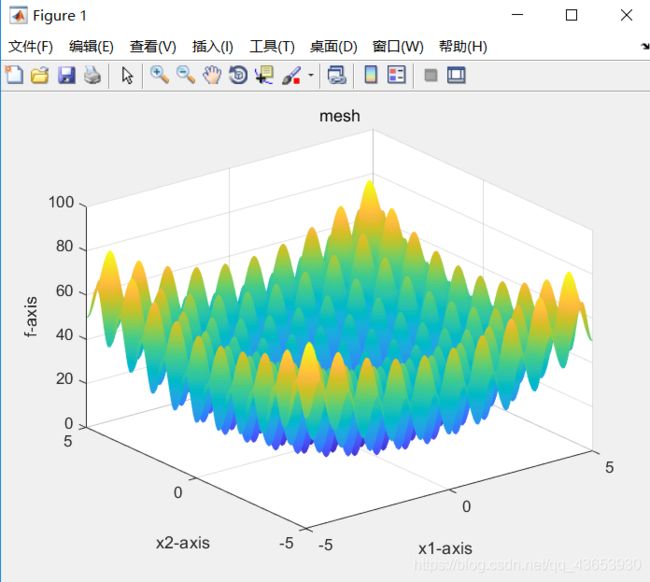
1.目标函数Griewank
function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人:
%编制日期:
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;
运行结果:
2.目标函数Rastrigin
function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
% 编制人:
% 编制日期:
[row,col] = size(x);
if row > 1
error( ' 输入的参数错误 ' );
end
y =sum(x.^2-10*cos(2*pi*x)+10);
%y =-y;运行结果:
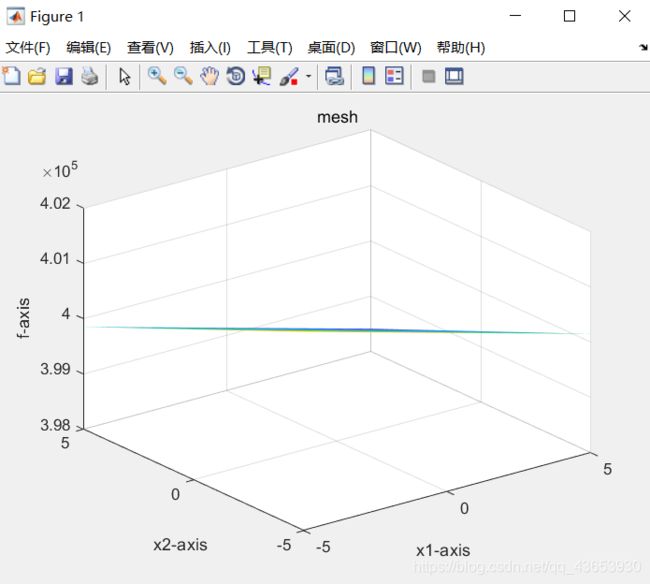
3.目标函数myfit(简单求解)
function y = myfit( x )
y = (339-0.01*x(1)-0.003*x(2))*x(1)...
+ (399-0.004*x(1)-0.01*x(2))*x(2)...
- (400000+195*x(1)+225*x(2));
y = -y; %因为GA是寻找最小值,所以为了求这个函数的最大值,取f的相反数
end
运行结果:
4.总结
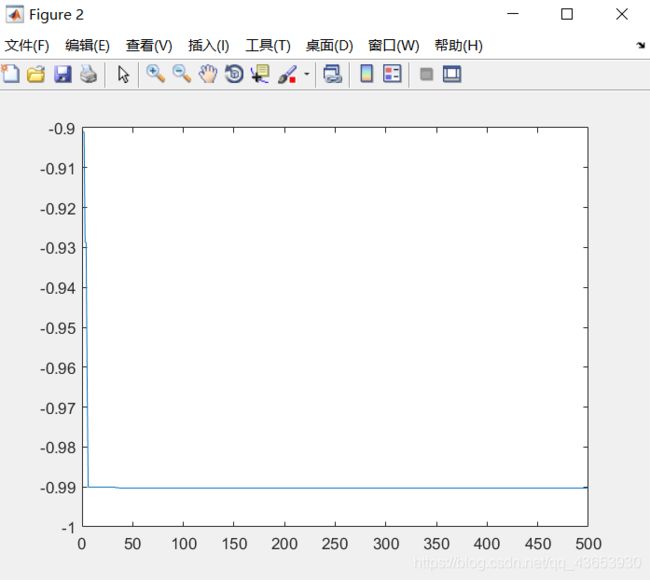
三个不同的目标函数,在种群规模、交叉变异律等其他参数设置都一样的情况下得到的最优化函数的图和表,只画二维情况作为可视化输出。第三个目标函数因为是简单的求解函数,得到的可视化二维图像不够明显,前面的两张图可以明显的观察到图形的立体形状。对比分析可以看出后面两个算法收敛的比较快,而第一个算法的起伏较大。
五、GA的优缺点
1.优点:
(1)能够求出优化问题的全局最优解。
(2)优化结果与初始条件无关。
(3)适合于求解复杂的优化问题。
2.缺点:
(1)收敛速度慢。
(2)局部搜索能力差。
(3)无确定的终止准则。
代码附录:
GA.m
% Optimizing a function using Simple Genetic Algorithm with elitist preserved
%Max f(x1,x2)=100*(x1*x1-x2).^2+(1-x1).^2; -2.0480<=x1,x2<=2.0480
%下面为代码。函数最大值为3904.9262,此时两个参数均为-2.0480,有时会出现局部极值,此时一个参数为-2.0480,一个为2.0480。变
%异概率pm=0.05,交叉概率pc=0.8。
clc;clear all;
format long;%设定数据显示格式
%初始化参数
T=500;%仿真代数
N=80;% 群体规模
pm=0.05;pc=0.8;%交叉变异概率
umax=30;umin=-30;%参数取值范围
L=10;%单个参数字串长度,总编码长度Dim*L
Dim=5;%Dim维空间搜索
bval=round(rand(N,Dim*L));%初始种群,round函数为四舍五入
bestv=-inf;%最优适应度初值
funlabel=4; %选择待优化的函数,1为Rastrigin,2为Schaffer,3为Griewank
Drawfunc(funlabel);%画出待优化的函数,只画出二维情况作为可视化输出
%迭代开始
for ii=1:T
%解码,计算适应度
for i=1:N %对每一代的第i个粒子
for k=1:Dim
y(k)=0;
for j=1:1:L %从1到L,每次加以1
y(k)=y(k)+bval(i,k*L-j+1)*2^(j-1);%把第i个粒子转化为十进制的值,例如y1是第一维
end
x(k)=(umax-umin)*y(k)/(2^L-1)+umin;%转化为实际的x1
end
% obj(i)=100*(x1*x1-x2).^2+(1-x1).^2; %目标函数
obj(i)=fun(x,funlabel);
xx(i,:)=x;
end
func=obj;%目标函数转换为适应度函数
p=func./sum(func);
q=cumsum(p);%累加
[fmax,indmax]=max(func);%求当代最佳个体
if fmax>=bestv
bestv=fmax;%到目前为止最优适应度值
bvalxx=bval(indmax,:);%到目前为止最佳位串
optxx=xx(indmax,:);%到目前为止最优参数
end
Bfit1(ii)=bestv; % 存储每代的最优适应度
%%%%遗传操作开始
%轮盘赌选择
for i=1:(N-1)
r=rand;
tmp=find(r<=q);
newbval(i,:)=bval(tmp(1),:);
end
newbval(N,:)=bvalxx;%最优保留
bval=newbval;
%单点交叉
for i=1:2:(N-1)
cc=rand;
if cc