数值计算-一维搜索收敛速度比较-matlab
为 西电数模《数值计算方法》作业
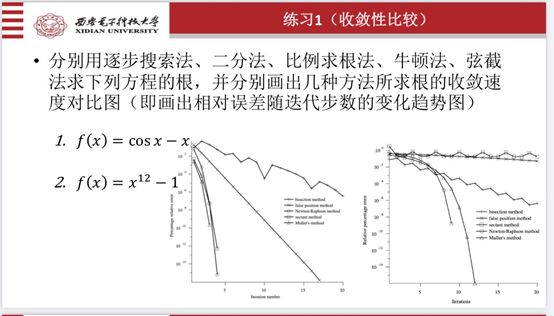
1、几种方法求根的收敛速度
逐步搜索法:
代码如下:
clear;clf
% %逐步搜索法
x0=0%任意初始点
h=1%搜索步长
eps=1e-4%精度
%比较10次
i=1
while(abs(funct(x0))>=eps)
x1=x0+h
y1(i)=abs(x1-0.7391)/0.7391
i=i+1
if(i==11)
break
end
if(abs(funct(x1))=eps)
x=(a+b)/2
y2(i)=abs(x-0.7391)/0.7391
i=i+1
if(i==11)
break;
end
if(funct(x)>=0)
a=x
else
b=x
end
end
plot(y2)
% %比例求根法
x0=0
q=0.618
a=0;b=2%初始区间
c = a - funct(a)/(funct(a)-funct(b))*(a-b)
i=1
while(abs(funct(c))>=eps)
c = a - funct(a)/(funct(a)-funct(b))*(a-b)
y3(i)=abs(c-0.7391)/0.7391
i=i+1
if(i==11)
break;
end
if(funct(c)*funct(a)>=0)
a=c
else
b=c
end
end
plot(y3)
%
%牛顿法
x0=0
syms z
f(z)=cos(z)-z
dx=diff(f(z),1)
%subs(dx,'z',1)
dxx=diff(dx,1)
f=matlabFunction(f(z))
fdx=matlabFunction(dx)
fdxx=matlabFunction(dxx)
x=x0-fdx(x0)/fdxx(x0)
i=1
while(abs(fdx(x))>=eps)
y4(i)=abs(x-0.7391)/0.7391
i=i+1
if(i==11)
break;
end
x=x0-f(x0)/fdx(x0)
x0=x
end
plot(y4)
%弦截法
a=0;b=2
i=1
x=(a*funct(b)-b*funct(a))/(funct(b)-funct(a))
while(funct(x)>=eps)
y5(i)=abs(x-0.7391)/0.7391
i=i+1
if(i==11)
break;
end
x=(a*funct(b)-b*funct(a))/(funct(b)-funct(a))
if(funct(x)*funct(a)<0)
b=x
else
a=x
end
end
plot(y5)
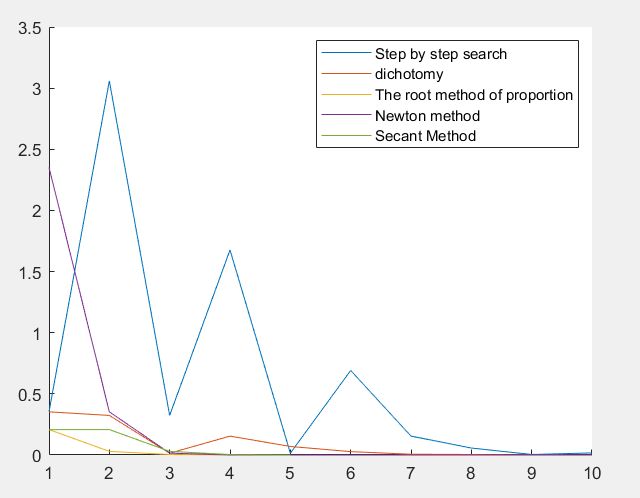
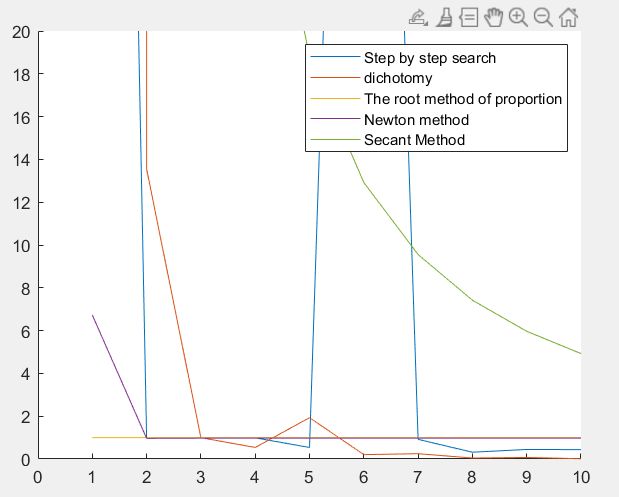
legend('Step by step search','dichotomy','The root method of proportion','Newton method','Secant Method')
对于函数 f ( x ) = c o x ( x ) − x f(x)=cox(x)-x f(x)=cox(x)−x
对于函数 f ( x ) = x 12 − 1 f(x)=x^{12}-1 f(x)=x12−1
注:初值和初始区间的选取有变
2、根的迭代
要求左下角的根,不妨设初值 x 0 = − 2 a n d y 0 = − 1 x_{0}=-2 and y_{0}=-1 x0=−2andy0=−1
f ( x 0 , y 0 ) = 1 , g ( x 0 , y 0 ) = − 1.3679 f(x_{0},y_{0})=1,g(x_{0},y_{0})=-1.3679 f(x0,y0)=1,g(x0,y0)=−1.3679
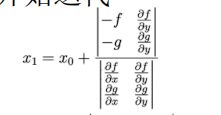
迭代公式:
因此, x 1 = − 2.7348 , y 1 = − 0.7652 x_{1}= -2.7348,y_{1}=-0.7652 x1=−2.7348,y1=−0.7652
x 2 = − 2.5128 , y 2 = − 0.9495 x_{2}= -2.5128,y_{2}= -0.9495 x2=−2.5128,y2=−0.9495
x 3 = − 2.5125 , y 3 = − 0.9190 x_{3}= -2.5125,y_{3}= -0.9190 x3=−2.5125,y3=−0.9190
而精确计算可得,左下角的根为: x = − 2.5122110252087035675465931953423 , y = − 0.9189 x= -2.5122110252087035675465931953423,y=-0.9189 x=−2.5122110252087035675465931953423,y=−0.9189
代码如下:
clear;clf
x0= -2;y0= -1
x=-2.5122110252087035675465931953423;y= -0.9189
i=1
while(i<=4)%迭代四次
m=f1([x0,y0])
n=g1([x0,y0])
a=[-m,4*y0;-n,1]
b=[2*x0,4*y0;exp(x0),1]
x1=x0+det(a)/det(b)
c=[2*x0,-m;exp(x0),-n]
d=[2*x0,4*y0;exp(x0),1]
y1=y0+det(c)/det(d)
x0=x1;y0=y1
i=i+1
end
n=g1([x0,y0])
a=[-m,4y0;-n,1]
b=[2x0,4y0;exp(x0),1]
x1=x0+det(a)/det(b)
c=[2x0,-m;exp(x0),-n]
d=[2x0,4y0;exp(x0),1]
y1=y0+det©/det(d)
x0=x1;y0=y1
i=i+1
end
注:选取的初值必须非常靠近精确解,若取(-1,-2)则不收敛