CenterNet论文学习解读

资源

论文题目： Objects as Points

论文地址：https://arxiv.org/pdf/1904.07850.pdf

发布时间：2019.4.16

机构：UT Austin，UC Berkeley

代码：https://github.com/xingyizhou/CenterNet

相关解读：(本文是基于这两篇文章的学习整理)

https://blog.csdn.net/c20081052/article/details/89358658

https://zhuanlan.zhihu.com/p/66048276

原理

简介

此检测器采用关键点估计来找到中心点，并回归到其他目标属性，例如尺寸，3D位置，方向，甚至姿态。

• 对于2D BBox检测， 先生成热力图找到关键点，再回归关键点在特征图和原图间的偏移，再回归宽高

• 对于3D BBox检测，我们直接回归得到目标的深度信息，3D框的尺寸，目标朝向

• 对于人姿态估计，我们将关节点（2D joint）位置作为中心点的偏移量，直接在中心点位置回归出这些偏移量的值

相关研究

使用anchor的目标检测

• fast-rcnn

一组候选框中枚举出目标框,再对每个对象进行卷积分类

---

• faster-rcnn

卷积网络中生成候选区域区域， IOU > 0.7作为前景，否则为背景，再进行分类

---

优势

1. 仅在目标位置设置关键点，没有了全图枚举或区域提案RPN生成检测框，不用设置阈值做前后框分类
2. 不需要NMS后处理来去除重复检测框。
3. 使用更大的分辨率（缩放4倍），传统目标检测缩放16倍

总体来说，CenterNet结构优雅简单，直接检测目标的中心点和大小，是真anchor-free。比其他方法更简单，更快。

使用关键点的目标检测

• ExtremeNet

检测所有目标的 最上，最下，最左，最右，中心点

---

• CornerNet

将bbox的两个角作为关键点

---

优势

它们都需要经过一个关键点grouping阶段(对关键点以人为单位分组，具体没去看)，这会降低算法整体速度，centernet仅仅提取每个目标的中心点，无需对关键点进行grouping 或者是后处理

---

单目3D目标检测

• Deep3Dbox

使用一个 slow-RCNN 风格的框，该网络先检测2D目标，然后将目标送到3D 估计网络

---

• 3D RCNN

在Faster-RCNN上添加了额外的head来做3D projection

---

• Deep Manta

使用一个 coarse-to-fine的Faster-RCNN ，在多任务中训练

---

优势

同one-stage版本的Deep3Dbox 或3D RCNN相似，同样，CenterNet比它们都更简洁，更快。

---

网络结构

预备知识

令 $I\in R^{W\times H\times 3}$为输出图像,其宽W，高H。

• 关键点热力图定义, R 是输出stride（即尺寸缩放比例）,默认为4， C是关键点类型数（即输出特征图通道数）,C=80,则为COCO目标类别，C=17，则为COCO姿态点.

$$\hat{Y}\in [0,1{]}^{\frac{W}{R}\times \frac{H}{R}\times C}$$

• ${\hat{Y}}_{x,y,c}=1$ 表示检测到的关键点

• ${\hat{Y}}_{x,y,c}=0$ 表示背景

• 将真实关键点分布到特征图上， 真实关键点$p\in R^2$ 对于下采样后的坐标，我们设为$\tilde{p}=|\frac{p}{R}|$，通过高斯核分散到热力图$\hat{Y}$上，如果对于同个类 c （同个关键点或是目标类别）有两个高斯函数发生重叠，我们选择元素级最大的。

$$Y_{xyc}=exp(-\frac{(x-{\tilde{p}}_x{)}^2+(y-{\tilde{p}}_y{)}^2}{2{\sigma }_p^2})$$

高斯生成的中心点

损失函数

• 中心点损失函数，像素级逻辑回归的focal loss

$$L_k=\frac{-1}{N}\sum \{\begin{array}{l}(1-{\hat{Y}}_{xyc}{)}^{\alpha }log({\hat{Y}}_{xyc}),if{Y}_{xyc}=1\\ \\ (1-Y_{xyc}{)}^{\beta }({\hat{Y}}_{xyc}{)}^{\alpha }log(1-{\hat{Y}}_{xyc}),otherwise\end{array}$$
其中 $\alpha$ 和$\beta$是focal loss的超参数，实验中两个数分别设置为2和4， N是图像 I 中的关键点个数，除以N主要为了将所有focal loss归一化。

解读：

如果预测的中心点真值为1，那该点为易学目标，更加减小预测正确的损失值，增大错误的损失值。

如果预测的中心点真值不为1，真值中心点很少，正负样本不均衡，通过$(1-Y_{xyc}{)}^{\beta }$加大远离真值为1的中心点损失值，减小靠近真值1的中心点损失值。靠近真实点的地方为易学点通过$({\hat{Y}}_{xyc}{)}^{\alpha }$增大靠近真实点预测错误的损失值，$(1-Y_{xyc}{)}^{\beta }$和$({\hat{Y}}_{xyc}{)}^{\alpha }$在靠近真实点处相互牵制

• 目标中心的偏置损失,下采样4倍的真实关键点可能为小数，而预测点为整数，映射到原始图像，会有精度误差，这个偏置值用L1 loss来训练

$$L_{off}=\frac{1}{N}\sum _p|{\hat{O}}_{\tilde{p}}-(\frac{P}{R}-\tilde{p})|$$
${\hat{O}}_{\tilde{p}}$ 是我们预测出来的偏置，$(\frac{P}{R}-\tilde{p})$则是在训练过程中提前计算出来的实际误差

• 目标大小的损失，对每个目标的size进行回归，最终回归到 $s_k=(x_2^{(2)}-x_1^{(2)},y_2^{(2)}-y_1^{(2)})$，使用L1 loss来训练

$$L_{size}=\frac{1}{N}\sum _{k=1}^N|{\hat{S}}_{p_k}-s_k|$$

• 整体的损失函数为物体损失、大小损失与偏置损失的和，每个损失都有相应的权重

$$L_{det}=L_k+{\lambda }_{size}{L}_{size}+{\lambda }_{off}{L}_{off}$$

---

推理

2D检测

找到关键点：
在推理的时候，我们分别提取热力图上每个类别的峰值点。如何得到这些峰值点呢？做法是将热力图上的所有响应点与其连接的8个临近点进行比较，如果该点响应值大于或等于其八个临近点值则保留，最后我们保留所有满足之前要求的前100个峰值点

产生bbox：$(\delta {\hat{x}}_i,\delta {\hat{y}}_i)$为偏移预测结果，$({\hat{w}}_i,{\hat{h}}_i)$为宽高预测结果
$$\begin{gathered} ({\hat{x}}_i+\delta {\hat{x}}_i-{\hat{w}}_i/2,{\hat{y}}_i+\delta {\hat{y}}_i-{\hat{h}}_i/2, \\ {\hat{x}}_i+\delta {\hat{x}}_i+{\hat{w}}_i/2,{\hat{y}}_i+\delta {\hat{y}}_i+{\hat{h}}_i/2) \end{gathered}$$

---

3D检测：

每个中心点需要3个附加信息:depth, 3D dimension， orientation。我们为每个信息分别添加head.

depth:对于每个中心点，深度值depth是一个维度的, 然后depth很难直接回归, 在特征点估计网络上添加了一个深度计算通道$\hat{D}\in [0,1{]}^{\frac{W}{R}\times \frac{H}{R}}$， 该通道使用了两个卷积层，然后做ReLU 。输出为$d=1/\sigma (\hat{d})-1$,$ \sigma$为sigmoid函数，我们用L1 loss来训练深度估计器。

3D维度:目标的3D维度是三个标量值。我们直接回归出它们（长宽高）的绝对值，单位为米，用的是一个独立的head,和L1 loss

方向：方向默认是单标量的值，然而其也很难回归。用两个bins来呈现方向，且i做n-bin回归。特别地，方向用8个标量值来编码的形式，每个bin有4个值。对于一个bin,两个值用作softmax分类，其余两个值回归到在每个bin中的角度。

人体姿态估计

设人体关键点为$k$

1. 通过中心点，回归出$k$个关节点的偏移$\hat{J}\in R^{\frac{W}{R}\times \frac{H}{R}\times k\times 2}$,得到关节点$l_j=(\hat{x},\hat{y})+{\hat{J}}_{\hat{x}\hat{y}j}forj\in 1...k$用到了L1 loss,我们通过给loss添加mask方式来无视那些不可见的关键点（关节点）。此处参照了slow-RCNN。
2. 估计$k$个人体关节点热力图,检测出所有人体关键点(热力图上值小于0.1的直接略去)。使用focal loss和像素偏移量。
3. 分配关节点到人，将第一步的中心偏移$\hat{J}$ 作为一个grouping的线索，来为每个关键点（关节点）分配其最近的人,回归得到的位置$l_j$与最近的检测关节点进行分配$arg{\min }_{l\in L_j}(l-l_j{)}^2$ ,只对检测到的目标框中的关节点进行关联。

backbone

我们实验了4个结构：ResNet-18, ResNet-101, DLA-34， Hourglass-104. 我们用deformable卷积层来更改ResNets和DLA-34，按照原样使用Hourglass 网络

---

• Resnet-18 with up-convolutional layers : 28.1% coco and 142 FPS

Xiao et al. [55]等人对标准的ResNet做了3个up-convolutional网络来得到更高的分辨率输出（最终stride为4）。为了节省计算量，我们改变这3个up-convolutional的输出通道数分别为256,128,64。up-convolutional核初始为双线性插值。

---

• DLA-34 : 37.4% COCOAP and 52 FPS

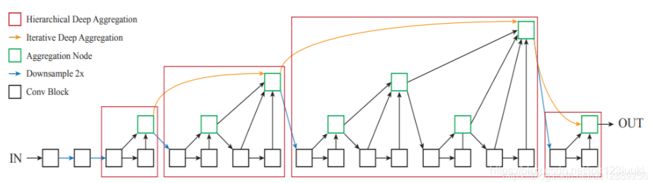
即Deep Layer Aggregation (DLA)，是带多级跳跃连接的图像分类网络，我们采用全卷积上采样版的DLA，用deformable卷积来跳跃连接低层和输出层；将原来上采样层的卷积都替换成3x3的deformable卷积。在每个输出head前加了一个3x3x256的卷积，然后做1x1卷积得到期望输出。

---

• Hourglass-104 : 45.1% COCOAP and 1.4 FPS

堆叠的Hourglass网络，通过两个连续的hourglass 模块对输入进行了4倍的下采样，每个hourglass 模块是个对称的5层 下和上卷积网络，且带有skip连接。该网络较大，但通常会生成最好的关键点估计。

---

(a):Hourglass

(b):使用反卷积的ResNet

(c ):DLA-34

(d):DLA-34，底层添加了更多的跳转连接，并对每个卷积层替换为可变形卷积层的上采样阶段

代码解读

创建模型

 model = get_model(num_layers=num_layers, heads=heads, head_conv=head_conv)

• num_layers 为选择num_layers层的resnet网络

• heads 为需要输出的特征有哪些，比如coco目标检测模型，输出80类热力图，宽高，偏移

 if opt.task == 'exdet':
      # assert opt.dataset in ['coco']
      num_hm = 1 if opt.agnostic_ex else opt.num_classes
      opt.heads = {'hm_t': num_hm, 'hm_l': num_hm, 
                   'hm_b': num_hm, 'hm_r': num_hm,
                   'hm_c': opt.num_classes}
      if opt.reg_offset:
        opt.heads.update({'reg_t': 2, 'reg_l': 2, 'reg_b': 2, 'reg_r': 2})
    elif opt.task == 'ddd':
      # assert opt.dataset in ['gta', 'kitti', 'viper']
      opt.heads = {'hm': opt.num_classes, 'dep': 1, 'rot': 8, 'dim': 3}
      if opt.reg_bbox:
        opt.heads.update(
          {'wh': 2})
      if opt.reg_offset:
        opt.heads.update({'reg': 2})
    elif opt.task == 'ctdet':
      # assert opt.dataset in ['pascal', 'coco']
      opt.heads = {'hm': opt.num_classes,
                   'wh': 2 if not opt.cat_spec_wh else 2 * opt.num_classes}
      if opt.reg_offset:
        opt.heads.update({'reg': 2})
    elif opt.task == 'multi_pose':
      # assert opt.dataset in ['coco_hp']
      # opt.flip_idx = dataset.flip_idx
      opt.flip_idx = False
      opt.heads = {'hm': opt.num_classes, 'wh': 2, 'hps': 34}
      if opt.reg_offset:
        opt.heads.update({'reg': 2})
      if opt.hm_hp:
        opt.heads.update({'hm_hp': 17})
      if opt.reg_hp_offset:
        opt.heads.update({'hp_offset': 2})

• head_conv 输出通道数

    if opt.head_conv == -1: # init default head_conv
      opt.head_conv = 256 if 'dla' in opt.arch else 64

resnet_dcn

• resnet是由多个block构成一个layer，再有多个layer组成的残差网络，残差结构是下图的dawnsample

• resnet18的block结构

block

block_with_dawnsample

x_1

conv1_b

bn1_b

relu1_b

conv2_b

bn2_b

relu2_b

x

conv1_bd

bn1_bd

relu_bd

conv2_bd

bn2_bd

conv_ds

bn_ds

relu2_bd

• BasicBlock前向传播

def forward(self, x):
    residual = x

    out = self.conv1(x)
    out = self.bn1(out)
    out = self.relu(out)

    out = self.conv2(out)
    out = self.bn2(out)

    if self.downsample is not None:
        residual = self.downsample(x)

    out += residual
    out = self.relu(out)

    return out

• layper网络定义

def _make_layer(self, block, planes, blocks, stride=1):
    downsample = None
    if stride != 1 or self.inplanes != planes * block.expansion:
        downsample = nn.Sequential(
            nn.Conv2d(self.inplanes, planes * block.expansion,
                      kernel_size=1, stride=stride, bias=False),
            nn.BatchNorm2d(planes * block.expansion, momentum=BN_MOMENTUM),
        )

    layers = []
    layers.append(block(self.inplanes, planes, stride, downsample))
    self.inplanes = planes * block.expansion
    for i in range(1, blocks):
        layers.append(block(self.inplanes, planes))

    return nn.Sequential(*layers)

• deconv_layers x 3

deconv_layers

DCN

bn1

relu1

ConvTranspose2d

relu2

DCN部分是cuda代码，我看不懂，之后会专门开一篇文章将DCN

• 可变形卷积+反卷积网络定义

def _make_deconv_layer(self, num_layers, num_filters, num_kernels):
    assert num_layers == len(num_filters), \
        'ERROR: num_deconv_layers is different len(num_deconv_filters)'
    assert num_layers == len(num_kernels), \
        'ERROR: num_deconv_layers is different len(num_deconv_filters)'

    layers = []
    for i in range(num_layers):
        kernel, padding, output_padding = \
            self._get_deconv_cfg(num_kernels[i], i)

        planes = num_filters[i]
        fc = DCN(self.inplanes, planes, 
                kernel_size=(3,3), stride=1,
                padding=1, dilation=1, deformable_groups=1)
        # fc = nn.Conv2d(self.inplanes, planes,
        #         kernel_size=3, stride=1, 
        #         padding=1, dilation=1, bias=False)
        # fill_fc_weights(fc)
        up = nn.ConvTranspose2d(
                in_channels=planes,
                out_channels=planes,
                kernel_size=kernel,
                stride=2,
                padding=padding,
                output_padding=output_padding,
                bias=self.deconv_with_bias)
        fill_up_weights(up)

        layers.append(fc)
        layers.append(nn.BatchNorm2d(planes, momentum=BN_MOMENTUM))
        layers.append(nn.ReLU(inplace=True))
        layers.append(up)
        layers.append(nn.BatchNorm2d(planes, momentum=BN_MOMENTUM))
        layers.append(nn.ReLU(inplace=True))
        self.inplanes = planes

    return nn.Sequential(*layers)

• resnet18_dcn

layer5

layer4

layer3

layer2

layer1

conv1

block8

deconv_layers

block6

block7

block4

block5

block2

block3

maxpool

block1

conv1

bn1

relu

hm_head

wh_head

reg_head

• resnet18_dcn前向传播

def forward(self, x):
    x = self.conv1(x)
    x = self.bn1(x)
    x = self.relu(x)
    x = self.maxpool(x)

    x = self.layer1(x)
    x = self.layer2(x)
    x = self.layer3(x)
    x = self.layer4(x)

    x = self.deconv_layers(x)
    ret = {}
    for head in self.heads:
        ret[head] = self.__getattr__(head)(x)
    return [ret]

• 输出head网络定义

for head in self.heads:
    classes = self.heads[head]
    if head_conv > 0:
        fc = nn.Sequential(
          nn.Conv2d(64, head_conv,
            kernel_size=3, padding=1, bias=True),
          nn.ReLU(inplace=True),
          nn.Conv2d(head_conv, classes, 
            kernel_size=1, stride=1, 
            padding=0, bias=True))
        if 'hm' in head:
            fc[-1].bias.data.fill_(-2.19)
        else:
            fill_fc_weights(fc)
    else:
        fc = nn.Conv2d(64, classes, 
          kernel_size=1, stride=1, 
          padding=0, bias=True)
        if 'hm' in head:
            fc.bias.data.fill_(-2.19)
        else:
            fill_fc_weights(fc)
    self.__setattr__(head, fc)

dla34_dcn

• dla34_dcn包含dla34以及dlaup解码(上采样)两部分

• dla34_dcn

dla34_dcn

ida_up最后一层

ida_up最后一层

ida_up最后一层

x

dla_base

dla_up

ida_up

hm_head

wh_head

reg_head

• dla34_dcn前向传播

def forward(self, x):
    x = self.base(x)
    x = self.dla_up(x)

    y = []
    for i in range(self.last_level - self.first_level):
        y.append(x[i].clone())
    self.ida_up(y, 0, len(y))

    z = {}
    for head in self.heads:
        z[head] = self.__getattr__(head)(y[-1])
    return [z]

• dla34 网络结构

level5

tree

level4

tree

tree

level3

tree

tree

level2

tree

level1

level0

base_layer

downsample

project

downsample

project

downsample

project

downsample

project

downsample

project

downsample

project

root4_2

bottom5_1

block5_1

block5_2

root5

root4_1

block4_3

bottom4_2

block4_4

root3_2

bottom4_1

block4_1

block4_2

root3_1

block3_3

bottom3_2

block3_4

root

bottom3_1

block3_1

block3_2

relu1

bottom2_1

block_1

block_2

Conv1

bn1

Conv0

bn0

relu0

Conv_b

bn_b

relu_b

x

• dla34前向传播

def forward(self, x):
    y = []
    x = self.base_layer(x)
    for i in range(6):
        x = getattr(self, 'level{}'.format(i))(x)
        y.append(x)
    return y

• dla34网络定义

def __init__(self, levels, channels, num_classes=1000,
             block=BasicBlock, residual_root=False, linear_root=False):
    super(DLA, self).__init__()
    self.channels = channels
    self.num_classes = num_classes
    self.base_layer = nn.Sequential(
        nn.Conv2d(3, channels[0], kernel_size=7, stride=1,
                  padding=3, bias=False),
        nn.BatchNorm2d(channels[0], momentum=BN_MOMENTUM),
        nn.ReLU(inplace=True))
    self.level0 = self._make_conv_level(
        channels[0], channels[0], levels[0])
    self.level1 = self._make_conv_level(
        channels[0], channels[1], levels[1], stride=2)
    self.level2 = Tree(levels[2], block, channels[1], channels[2], 2,
                       level_root=False,
                       root_residual=residual_root)
    self.level3 = Tree(levels[3], block, channels[2], channels[3], 2,
                       level_root=True, root_residual=residual_root)
    self.level4 = Tree(levels[4], block, channels[3], channels[4], 2,
                       level_root=True, root_residual=residual_root)
    self.level5 = Tree(levels[5], block, channels[4], channels[5], 2,
                       level_root=True, root_residual=residual_root)

• tree前向传播

def forward(self, x, residual=None, children=None):
    children = [] if children is None else children
    bottom = self.downsample(x) if self.downsample else x
    residual = self.project(bottom) if self.project else bottom
    if self.level_root:
        children.append(bottom)
    x1 = self.tree1(x, residual)
    if self.levels == 1:
        x2 = self.tree2(x1)
        x = self.root(x2, x1, *children)
    else:
        children.append(x1)
        x = self.tree2(x1, children=children)
    return x

• tree网络定义

def __init__(self, levels, block, in_channels, out_channels, stride=1,
             level_root=False, root_dim=0, root_kernel_size=1,
             dilation=1, root_residual=False):
    super(Tree, self).__init__()
    if root_dim == 0:
        root_dim = 2 * out_channels
    if level_root:
        root_dim += in_channels
    if levels == 1:
        self.tree1 = block(in_channels, out_channels, stride,
                           dilation=dilation)
        self.tree2 = block(out_channels, out_channels, 1,
                           dilation=dilation)
    else:
        self.tree1 = Tree(levels - 1, block, in_channels, out_channels,
                          stride, root_dim=0,
                          root_kernel_size=root_kernel_size,
                          dilation=dilation, root_residual=root_residual)
        self.tree2 = Tree(levels - 1, block, out_channels, out_channels,
                          root_dim=root_dim + out_channels,
                          root_kernel_size=root_kernel_size,
                          dilation=dilation, root_residual=root_residual)
    if levels == 1:
        self.root = Root(root_dim, out_channels, root_kernel_size,
                         root_residual)
    self.level_root = level_root
    self.root_dim = root_dim
    self.downsample = None
    self.project = None
    self.levels = levels
    if stride > 1:
        self.downsample = nn.MaxPool2d(stride, stride=stride)
    if in_channels != out_channels:
        self.project = nn.Sequential(
            nn.Conv2d(in_channels, out_channels,
                      kernel_size=1, stride=1, bias=False),
            nn.BatchNorm2d(out_channels, momentum=BN_MOMENTUM)
        )

• 解释

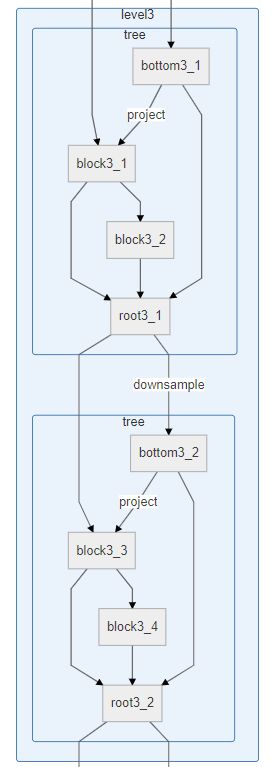
右图为layer3的结构，红圈内为一个tree，黑框为block，绿框为root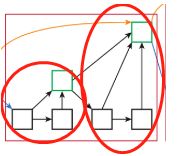

与下图的两个tree相对应，

• block

#残差结构

block

x

conv1

bn1

relu1

conv2

bn2

relu2

conv3

bn3

relu3

• block前向传播

    def forward(self, x, residual=None):
        if residual is None:
            residual = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)
        out = self.relu(out)

        out = self.conv3(out)
        out = self.bn3(out)

        out += residual
        out = self.relu(out)

        return out

• DLAUp

使用多个ida将各layer的结果链接起来,如下图橙色部分, 红框为layer2~5

• DLAUp前向传播

#执行多个ida
def forward(self, layers):
    out = [layers[-1]] # start with 32
    for i in range(len(layers) - self.startp - 1):
        ida = getattr(self, 'ida_{}'.format(i))
        ida(layers, len(layers) -i - 2, len(layers))
        out.insert(0, layers[-1])
    return out

• ida前向传播

def forward(self, layers, startp, endp):
    for i in range(startp + 1, endp):
        upsample = getattr(self, 'up_' + str(i - startp))
        project = getattr(self, 'proj_' + str(i - startp))
        layers[i] = upsample(project(layers[i]))
        node = getattr(self, 'node_' + str(i - startp))
        layers[i] = node(layers[i] + layers[i - 1])

关键代码 :layers[i] = node(layers[i] + layers[i - 1])

将两个layer的结果相加，对应上图橙色箭头

• ida网络定义

    def __init__(self, o, channels, up_f):
        super(IDAUp, self).__init__()
        for i in range(1, len(channels)):
            c = channels[i]
            f = int(up_f[i])  
            proj = DeformConv(c, o)
            node = DeformConv(o, o)
     
            up = nn.ConvTranspose2d(o, o, f * 2, stride=f, 
                                    padding=f // 2, output_padding=0,
                                    groups=o, bias=False)
            fill_up_weights(up)

            setattr(self, 'proj_' + str(i), proj)
            setattr(self, 'up_' + str(i), up)
            setattr(self, 'node_' + str(i), node)