目标检测学习笔记——map概念、IoU汇总Iou、Giou、Ciou、Diou

目标检测学习笔记——map概念、IoU汇总Iou、Giou、Ciou、Diou

---

---

前言

---

一、什么是map值？

map是Mean Average Precision 的缩写（均值平均精度）
介绍map之前，先了解以下概念
TP：True Positive，分类器预测结果为正样本，实际也为正样本，即正样本被正确识别的数量。
FP：False Positive，分类器预测结果为正样本，实际为负样本，即误报的负样本数量。
TN：True Negative，分类器预测结果为负样本，实际为负样本，即负样本被正确识别的数量。
FN：False Negative，分类器预测结果为负样本，实际为正样本，即漏报的正样本数量。
TP+FN：真实正样本的总和，正确分类的正样本数量+漏报的正样本数量。
FP+TN：真实负样本的总和，负样本被误识别为正样本数量+正确分类的负样本数量。
TP+TN：正确分类的样本总和，正确分类的正样本数量+正确分类的负样本数量。

Precision：查准率、精度

Precision表征的是预测正确的正样本的准确度，查准率等于预测正确的正样本数量/所有预测为正样本数量。Precision越大说明误检的越少，Precision越小说明误检的越多。
Precision=TP/(TP+FP)

Recall：查全率、召回率

Recall表征的是预测正确的正样本的覆盖率，查全率等于预测正确的正样本数量/所有正样本的总和，TP+FN实际就是Ground Truth的数量。Recall越大说明漏检的越少，Recall越小说明漏检的越多。
Recall=TP/(TP+FN)

对于目标检测来说，每一个类都可以计算出Precision和Recall，每个类都可以得到一条P-R曲线（P-R曲线，顾名思义，就是P-R的关系曲线图，表示了召回率和准确率之间的关系），曲线下的面积就是AP（平均精确度）的值。对所有AP的值求平均就是map。

二、IoU汇总Iou、Giou、Ciou、Diou

2.1 Iou

Iou通俗来说也就是交并比，计算不同图像相互重叠比例。
$$IoU=\frac{A\cap B}{A\cup B}$$

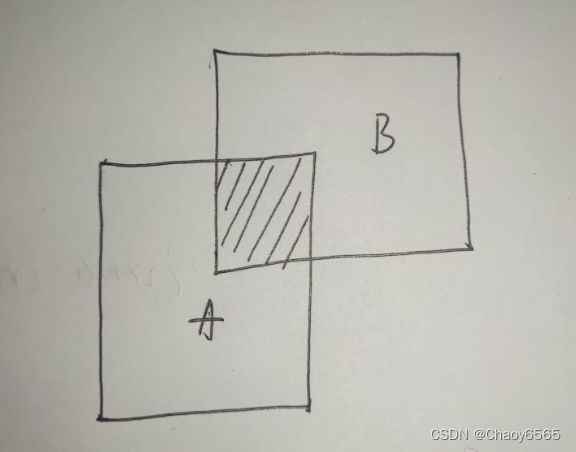
IoU Loss具有非负性、尺度不变性、同一性、对称性、三角不等性等特点,但是如果|A∩B|=0,也就是两个图像没有相交时，无法比较两个图像的距离远近，无法体现两个图像到底是如何相交的。

2.2 Giou

GIoU比IoU多了一个‘Generalized’，能在更广义的层面上计算IoU，解决了两个图像没有相交时，无法比较两个图像的距离远近的问题。
$$GIOU=IoU-\frac{\left|C-A\cup B\right|}{C}$$
其中C代表两个图像的最小包庇面积，也可以理解为这两个图像的最小外接矩形的面积。GIoU不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度。GIoU完善了图像重叠度的计算功能，但仍无法对图形距离以及长宽比的相似性进行很好的表示。

2.3Diou

DIoU（Distance-IoU)将两个框之间的重叠度、距离、尺度都考虑了进来。
$$Diou=Iou-\frac{{\rho }^2(b,b^{gt})}{c^2}$$
其中b，bgt分别代表两个框的中心点，ρ代表两个中心点之间的欧氏距离，C代表最小包庇矩形的对角线。
预测框和真实框的重叠程度。并且考虑到预测框长和宽的比值问题并以此添加惩罚项，从而使预测框的效果更加稳定
DIoU在完善图像重叠度的计算功能的基础上，实现了对图形距离的考量，但仍无法对图形长宽比的相似性进行很好的表示。

2.4 Ciou

可以看出，CIoU就是在DIoU的基础上，增加了图像相似性的影响因子，因此可以更好的反映两个框之间的差异性。
我们还需要注意的一点是，在使用CIoU作为Loss的时候，v的梯度同样会参与反向传播的计算。

2.5 代码

图片以左上角为中心点

# 以左上角为中心点
# box:[上, 左, 下, 右]
import numpy as np
import math

def IoU(box1, box2):
    # 计算中间矩形的宽高
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])
    
    # 计算交集、并集面积
    inter = 0 if in_h < 0 or in_w < 0 else in_h * in_w
    union = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
            (box2[2] - box2[0]) * (box2[3] - box2[1]) - inter
    # 计算IoU
    iou = inter / union
    return iou

def GIoU(box1, box2):
    # 计算最小包庇面积
    y1,x1,y2,x2 = box1 
    y3,x3,y4,x4 = box2
    area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4)) * \
             (max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
    
    # 计算IoU
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])
    inter = 0 if in_h < 0 or in_w < 0 else in_h * in_w
    union = (box1[2] - box1[0]) * (box1[3] - box1[1]) + \
            (box2[2] - box2[0]) * (box2[3] - box2[1]) - inter
    iou = inter / union
    
    # 计算空白部分占比
    end_area = (area_C - union)/area_C
    giou = iou - end_area
    return giou

def CIoU(box1, box2):
    y1,x1,y2,x2 = box1 
    y3,x3,y4,x4 = box2
    
    iou = IoU(box1, box2)
    diou = DIoU(box1, box2)
 
    v = 4 / math.pi**2 * (math.atan((x2-x1)/(y2-y1)) - \
                          math.atan((x4-x3)/(y4-y3)))**2 + 1e-5
    alpha = v / ((1-iou) + v)
    
    ciou = diou - alpha * v
    return ciou

def DIoU(box1, box2):
    # 计算对角线长度
    y1,x1,y2,x2 = box1 
    y3,x3,y4,x4 = box2
    C = np.sqrt((max(x1,x2,x3,x4)-min(x1,x2,x3,x4))**2 + \
                (max(y1,y2,y3,y4)-min(y1,y2,y3,y4))**2)
    
    # 计算中心点间距
    point_1 = ((x2+x1)/2, (y2+y1)/2)
    point_2 = ((x4+x3)/2, (y4+y3)/2)
    D = np.sqrt((point_2[0]-point_1[0])**2 + \
                (point_2[1]-point_1[1])**2)
 
    # 计算IoU
    iou = IoU(box1, box2)
 
    # 计算空白部分占比
    lens = D**2 / C**2
    diou = iou - lens
    return diou

输出

# box:[上, 左, 下, 右]
box1 = [0,0,8,6]
box2 = [2,3,10,9]
print('Iou',IoU(box1, box2))
print('GIou',GIoU(box1, box2))
print('DIou',DIoU(box1, box2))
print('CIou',CIoU(box1, box2))

以h，w中心为中心点

import numpy as np
import torch
import math

def Iou(box1, box2, wh=False):
    if wh == False:
        xmin1, ymin1, xmax1, ymax1 = box1
        xmin2, ymin2, xmax2, ymax2 = box2
    else:
        xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)
        xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)
        xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)
        xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)
        
    # 获取矩形框交集对应的左上角和右下角的坐标（intersection）
    xx1 = np.max([xmin1, xmin2])
    yy1 = np.max([ymin1, ymin2])
    xx2 = np.min([xmax1, xmax2])
    yy2 = np.min([ymax1, ymax2])
    # 计算两个矩形框面积
    area1 = (xmax1-xmin1) * (ymax1-ymin1) 
    area2 = (xmax2-xmin2) * (ymax2-ymin2)
    inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))   # 计算交集面积
    iou = inter_area / (area1+area2-inter_area+1e-6)    # 计算交并比
    return iou

def Giou(rec1,rec2):
    #分别是第一个矩形左右上下的坐标
    x1,x2,y1,y2 = rec1 
    x3,x4,y3,y4 = rec2
    iou = Iou(rec1,rec2)
    area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))
    area_1 = (x2-x1)*(y1-y2)
    area_2 = (x4-x3)*(y3-y4)
    sum_area = area_1 + area_2

    w1 = x2 - x1   #第一个矩形的宽
    w2 = x4 - x3   #第二个矩形的宽
    h1 = y1 - y2
    h2 = y3 - y4
    W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)    #交叉部分的宽
    H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)    #交叉部分的高
    Area = W*H    #交叉的面积
    add_area = sum_area - Area    #两矩形并集的面积

    end_area = (area_C - add_area)/area_C    #闭包区域中不属于两个框的区域占闭包区域的比重
    giou = iou - end_area
    return giou

def Diou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    dious = torch.zeros((rows, cols))
    if rows * cols == 0:
        return dious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        dious = torch.zeros((cols, rows))
        exchange = True
    # #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]
    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1] 
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]
    
    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2 
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2 
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:]) 
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2]) 
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:]) 
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    dious = inter_area / union - (inter_diag) / outer_diag
    dious = torch.clamp(dious,min=-1.0,max = 1.0)
    if exchange:
        dious = dious.T
    return dious

def Ciou(bboxes1, bboxes2):
    rows = bboxes1.shape[0]
    cols = bboxes2.shape[0]
    cious = torch.zeros((rows, cols))
    if rows * cols == 0:
        return cious
    exchange = False
    if bboxes1.shape[0] > bboxes2.shape[0]:
        bboxes1, bboxes2 = bboxes2, bboxes1
        cious = torch.zeros((cols, rows))
        exchange = True

    w1 = bboxes1[:, 2] - bboxes1[:, 0]
    h1 = bboxes1[:, 3] - bboxes1[:, 1]
    w2 = bboxes2[:, 2] - bboxes2[:, 0]
    h2 = bboxes2[:, 3] - bboxes2[:, 1]

    area1 = w1 * h1
    area2 = w2 * h2

    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2
    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2
    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2
    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2

    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])
    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])
    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])
    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])

    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)
    inter_area = inter[:, 0] * inter[:, 1]
    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2
    outer = torch.clamp((out_max_xy - out_min_xy), min=0)
    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)
    union = area1+area2-inter_area
    u = (inter_diag) / outer_diag
    iou = inter_area / union
    with torch.no_grad():
        arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)
        v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)
        S = 1 - iou
        alpha = v / (S + v)
        w_temp = 2 * w1
    ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)
    cious = iou - (u + alpha * ar)
    cious = torch.clamp(cious,min=-1.0,max = 1.0)
    if exchange:
        cious = cious.T
    return cious

box_1 = box1 = [0,0,8,6]
box_2 = box2 = [2,3,10,9]
print('Iou',Iou(box1, box2))
print('Giou',Giou(box1, box2))

box1 = torch.unsqueeze(torch.tensor(box1), dim = 0)
box2 = torch.unsqueeze(torch.tensor(box2), dim = 0)
print('Diou',Diou(box1, box2))
print('Ciou',Ciou(box1, box2))

---

总结