深度学习 GAN生成对抗网络-1010格式数据生成简单案例

一、前言

本文不花费大量的篇幅来推导数学公式，而是使用一个非常简单的案例来帮助我们了解GAN生成对抗网络。

二、GAN概念

生成对抗网络（Generative Adversarial Networks，GAN）包含生成器（Generator）和鉴别器（Discriminator）两个神经网络。生成器用于生成虚假的数据，经过训练后能够生成以假乱真的数据；鉴别器使用真实数据和虚假数据训练后，能够辨别数据的真假；生成器和鉴别器相互博弈，最终达到鉴别器难以区分生成数据真假的状态。

三、案例实战

我们会创建一个GAN，生成器通过学习训练，来创建符合1010格式规律的值。这个任务比生成图像要简单。通过这个任务，我们可以了解GAN的基本代码框架，观察训练进程，进而帮助我们为接下来生成图像的任务做好准备。

我们先引入依赖库：

import matplotlib.pyplot as plt
import pandas
import torch
import torch.nn as nn

2.1 构造真实数据源

真实数据源可以是一个返回1010格式数据的函数，如下所示：

def generate_real():
    real_data = torch.FloatTensor([1,0,1,0])
    return real_data

执行：

generate_real()

结果：

tensor([1., 0., 1., 0.])

但是，在实际生活中，数据往往不是那么精准，我们让其有一定随机性：

def generate_real():
    real_data = torch.FloatTensor(
        [random.uniform(0.8, 1.0),
         random.uniform(0.0, 0.2),
         random.uniform(0.8, 1.0),
         random.uniform(0.0, 0.2)])
    return real_data

random.uniform(0.8, 1.0)产生0.8-1.0之间的随机小数。
执行：

generate_real()

结果：

tensor([0.9782, 0.0673, 0.8500, 0.1788])

2.2 构造随机数据

产生4个随机数，可能满足1010格式，也可能不满足，函数如下：

def generate_random(size):
    random_data = torch.rand(size)
    return random_data

执行：

generate_random(4)

结果：

tensor([0.4241, 0.0611, 0.7684, 0.2931])

2.3 构造鉴别器

鉴别器是一个神经网络，我们的目的是训练出一个能区分真实数据与随机噪声数据的鉴别器。下面代码定义了一个非常简单的神经网络：输入层有4个节点，用于接受输入的4个值；隐藏层有3个节点；输出层输出0~1的单个值，表示真或假。

class Discriminator(nn.Module):
    
    def __init__(self):
        # 初始化Pytorch父类
        super().__init__()
        
        # 定义神经网络层
        self.model = nn.Sequential(
            nn.Linear(4, 3),
            nn.Sigmoid(),
            nn.Linear(3, 1),
            nn.Sigmoid()
        )
        
        # 创建损失函数，使用均方误差
        self.loss_function = nn.MSELoss()

        # 创建优化器，使用随机梯度下降
        self.optimiser = torch.optim.SGD(self.parameters(), lr=0.01)

        # 训练次数计数器
        self.counter = 0
        # 训练过程中损失值记录
        self.progress = []
    
    # 前向传播函数
    def forward(self, inputs):
        return self.model(inputs)
    
    # 训练函数
    def train(self, inputs, targets):
        # 前向传播，计算网络输出
        outputs = self.forward(inputs)
        
        # 计算损失值
        loss = self.loss_function(outputs, targets)

        # 累加训练次数
        self.counter += 1

        # 每10次训练记录损失值
        if (self.counter % 10 == 0):
            self.progress.append(loss.item())

        # 每10000次输出训练次数   
        if (self.counter % 10000 == 0):
            print("counter = ", self.counter)
            

        # 梯度清零, 反向传播, 更新权重
        self.optimiser.zero_grad()
        loss.backward()
        self.optimiser.step()
    
    # 绘制损失变化图
    def plot_progress(self):
        df = pandas.DataFrame(self.progress, columns=['loss'])
        df.plot(ylim=(0, 1.0), figsize=(16,8), alpha=0.1, marker='.', grid=True, yticks=(0, 0.25, 0.5))

2.4 测试鉴别器

由于还没有创建生成器，所以无法测试能够与其竞争的鉴别器，目前能做的是，检验鉴别器是否能将真实数据与随机数据区分开。

训练

D = Discriminator()
for i in range(10000):
    # 真实数据
    D.train(generate_real(), torch.FloatTensor([1.0]))
    # 随机数据
    D.train(generate_random(4), torch.FloatTensor([0.0]))

结果：

counter =  10000
counter =  20000

上述代码虽然迭代了10000次，但是在每次迭代中分别对真实数据和随机数据进行了训练，累计训练20000次。

损失值变化

我们来看看训练过程中的损失值变化：

D.plot_progress()

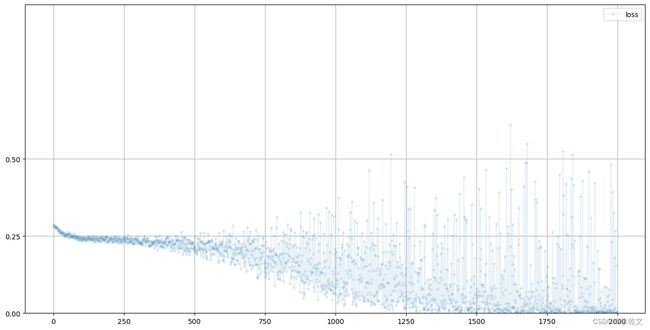
如上图所示，损失值一开始接近0.25，随着训练次数增加，损失值逐渐接近0。

鉴别效果

我们再来测试一下鉴定器的效果，现在分别输入1010格式数据与随机数据，代码和运行结果如下：

print(D.forward(generate_real()).item())
print(D.forward(generate_random(4)).item())

结果：

0.8134430050849915
0.05087679252028465

得出的结果分别接近1和0，这说明鉴别器能够区分真实数据与随机噪声。

2.5 构造生成器

生成器也是一个神经网络，目的是尽量生成满足1010格式的4个值。为了使生成器与鉴别器不相伯仲地相互竞争与提高，生成器与鉴别器的结构正好相反：输入层只有1个节点；隐藏层有3个节点；输出层有4个节点，输出4个值。
代码如下，注意训练函数稍有不同，引入了鉴别器的损失函数进行反向传播，进而更新生成器权重：

class Generator(nn.Module):
    
    def __init__(self):
        # 初始化Pytorch父类
        super().__init__()
        
        # 定义神经网络层
        self.model = nn.Sequential(
            nn.Linear(1, 3),
            nn.Sigmoid(),
            nn.Linear(3, 4),
            nn.Sigmoid()
        )

        # 注意这里没有损失函数，在训练时使用鉴别器的损失函数。

        # 创建优化器，使用随机梯度下降
        self.optimiser = torch.optim.SGD(self.parameters(), lr=0.01)

        # 训练次数计数器
        self.counter = 0
        # 训练过程中损失值记录
        self.progress = []
        
    # 前向传播函数
    def forward(self, inputs):
        return self.model(inputs)
    
    # 训练函数
    def train(self, D, inputs, targets):
        # 前向传播，计算网络输出
        g_output = self.forward(inputs)
        
        # 将生成器输出，传入鉴别器，输出分类结果
        d_output = D.forward(g_output)
        
        # 计算鉴别误差
        loss = D.loss_function(d_output, targets)

        # 累加训练次数
        self.counter += 1

        # 每10次训练记录损失值
        if (self.counter % 10 == 0):
            self.progress.append(loss.item())

        # 梯度清零, 反向传播, 更新权重。注意这里是对鉴别器的误差进行反向传播，但只更新生成器的权重
        self.optimiser.zero_grad()
        loss.backward()
        self.optimiser.step()

    # 绘制损失变化图
    def plot_progress(self):
        df = pandas.DataFrame(self.progress, columns=['loss'])
        df.plot(ylim=(0, 1.0), figsize=(16,8), alpha=0.1, marker='.', grid=True, yticks=(0, 0.25, 0.5))

2.6 检查生成器输出

同样地，我们也可以单独对生成器进行测试，以检查是否正常工作：

G = Generator()
G.forward(torch.FloatTensor([0.5]))

结果：

tensor([0.6172, 0.5979, 0.5700, 0.6622], grad_fn=)

可以看到输出了4个值，但不符合1010格式，因为我们还没有对其进行训练。

2.7 训练GAN

训练

先看代码：

D = Discriminator()
G = Generator()

for i in range(10000):
    
    # 用真实样本数据训练鉴别器
    D.train(generate_real(), torch.FloatTensor([1.0]))
    
    # 用生成数据训练鉴别器
    # 此处训练是为了更新鉴别器权重，不需要更新生成器权重，使用detach()以避免计算生成器中的梯度
    D.train(G.forward(torch.FloatTensor([0.5])).detach(), torch.FloatTensor([0.0]))
    
    # 训练生成器，更新生成器权重
    G.train(D, torch.FloatTensor([0.5]), torch.FloatTensor([1.0]))

在迭代过程中，每次循环都会重复训练GAN的3个步骤：

1. 用真实样本数据训练鉴别器，更新鉴别器权重
2. 用生成的数据训练鉴别器，更新鉴别器权重。此处不需要更新生成器权重，detach()的作用是将其从计算图中分离出来
3. 训练生成器，更新生成器权重

损失值变化

训练完成后，我们来看看鉴别器损失值的变化：

D.plot_progress()

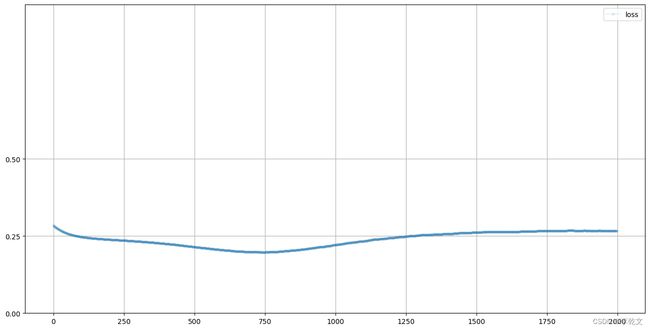
这是一个非常有意思的结果，损失值最终保持在0.25附近。这说明鉴别器无法判断数据是真实的还是伪造的，于是输出0.5，由于我们损失函数使用的是均方误差，所以损失值是0.5的平方，即0.25。

下图是生成器的损失图，与鉴别器损失是互补的：

G.plot_progress()

生成数据

现在我们用训练好的生成器来生成数据：

G.forward(torch.FloatTensor([0.5]))

结果：

tensor([0.9537, 0.0367, 0.9493, 0.0507], grad_fn=)

可以看到生成的数据符合1010格式。效果相当不错！

通过上面的训练，相信你已经熟悉GAN的结构了，后面我们将使用GAN来实现手写数字生成等更加酷炫的任务

参考资料

《PyTorch生成对抗网络编程》（PS：写得太好了，强烈推荐。）