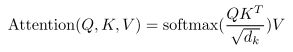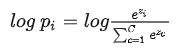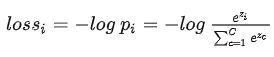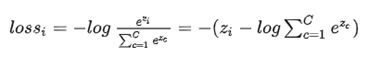论文阅读笔记:Attention is All You Need
论文标题:Attention is All You Need
目录
论文标题:Attention is All You Need
1.摘要
2.前言
3.模型结构
自注意力机制
多头自注意力机制
注意力机制在Transformer中的应用
1.摘要
过去最优的模型是带有attention连接的encoder-decoder模型,本文提出了一个名为Transformer的神经网络框架,Transformer基于注意力机制,完全不需要循环和卷积。在两个机器翻译任务上的实验表明,这些模型在质量上更高,同时更易于并行化,并且训练的时间更短。
2.前言
RNN,LSTM,GRU等模型在机器翻译上取得了优异的效果。循环语言模型沿着时间步计算,产生一个序列的隐藏状态ht。将前一个时刻的ht-1和t时刻的输入输入到模型,这种序列的设计天然地阻碍了并行训练。这在较长的序列长度时训练速度变得至关重要,因为内存限制了示例之间的批处理。
Attention允许对依赖性进行建模,而不考虑它们在输入或输出序列的距离。Self-Attention是一种注意力机制,它将单个序列的不同位置联系起来,以便计算序列的表示
基于循环注意力机制的端到端记忆网络(Encoder-Decoder with Attention),而不是序列对齐的循环,已被证明在简单的语言问答和语言建模任务中表现良好。
3.模型结构
大多数有竞争力的语言模型有encoder-decoder架构,输入为序列,表示为
输入序列
![]()
Encoder将序列转换为隐藏状态表示z
![]()
Decoder在每个时间步将隐藏状态转换输出序列
![]()
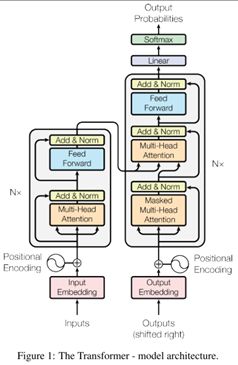
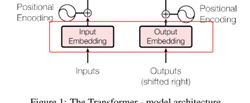
Transformer的Encoder-Decoder模块结构均为堆积的多层Self-Attention模块、全连接模块,和残差模块。其模型结构如图1,左侧为Encoder,右侧为Decoder。
Encoder: 6层网络,并在每层使用残差连接,然后进行层归一化。每层均有两个子层:多头自注意力机制,求点积的全连接层。6层网络中的每一层可以表示为,每层的隐藏层维度dmodel = 512。
![]()
Decoder: 使用相同的6层。除了每个编码器层中的两个子层之外,解码器还插入第三个子层,该子层对编码器堆积的输出执行多头注意力。Decoder每层之间用残差连接,之后使用LayerNorm。 除此之外,作者还修改了解码器中的第三个子层自注意力子层,以防止位置关注后续位置。(防止特征泄露,预测t时刻的词不应该看到Enocder中t+1之后的特征),作者使用了mask机制。
![]()
灰色部分为i位置之后的mask
Mask的解释:想让当前decoder layer的每一个位置,能处理上一层decode layer的每一个位置。但为了不发生信息穿越,decoder layer做self-attention时,不应该注意到自己之后的位置(因为自己之后的位置此时并没有输出任何东西)。
具体做法是,直接把蒙版区的attention矩阵的值设为负无穷。表示对该区域的注意力为负无穷! Softmax之后对应区域的权重会趋向于0。
注意,置为负无穷发生在softmax之前。
参考:https://blog.csdn.net/w55100/article/details/94460352
自注意力机制
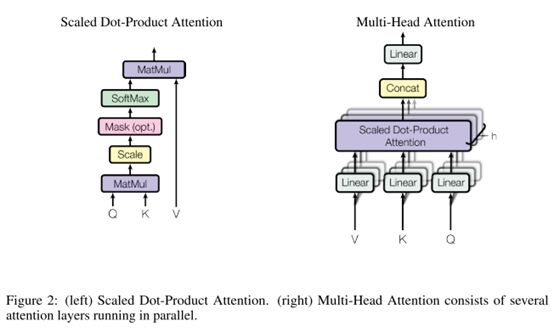
图2中左图为标度点积注意力,右图为并行的多图注意力。自注意力机制以序列的每个词特征作为输入,将每个词乘以WQ、Wk、Wv三个权重矩阵,这样做的目的是为了增强模型的表达能力。得到Q(查询向量)、K(key匹配向量)、V(Value值向量);在得到每个词的Q\K\V表示后,就可以取计算词与词之间的自注意力机制。
什么是自注意力机制?
计算每个词i与其他词j之间的权重αij,然后用αij乘以对应的值向量Vj, 得到词i的加权表示。文中使用的是矩阵乘法的形式
![]()
使用1√d 的目的是做归一化,d是的向量维度。在点积之后,qk得到的是一个标量,q与所有k的点积可以形成一个向量,随着d维度的增加,这里有些qk对的点积会非常大,而有些会很小,一个向量中的数据分布是不均匀的。
经过softmax之后,会把qk点积大的维度进一步放大,计算的数值也会变得非常大,数值可能溢出。而qk点积小的缩小,对于qk点小的维度softmax之后会出现梯度消失。
因此,使用1√d将q,k向量的点积分布做归一化,将数据的分布差异缩小,抵消softmax梯度消失现象。
Softmax函数:一文详解Softmax函数 - 知乎
https://zhuanlan.zhihu.com/p/41571249
SoftMax函数的输出,加上log不影响函数的单调性,为pi添加log运算
Pi正确类别对应的输出节点的概率,我们希望pi越大越好(0 进一步处理得到SoftMax损失函数 交叉熵损失(由极大似然推导得到) 作者发现将查询q,键k和值v用不同的线性变化k次到dq,dk,dv是有益的。然后再h组q,k,v上并行地执行自注意力函数,产生dv维度的值向量,将h个dv维度的值向量进行拼接,然后做线性变化,得到最终的值向量。 多头注意力允许模型注意到不同位置的不同表示的子空间。文中使用8(h=8)个自注意力头,每个注意力头将q,k,v映射到dq\dk\dv=64 FNN(x) = Max(0,W1Z+B)W2 + b2 参数共享, encoder的input Embeddings和Decoder的input Embedding、以及pre-softmax线性变化这三部分共享参数 这三部分为什么要做参数共享? (1)三部分参数的形状是一致的 (2)Encoder和Decoder的embedding, 输入的此表相同(机器翻译) (3)对于pre-softmax层,直接利用embd里训练出来的相似性,可以提高softmax的表现 位置编码 Transformer不包含循环神经单元和卷积单元,为了利用位置信息,必须添加一些句子中token的相对位置和绝对位置信息。在Encoder和Decoder的input embedding处添加了位置编码信息,位置编码和嵌入的维度相同,都为dmodel, 直接两者相加。 文中使用了正弦和余弦函数做词的位置编码 为什么通过正弦和余弦函数就可以表示所有词的位置编码? 每个token的位置都是一个维度为dmoel的一维向量,做位置编码时用到了特征的信息 [sin(pos/10000^2i/1), sin(pos/10000^2i/2),…, sin(pos/10000^2i/dmodel)] 那么pos+k位置的向量, PE_{pos+k} = [sin((pos+k)/a^h(0))...,sin((pos+k)/a^h(i)),...] Sin(a+b) = sin(a)cos(b)+sin(b)cos(a), 那么pos+k位置的向量, PE_{pos+k}相当于 u*sin(a)+v*cos(a),其中sin(a) = PE_pos,cos(a)= sqrt(1-PE_pos^2)。 文章使用sin-cos的位置编码的原因: (1)使用自学习position encoding的效果与正弦余弦函数几乎一样 (2)使用正弦曲线可以让模型推断的序列长度大于训练时给定的长度 参考阅读: https://blog.csdn.net/changreal/article/details/102630873多头自注意力机制
注意力机制在Transformer中的应用