数学建模——拟合

一、数据拟合方法

1.1多项式拟合

（1）拟合指令

polyift(X,Y,N);多项式拟合，返回降幂排列的多项式系数

polyval(P,xi):计算多项式的值

拟合示例：

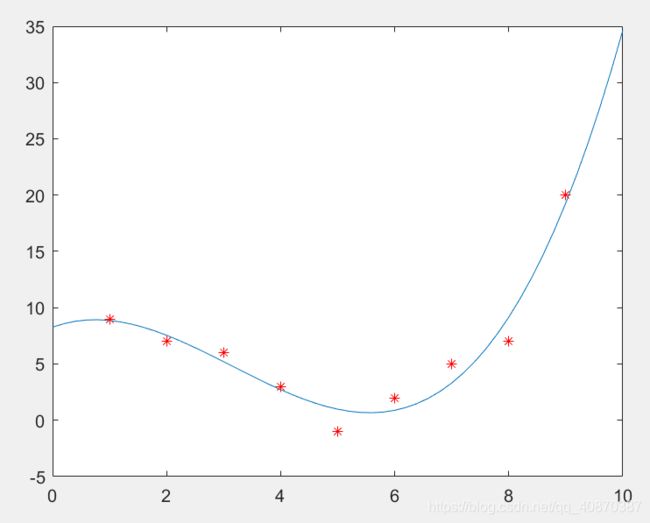
 x = [1 2 3 4 5 6 7 8 9];
 y = [9 7 6 3 -1 2 5 7 20];
 P = polyfit(x,y,3);
 xi = 0:.2:10;
 yi = polyval(P,xi);
 plot(xi,yi,x,y,'r*');

 （2）图形窗口多项式拟合

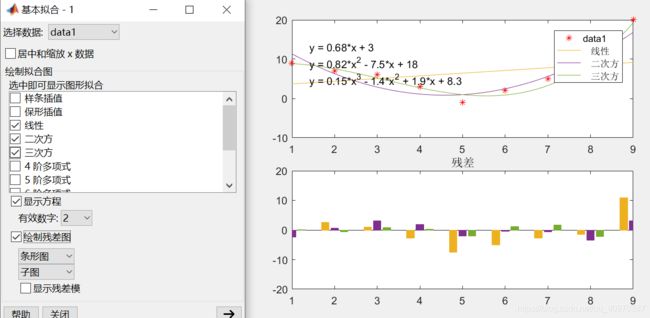
x = [1 2 3 4 5 6 7 8 9];
y = [9 7 6 3 -1 2 5 7 20];
plot(x,y,'r*');

然后在图形窗口单击 工具——基本拟合，选用线性、二次项、三次项进行拟合。

1.2指定函数拟合

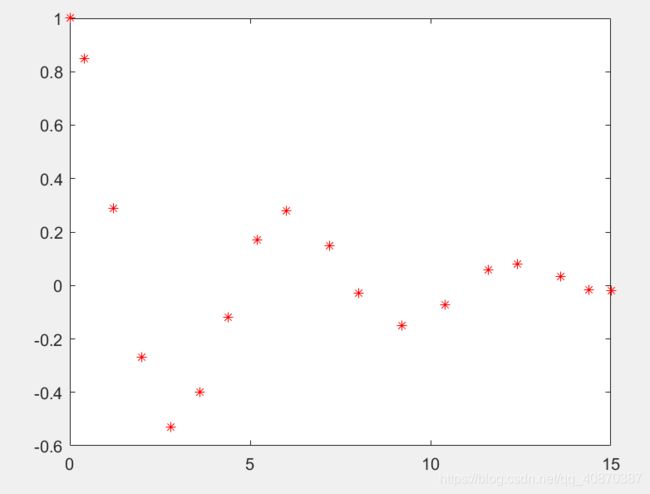
原始数据

编写m文件

 syms t
 x = [0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];
 y = [1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02];
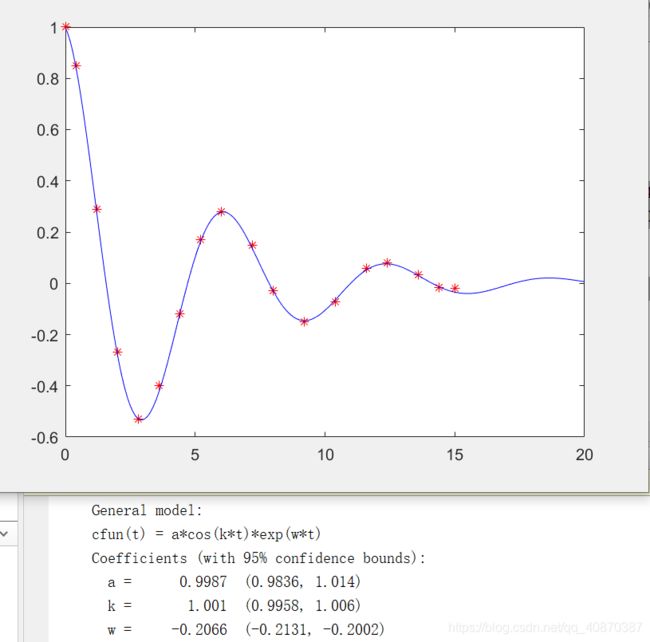
 f = fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});
 cfun = fit(x,y,f)    %显示拟合函数
 xi = 0:.1:20;
 yi = cfun(xi);
 plot(x,y,'r*',xi,yi,'b-');

程序中，函数fittype是自定义拟合函数；cfun=fit(x,y,f)根据自定义的拟合函数f来拟合数据x,y。

1.3曲线拟合工具箱

在控制台直接输入cftool命令

二、数据拟合实例

2.1人口预测模型

表中是某地区1971——2000年的人口数据，试给出该地区人口增长的数学模型。

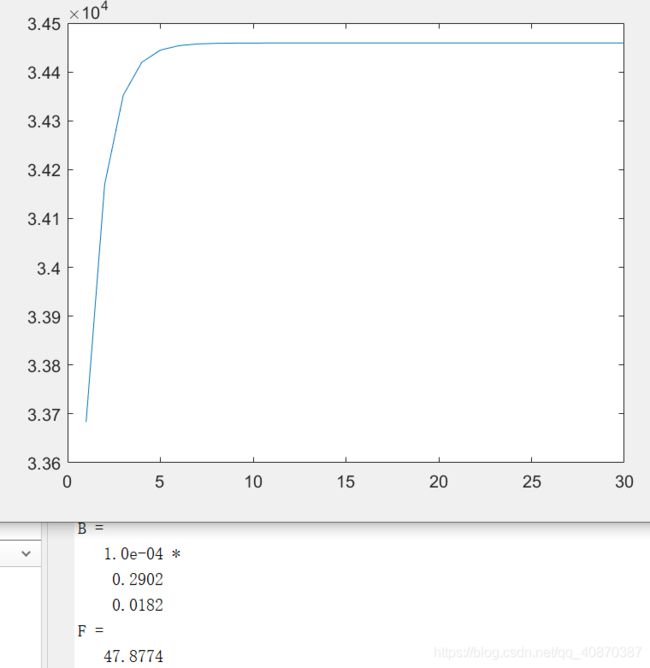
首先给出人口数据的散点图

       从图中可以看出，人口随时间的变化呈非线性过程，而且存在一个与横坐标轴平行的渐近线，故可用Logistic曲线模型进行拟合。

% 读入人口数据（1971-2000）
Y = [33815 33981 34004 34165 34212 34327 34344 34458 34498 34476 34483 34488 34513 34497 34511 34520 34507 34509 34521 34513 34515 34517 34519 34519 34521 34521 34523 34525 34525 34527];
% 读入时间变量数据（t = 年份-1970）
T = [1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30];
plot(T,Y,'r*')
% 线性化处理
for t = 1:30,
    x(t) = exp(-t);
    y(t) = 1/Y(t);
end
% 计算，并输出回归系数B
c = zeros(30,1)+1;
X = [c,x'];
B = inv(X'*X)*X'*y'
for i=1:30,
    % 计算回归拟合值
    z(i) = B(1,1)+B(2,1)*x(i);
    % 计算离差
    s(i) = y(i) - sum(y)/30;
    % 计算误差
    w(i) = z(i) - y(i);
end
% 计算离差平方和S
S = s*s';
% 回归误差平方和Q
Q = w*w';
% 计算回归平方和U
U = S-Q;
% 计算，并输出F检验值
F= 28*U/Q
% 计算非线性回归模型的拟合值
for j=1:30,
    Y(j) = 1/(B(1,1)+B(2,1)*exp(-j));
end
%输出非线性回归模型的拟合曲线
plot(T,Y)

2.2薄膜渗透率测定

三、数据可视化

地形地貌图的绘制

首先是要将未测量地点的高度用数据插值的方法求出来，然后就可以用MATLABA绘图方法画出地貌图。

[x,y] = meshgrid(1:10);                             %构造测量网络
h = [0,0.02,-0.12,0,-2.09,0,-0.58,-0.08,0,0;
    0.02,0,0,-2.38,0,-4.96,0,0,0,-0.1;
    0,0.1,1,0,-3.04,0,-0.53,0,0.1,0;
    0,0,0,3.52,0,0,0,0,0,0;
    -0.43,-1.98,0,0,0,0.77,0,2.17,0,0;
    0,0,-2.29,0,0.69,0,2.59,0,0.3,0;
    -0.09,-0.31,0,0,0,4.27,0,0,0,-0.01;
    0,0,0,5.13,7.4,0,1.89,0,0.04,0;
    0.1,0,0.58,0,0,1.75,0,-0.11,0,0;
    0,-0.01,0,0,0.3,0,0,0,0,0.01];                  %测量数据点
[xi,yi] = meshgrid(1:0.1:10);                       %构造插值网络
hi = interp2(x,y,h,xi,yi,'spline');                 %二维插值命令
surf(hi);                                           %画出地貌图
xlabel('x'),ylabel('y'),zlabel('h');                %添加坐标名称