【MR】几何雅可比vs解析雅可比 + python加载Indy7的URDF逆动力学仿真(MR+Pybullet)对比...
Python加载urdf解析为MR参数,Pybullet加载urdf,逆动力学仿真
知识点:
几何雅可比,就是关节空间速度映射到末端的空间速度
解析雅可比,就是不同姿态表示下所求的导数,比如欧拉角表示法,用来表示末端姿态的变化,通过末端欧拉角速度向角速度的转换,需要通过一个雅可比矩阵来完成
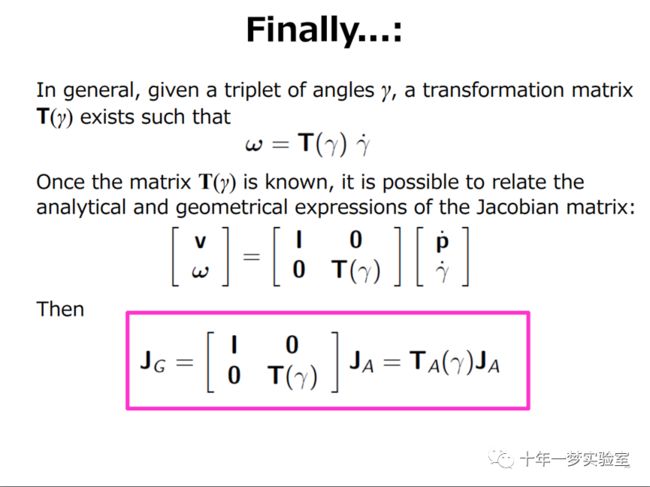
解析雅可比与几何雅可比关系的推导:
Python加载URDF解析为MR参数:(含解析雅可比计算)
from urdfpy import URDF
import numpy as np
import modern_robotics as mr
def TransformToXYZ(T):
return np.array(T[0:3,3])
def getJoint(robot,link_name):
ret_link=[]
for link in robot.links:
if link.name == link_name:
ret_link=link
break;
return ret_link
def w_p_to_Slist(w,p,ROBOT_DOF):
Slist = []
for i in range(0,ROBOT_DOF):
w_ = w[i];
p_ = p[i];
v_ = -np.cross(w_,p_)
Slist.append([w_[0],w_[1],w_[2],v_[0],v_[1],v_[2]])
return np.transpose(Slist)
#几何雅可比转解析雅可比-后增加
def analyticaljacobian(M,Blist, thetalist):
Jb = mr.JacobianBody(Blist, thetalist)
Tsb = mr.FKinBody(M,Blist, thetalist)
Ajacobian = np.vstack(
(np.hstack((np.identity(3), np.zeros((3, 3)))),
np.hstack((np.zeros((3, 3)), np.linalg.inv(Tsb[0:3,0:3]))))
).dot(Jb)
return Ajacobian
#原版本
def AnalyticJacobianBody(M,Blist, thetalist):
"""Computes the Analytic Jacobian for an open chain robot
:param Blist: The joint screw axes in the end-effector frame when the
manipulator is at the home position, in the format of a
matrix with axes as the columns
:param thetalist: A list of joint coordinates
:return: The body Jacobian corresponding to the inputs (6xn real
numbers)
Example Input:
Blist = np.array([[0, 0, 1, 0, 0.2, 0.2],
[1, 0, 0, 2, 0, 3],
[0, 1, 0, 0, 2, 1],
[1, 0, 0, 0.2, 0.3, 0.4]]).T
thetalist = np.array([0.2, 1.1, 0.1, 1.2])
Output:
np.array([[-0.04528405, 0.99500417, 0, 1]
[ 0.74359313, 0.09304865, 0.36235775, 0]
[-0.66709716, 0.03617541, -0.93203909, 0]
[ 2.32586047, 1.66809, 0.56410831, 0.2]
[-1.44321167, 2.94561275, 1.43306521, 0.3]
[-2.06639565, 1.82881722, -1.58868628, 0.4]])
"""
Jb = mr.JacobianBody(Blist, thetalist)
Tsb = mr.FKinBody(M,Blist, thetalist)
Rsb= Tsb[0:3,0:3]
#r = mr.so3ToVec(Rsb) #SO3 这里有问题 应为 ?mr.so3ToVec(MatrixLog3(Rsb))
#norm_r = np.sqrt(r[0]*r[0]+r[1]*r[1]+r[2]*r[2])
#omega_r = mr.VecToso3(r) #转轴矢量的so3
#A = np.eye(3) - (1-np.cos(norm_r))/(norm_r*norm_r) * omega_r+ (norm_r - np.sin(norm_r)) / (norm_r**3) * omega_r @ omega_r
A_ = np.eye(6)
A_[0:3,0:3] = Rsb
A_[3:6,3:6] = Rsb
Ja = A_ @ Jb
return Ja
def loadURDF(urdf_name):
print(urdf_name)
robot = URDF.load(urdf_name)
LinkNum = len(robot.links)
JointNum = len(robot.actuated_joints)
p_ = []
w_= []
M_list = [np.eye(4)]
Glist =[]
com_p_=[]
for joint in robot.actuated_joints:
child_link = getJoint(robot,joint.child)
p_.append(TransformToXYZ(robot.link_fk()[child_link]))
G = np.eye(6)
G[0:3,0:3] = child_link.inertial.inertia
G[3:6,3:6] = child_link.inertial.mass*np.eye(3)
Glist.append(G)
child_M = robot.link_fk()[child_link]
child_M_R, child_M_p =mr.TransToRp(child_M)
child_w = np.array(child_M_R @ np.array(joint.axis).T)
w_.append( child_w )
child_M[0:3,0:3] = np.eye(3)
CoM_M = child_M@ child_link.inertial.origin
M_list.append(CoM_M)
eef_link = getJoint(robot,robot.end_links[0].name)#获取末端连杆的关节
M = robot.link_fk()[eef_link]
M_list.append(M)
Slist = w_p_to_Slist(w_,p_,JointNum)
Blist = mr.Adjoint(mr.TransInv(M))@ Slist
Mlist = []
for i in range(1,len(M_list)):
M_i_1 = M_list[i-1]
M_i = M_list[i]
Mlist.append(mr.TransInv(M_i_1) @ M_i)
Mlist = np.array(Mlist)
Glist = np.array(Glist)
return {"M":M,"Slist" : Slist,"Blist": Blist,"Mlist":Mlist,"Glist":Glist,"actuated_joints_num":len(robot.actuated_joints)}indy7_sim.p(Pybullet与MR逆动力学仿真对比)
import pybullet as p
import time
import pybullet_data
import numpy as np
np.set_printoptions(precision=6, suppress=True)
import math
from modern_robotics import *
import modern_robotics as mr
import numpy as np
from mr_urdf_loader import loadURDF
from mr_urdf_loader import *
def pos_orn_to_T(pos,orn):
T = np.eye(4)
T[0:3,3] = np.array(pos).T
T[0:3,0:3] = np.reshape(p.getMatrixFromQuaternion(orn),(3,3))
return T
#几何雅可比转解析雅可比 与
def analyticaljacobian(M,Blist, thetalist):
Jb = mr.JacobianBody(Blist, thetalist)
Tsb = mr.FKinBody(M,Blist, thetalist)
Ajacobian = np.vstack(
(np.hstack((np.identity(3), np.zeros((3, 3)))),
np.hstack((np.zeros((3, 3)), np.linalg.inv(Tsb[0:3,0:3]))))
).dot(Jb)
return Ajacobian
urdf_name = "V:/learn/MR/download/mr_urdf_loader-main/example/indy7/indy7/indy7.urdf"
## Modern Robotics setup
MR=loadURDF(urdf_name)
M = MR["M"]
Slist = MR["Slist"]
Mlist = MR["Mlist"]
Glist = MR["Glist"]
Blist = MR["Blist"]
actuated_joints_num = MR["actuated_joints_num"]
## pybullet setup
p.connect(p.GUI)
p.setGravity(0, 0, -9.8)
p.setAdditionalSearchPath(pybullet_data.getDataPath())
robotID = p.loadURDF(urdf_name, [0, 0, 0],[0, 0, 0, 1],useFixedBase=1)
numJoints = p.getNumJoints(robotID)
p.resetBasePositionAndOrientation(robotID, [0, 0, 0], [0, 0, 0, 1])
for i in range(0,numJoints):
p.setJointMotorControl2(robotID, i, p.VELOCITY_CONTROL, targetVelocity=0, force=0)
#p.resetJointState(robotID,2,1) 无明显变化
useRealTimeSim = False
p.setRealTimeSimulation(useRealTimeSim)
timeStep = 1/240.0;
p.setTimeStep(timeStep)
q = [0,0,0,0,0,0] #q = [0,0,0,0,0,0]
q_dot = [0,0,0,0,0,0]#[0,0,0,0,0,0]
q_ddot = [0,1,0,0,0,0]
g = np.array([0,0,-9.8])
Ftip = [0,0,0,0,0,0]
print(Glist[0][0:3,0:3])
print(Glist[1][0:3,0:3])
print(Glist[2][0:3,0:3])
print(Glist[3][0:3,0:3])
''' print(Glist[4][0:3,0:3])
print(Glist[5][0:3,0:3]) '''
print(p.getDynamicsInfo(robotID, 1)[2]) #主惯性矩
print(p.getDynamicsInfo(robotID, 2)[2])
print(p.getDynamicsInfo(robotID, 3)[2])
print(p.getDynamicsInfo(robotID, 4)[2])
while p.isConnected():
# get Joint Staes
jointStates = np.array(p.getJointStates(robotID,[1,2,3,4,5,6]),dtype=object)
# get Link Staes
linkState = np.array(p.getLinkState(robotID,7,1,1),dtype=object)
q = np.array(jointStates[:,0])
q_dot = np.array(jointStates[:,1])
# Pybullet Forward Kinematics
pb_Tsb = pos_orn_to_T(linkState[0],linkState[1])
# Modern Robotics Forward Kinematics
mr_Tsb = mr.FKinSpace(M,Slist,q)
mr_Tsb = mr.FKinBody(M,Blist,q)
# Pybullet Jacobian
#pb_J = p.calculateJacobian(robotID,4,[0,0,0],[q[0],q[1],q[2]],[q_dot[0],q_dot[1],q_dot[2]],[0,0,0])
# Modern Robotics Jacobian
mr_Jb= JacobianBody(Blist, q)
mr_Js= JacobianSpace(Slist, q)
#mr_ja mr_ja2 结果一样
mr_Ja = AnalyticJacobianBody(M,Blist, q) # pb_j = mr_Ja
mr_Ja2=analyticaljacobian(M,Blist, q)
#print("=============mr_Ja=============")
#print(mr_Ja)
#print("=============mr_Ja2=============")
#print(mr_Ja2)
#pybullet InverseDynamics
print(q)
pb_ID= np.array(p.calculateInverseDynamics(robotID,[q[0],q[1],q[2],q[3],q[4],q[5] ],[q_dot[0],q_dot[1],q_dot[2],q_dot[3],q_dot[4],q_dot[5] ] ,[0,0,0,0,0,0] ))
#modern_robotics InverseDynamics
mr_ID =mr.InverseDynamics(q, q_dot, q_ddot, g, Ftip, Mlist, Glist, Slist)
print("=============pb_Tsb=============")
print(pb_Tsb)
print("=============mr_Tsb=============")
print(mr_Tsb)
print("=============pb_ID=============")
print(pb_ID)
print("=============mr_ID=============")
print(mr_ID)
#set torques
for i in range(0,actuated_joints_num):
p.setJointMotorControl2(robotID, i+1, p.TORQUE_CONTROL,force=mr_ID[i])
#p.setJointMotorControl2(robotID, i+1, p.TORQUE_CONTROL,force=pb_ID[i])
p.stepSimulation()
time.sleep(timeStep)indy7_urdf_loader.py测试加载urdf解析为MR参数程序
import numpy as np
np.set_printoptions(precision=6, suppress=True)
from mr_urdf_loader import loadURDF
from modern_robotics import *
urdf_name = "V:/learn/MR/download/mr_urdf_loader-main/example/indy7/indy7/indy7.urdf"
MR=loadURDF(urdf_name)
M = np.array(MR["M"])
Slist = np.array(MR["Slist"])
Mlist = np.array(MR["Mlist"])
Glist = np.array(MR["Glist"])
Blist = np.array(MR["Blist"])
actuated_joints_num = MR["actuated_joints_num"]
thetalist = np.array([0,0,np.pi/2.0])
dthetalist = np.array([0,0,0.1])
ddthetalist = np.array([0,0,0])
g = np.array([0,0,-9.8])
Ftip = [0,0,0,0,0,0]
#print(M)
print(Mlist)
print(Glist)
print("FKinSpace\n", FKinSpace(M,Slist,thetalist))
print("FKinBody\n", FKinBody(M,Blist,thetalist))
print("JacobianSpace\n", JacobianSpace(Slist,thetalist))
print("JacobianBody\n", JacobianBody(Blist,thetalist))
print("InverseDynamics\n" ,InverseDynamics(thetalist, dthetalist, ddthetalist, g, Ftip, Mlist, Glist, Slist))测试加载URDF解析为MR参数程序的输出:
PS V:\learn\MR\download\mr_urdf_loader-main> v:; cd 'v:\learn\MR\download\mr_urdf_loader-main'; & 'C:\Users\cxy\AppData\Local\Programs\Python\Python39\python.exe' 'c:\Users\cxy\.vscode\extensions\ms-python.python-2022.16.1\pythonFiles\lib\python\debugpy\adapter/../..\debugpy\launcher' '63759' '--' 'v:\learn\MR\download\mr_urdf_loader-main\example\indy7\indy7_urdf_loader.py'
V:/learn/MR/download/mr_urdf_loader-main/example/indy7/indy7/indy7.urdf
[[[ 1. 0. 0. 0. ]
[ 0. 1. 0. 0. ]
[ 0. 0. 1. 0.0775]
[ 0. 0. 0. 1. ]]
[[ 1. 0. 0. 0. ]
[ 0. 1. 0. -0.109 ]
[ 0. 0. 1. 0.222 ]
[ 0. 0. 0. 1. ]]
[[ 1. 0. 0. -0. ]
[ 0. 1. 0. 0.0305]
[ 0. 0. 1. 0.45 ]
[ 0. 0. 0. 1. ]]
[[ 1. 0. 0. -0. ]
[ 0. 1. 0. 0.075 ]
[ 0. 0. 1. 0.267 ]
[ 0. 0. 0. 1. ]]
[[ 1. 0. 0. 0. ]
[ 0. 1. 0. -0.114 ]
[ 0. 0. 1. 0.083 ]
[ 0. 0. 0. 1. ]]
[[ 1. 0. 0. -0. ]
[ 0. 1. 0. -0.069 ]
[ 0. 0. 1. 0.168 ]
[ 0. 0. 0. 1. ]]
[[ 1. -0. 0. 0. ]
[ 0. 1. -0. -0. ]
[ 0. 0. 1. 0.06 ]
[ 0. 0. 0. 1. ]]]
[[[ 0.154186 -0.000002 0.000017 0. 0. 0. ]
[-0.000002 0.12937 -0.048543 0. 0. 0. ]
[ 0.000017 -0.048543 0.059644 0. 0. 0. ]
[ 0. 0. 0. 11.80301 0. 0. ]
[ 0. 0. 0. 0. 11.80301 0. ]
[ 0. 0. 0. 0. 0. 11.80301 ]]
[[ 0.29357 -0. 0.000014 0. 0. 0. ]
[-0. 0.280941 0.03728 0. 0. 0. ]
[ 0.000014 0.03728 0.036206 0. 0. 0. ]
[ 0. 0. 0. 7.992921 0. 0. ]
[ 0. 0. 0. 0. 7.992921 0. ]
[ 0. 0. 0. 0. 0. 7.992921]]
[[ 0.034246 0.000001 0.000007 0. 0. 0. ]
[ 0.000001 0.03406 0.00186 0. 0. 0. ]
[ 0.000007 0.00186 0.004505 0. 0. 0. ]
[ 0. 0. 0. 2.991341 0. 0. ]
[ 0. 0. 0. 0. 2.991341 0. ]
[ 0. 0. 0. 0. 0. 2.991341]]
[[ 0.006704 0.000004 0.000002 0. 0. 0. ]
[ 0.000004 0.002792 -0.00128 0. 0. 0. ]
[ 0.000002 -0.00128 0.006193 0. 0. 0. ]
[ 0. 0. 0. 2.12317 0. 0. ]
[ 0. 0. 0. 0. 2.12317 0. ]
[ 0. 0. 0. 0. 0. 2.12317 ]]
[[ 0.009949 0. 0.000003 0. 0. 0. ]
[ 0. 0.009782 -0.000935 0. 0. 0. ]
[ 0.000003 -0.000935 0.002715 0. 0. 0. ]
[ 0. 0. 0. 2.288651 0. 0. ]
[ 0. 0. 0. 0. 2.288651 0. ]
[ 0. 0. 0. 0. 0. 2.288651]]
[[ 0.000435 0. -0. 0. 0. 0. ]
[ 0. 0.000445 0.000001 0. 0. 0. ]
[-0. 0.000001 0.000596 0. 0. 0. ]
[ 0. 0. 0. 0.400839 0. 0. ]
[ 0. 0. 0. 0. 0.400839 0. ]
[ 0. 0. 0. 0. 0. 0.400839]]]
FKinSpace
[[ 0. -0. -1. -0.578 ]
[ 0. 1. -0. -0.1865]
[ 1. -0. 0. 0.7495]
[ 0. 0. 0. 1. ]]
FKinBody
[[ 0. -0. -1. -0.578 ]
[ 0. 1. -0. -0.1865]
[ 1. -0. 0. 0.7495]
[ 0. 0. 0. 1. ]]
JacobianSpace
[[ 0. 0. 0. 0. 0. 0. ]
[ 0. -1. -1. -0. -1. -0. ]
[ 1. 0. 0. 1. -0. 1. ]
[-0. 0.2995 0.7495 -0.0035 1.0995 -0.1865]
[-0. 0. 0. 0. 0. 0. ]
[-0. 0. 0. 0. 0. 0. ]]
JacobianBody
[[ 1. -0. -0. 0. -0. 0. ]
[-0. -1. -1. 0. -1. 0. ]
[ 0. 0. 0. 1. 0. 1. ]
[-0. -0.578 -0.578 0.183 -0.228 0. ]
[-0.578 0. 0. -0. -0. -0. ]
[-0.1865 0.45 -0. 0. -0. -0. ]]
InverseDynamics
[ 0.000019 -0. 0. ]