JXNU20级第六次周练题解
niconiconi
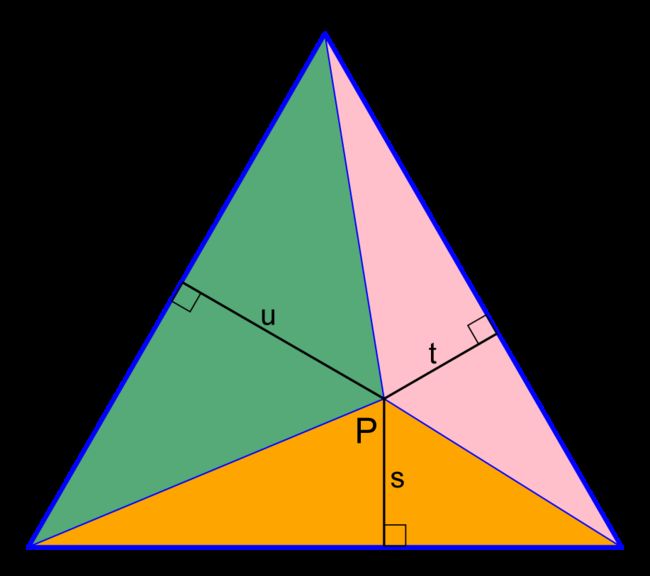
三角形面积 S = ( A B ∗ s + B C ∗ t + A C ∗ u ) / 2 = A B ∗ h / 2 S = (AB * s + BC * t + AC * u)/2 = AB * h / 2 S=(AB∗s+BC∗t+AC∗u)/2=AB∗h/2 (h为三角形在AB边上的高)
因为这是等边三角形,所以 s + t + u = h = 3 ∗ A B / 2 s+t+u = h = \sqrt3 * AB / 2 s+t+u=h=3∗AB/2
#include奶茶加珍珠
因为奶茶最便宜的都要2元,而珍珠的价格也是2元,而加第一份珍珠相当于2元买了同样的一杯奶茶,而第二份珍珠相当与2元买了2杯奶茶,所以肯定不会买两杯奶茶,只需要买一杯奶茶,剩下的钱全部加珍珠就能得到最大的满足感
#include朝阳摆花
要想丑陋度最小,按照顺时针摆花 花的高度应该先上升后下降;当然先下降后上升也行
用数组表示既为数组是先上升后下降的,数组最后一个元素和第一个元素相邻
先假设花的高度为 [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ] [1,2,3,4,5,6,7,8] [1,2,3,4,5,6,7,8]
先摆放高度为1的花 序列为 [ 1 , n u l l , n u l l , n u l l , n u l l , n u l l , n u l l , n u l l ] [1,null,null,null,null,null,null,null] [1,null,null,null,null,null,null,null] null表示该位置没有摆放花
然后把2和3摆放到nul的最左端和最右端,得到 [ 1 , 2 , n u l l , n u l l , n u l l , n u l l , n u l l , 3 ] [1,2,null,null,null,null,null, 3] [1,2,null,null,null,null,null,3]
接下来依次摆放高度为4和5的花 [ 1 , 2 , 4 , n u l l , n u l l , n u l l , 5 , 3 ] [1,2,4,null,null,null,5, 3] [1,2,4,null,null,null,5,3]
然后再摆放高度为6和7的花 [ 1 , 2 , 4 , 6 , n u l l , 7 , 5 , 3 ] [1,2,4,6,null,7,5, 3] [1,2,4,6,null,7,5,3]
最后摆放高度为8的花 [ 1 , 2 , 4 , 6 , 8 , 7 , 5 , 3 ] [1,2,4,6,8,7,5, 3] [1,2,4,6,8,7,5,3]
因为某朵花 a i a_i ai 要与两朵花 a i + 2 a_{i+2} ai+2 和 a i − 2 a_{i-2} ai−2 相邻,所以可以对排序后的花隔一个遍历,计算它们高度差的最大值。
注意当 n = 2 n = 2 n=2时,只有两朵花,直接计算它们的高度差。
#include朝阳爱奇数
把所有偶数除2一直除到奇数,统计次数即可
#include拯救雪乃酱
一个文本的输入,一个字母的输出,可以一直处理到文件结尾。接下来统计计数即可。
#include财政报告
注意观察输入范围 [ 1 , 2 64 ) [1,2^{64}) [1,264),出这个题目的目的就是让做题人真实掌握 c / c p p c/cpp c/cpp中数据类型的数据范围。一个字节存在八个二进制位。但是注意可能存在一个符号位,带 u n s i g n e d unsigned unsigned前缀的数据类型才不存在符号位。
- char 1字节 [ − 2 7 , 2 7 − 1 ] [-2^7,2^7-1] [−27,27−1]
- bool 1字节 [ 0 , 1 ] [0,1] [0,1]
- int 4字节 [ − 2 31 , 2 31 − 1 ] [-2^{31},2^{31}-1] [−231,231−1]
- unsigned int 4字节 [ 0 , 2 32 − 1 ] [0,2^{32}-1] [0,232−1]
- double 8字节
- long long 8字节 [ − 2 63 , 2 63 − 1 ] [-2^{63},2^{63}-1] [−263,263−1]
- unsigned long long 8字节 [ 0 , 2 64 − 1 ] [0,2^{64}-1] [0,264−1]
算法竞赛中基本需要的都被列举在上方,有几个建议,有关浮点数统一使用 double,当 double 精度都不够的时候使用 long double,整数输入以及计算的时候,自己时刻需要清醒的判断是否会溢出int,如果溢出需要转成 long long 去计算,涉及 1 e 9 + 7 1e9+7 1e9+7取模的时候也是需要先开 long long 计算。
回到这个题目,看到数据范围,使用 unsigned long long 就可以保存下去,不需要开大数去模拟。
使用变量保存之后,因为涉及 a − b a-b a−b操作,在无符号变量做减法时,需要小心,因为它不能计算到正确的负数答案。所以我们只需要判断一下 a , b a,b a,b大小是否需要输出负号,这个题目就写完了。
#include 队员的能力值
本题目的就是为了让你们学会计数排序。本题时间被我精心设计了,只能在时间复杂度 O ( n ) O(n) O(n)的情况下才能不超时。也就是卡掉了使用快速排序 s o r t ( ) sort() sort()方法。
本题的 n ≤ 1300000 n\leq1300000 n≤1300000,但是 a i ≤ 50 a_i\leq50 ai≤50,我们使用一个 c n t cnt cnt数组统计其中每个数字出现过几次。
接下来是不是只需要把 c n t cnt cnt数组从 1 1 1到 50 50 50全部遍历一遍就可以输出从小到大的序列了。
#include 解方程
首先不考虑任何优化的前提下使用三重循环依次判断时间复杂度 O ( n 3 ) O(n^3) O(n3)。
这个在 n ≤ 1000 n\leq1000 n≤1000时,最坏情况下需要枚举的循环次数达到了 1 e 9 1e9 1e9的规模。这在 1 1 1s的时间是不可能完成的。特别还有多组输入的情况。
1 1 1s的时间限制,极限的循环次数应该也就是 1 e 8 1e8 1e8了。但是也尽量不要达到这个规模,考虑优化自己的算法,因为当你的算法常数比较大的时候,也是会超时的。
回来这个题目尽量三重循环不行,我们能不能优化掉一层循环,我们最后还需要枚举最后一个数嘛?是不是固定前面两个最后一个数也就与之固定了呢?答案是肯定的。
那么我们就可以使用二分查找去数组中找那个符合的答案。但是二分查找前提是数组有序。排序的时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn),在使用快速排序的前提下,后面两层循环+二分查找的时间复杂度 O ( n 2 l o g n ) O(n^2logn) O(n2logn)。
很显然整个算法的时间复杂度就是 O ( n 2 l o g n ) O(n^2logn) O(n2logn)了,所以说使用冒泡排序也可以通过。
方案一:标准的c语言版
#include 方案一:cpp进阶版
#include 还有一种。使用一个很大的桶,保证可以记录出现过的 c c c。这样我们就省略掉二分查找这个步骤,直接看桶中是否存在这个解。还有一个要注意的点就是,数组下标不能出现负数,所以我们需要使用整体后推的办法。也就是把 − 1000 -1000 −1000看作 0 0 0,把 0 0 0看作 1000 1000 1000,把 1000 1000 1000看作 2000 2000 2000去判断。这样就可以直接通过下标索引判断真假而找到答案。
这种做法时间复杂度 O ( n 2 ) O(n^2) O(n2),但是需要多开空间去标记。牺牲空间换时间。当 n ≤ 5000 n\leq5000 n≤5000时使用上方的做法就可能会超时了,需要掌握这种桶标记的方案。
方案二:桶标记法
#include快发奖金!
首先先看每个人需要的金钱是不会改变的,那么这个题目题意翻译就是每一个点权值是恒定不变的,你需要查找区间 [ l , r ] [l,r] [l,r]的和。
接下来就要解释一个算法知识点了,叫做前缀和。
如果我需要查询 T T T次,每次都查询 [ 1 , n ] [1,n] [1,n]的和,如果每次你都从头算,那么需要算 T ∗ n T*n T∗n次,而且非常非常多的重复计算,当这个 T , n T,n T,n比较大的时候就会超时。
使用一个数组 s u m sum sum,如果原来数组是 a a a。那么我们规定, s u m i = ∑ j = 1 j = i a j sum_i = \sum_{j=1}^{j=i}a_j sumi=∑j=1j=iaj。
那么如果我们需要查找区间 [ l , r ] [l,r] [l,r]的和,那么对应的就是 s u m r − s u m l − 1 sum_r-sum_{l-1} sumr−suml−1。
再来看这个题目,也就是前缀和的应用了,虽然我考虑到主要是打算介绍,不使用前缀和也是可以通过的。
#include