

在高考数学里,空间直线与平面的平行有关的知识内容和题型,一直是近几年高考命题的热点,成为立体几何重要的基础考点。如何巧妙快速的判定空间直线与平面平行位置关系,如何在平面内寻找一条直线,探索该直线与平面平行等,这些问题一直是常见的热点问题。 重点考查考生的空间想象能力、计算能力、推理论证能力,以及转化思想的应用。 跟着包Sir一起来看看动态教辅里是如何来帮助大家学习这一部分知识的吧~ 小编乱入 1 互动启思

 题型1 直线的倾斜角与斜率、直线方程 引言 掌握基础知识,养成画图的习惯,培养平面几何的想象能力是解题的关键. 例题1
题型1 直线的倾斜角与斜率、直线方程 引言 掌握基础知识,养成画图的习惯,培养平面几何的想象能力是解题的关键. 例题1 经过点M(1,1)且在两坐标轴上截距相等的直线方程为( )
A.x+y-2=0
B.x+y-1=0
C.x=1或y=1
D.x+y-2=0或x-y=0
互动启思 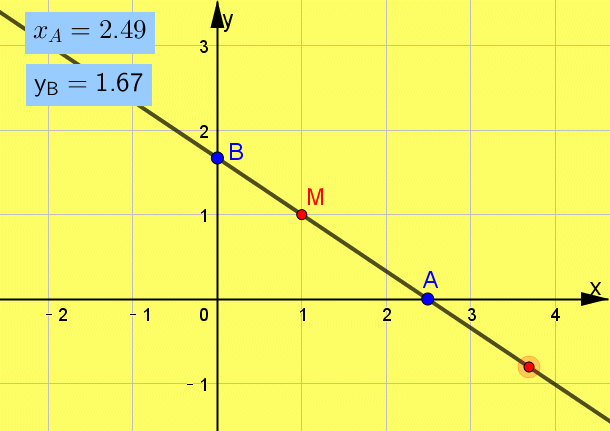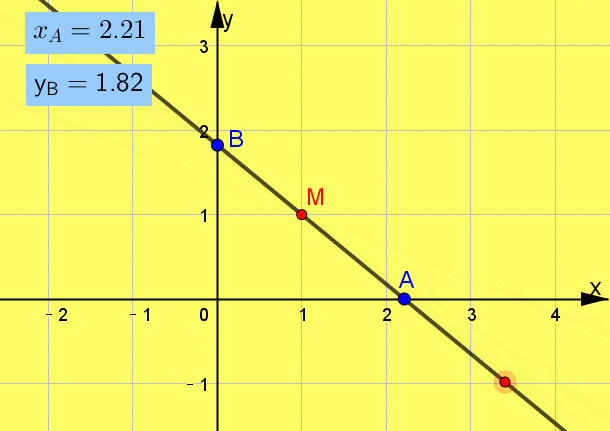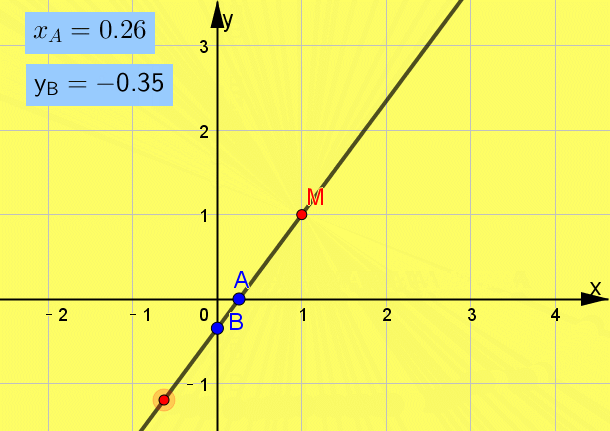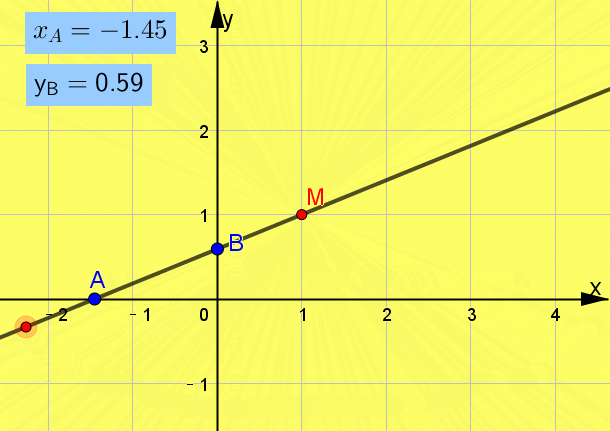 一点呈析 答案:
一点呈析 答案: D
解析: 当直线过原点时,满足题意,此时直线方程为
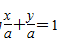
,即
x-
y=0;当直线不过原点时,设直线方程为
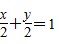
,代入
M(1,1),解得
a=2,所以直线的方程为+=1,即
x+
y-2=0.综上所述,所求直线的方程为
x+
y-2=0或
x-
y=0.故选
例题2 已知直线l平分圆C:x
2+y
2-6x+6y+2=0的周长,且直线l不经过第三象限,则直线l的倾斜角θ的取值范围为( )
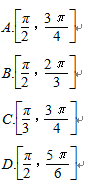 互动启思
互动启思 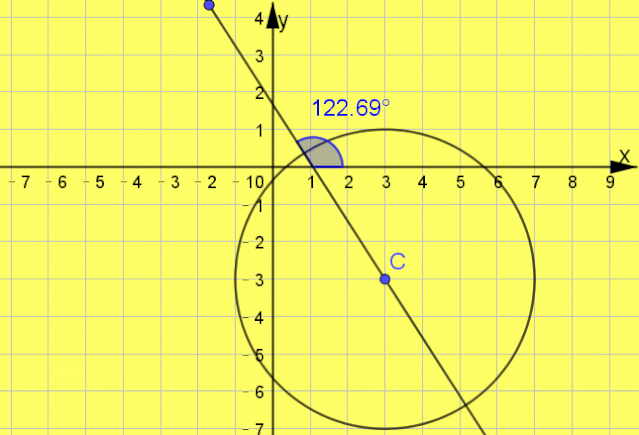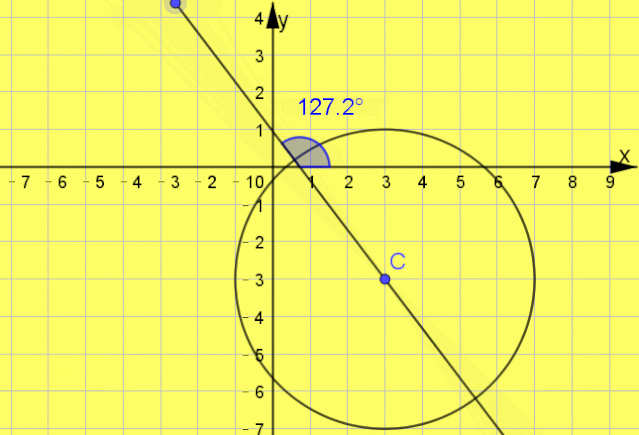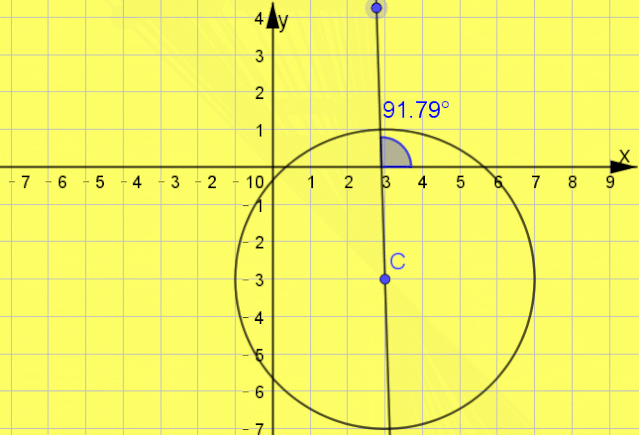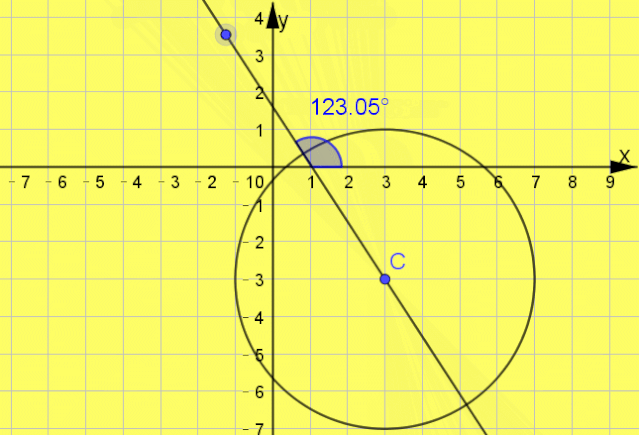 一点呈析 答案:
一点呈析 答案: A
解析: 圆
C:
x2+
y2-6
x+6
y+2=0的标准方程为(
x-3)
2+(
y+3)
2=16,故直线
l过圆
C的圆心(3,-3).因为直线
l不经过第三象限,所以
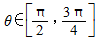
,故选A.

 题型2 两条直线的位置关系 引言 经常会涉及到直线的平行和垂直问题,所以要注意直线平行、垂直的时候,直线的解析式所满足的条件,并且要特别注意不要多解. 例题1
题型2 两条直线的位置关系 引言 经常会涉及到直线的平行和垂直问题,所以要注意直线平行、垂直的时候,直线的解析式所满足的条件,并且要特别注意不要多解. 例题1 “m=-1”是“直线mx+(2m-1)y+1=0和直线3x+my+3=0垂直”的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
互动启思 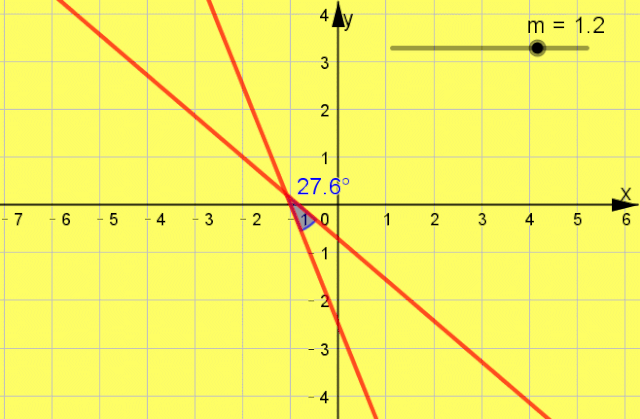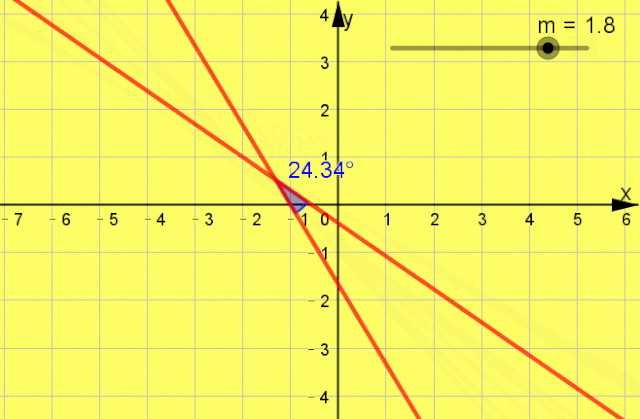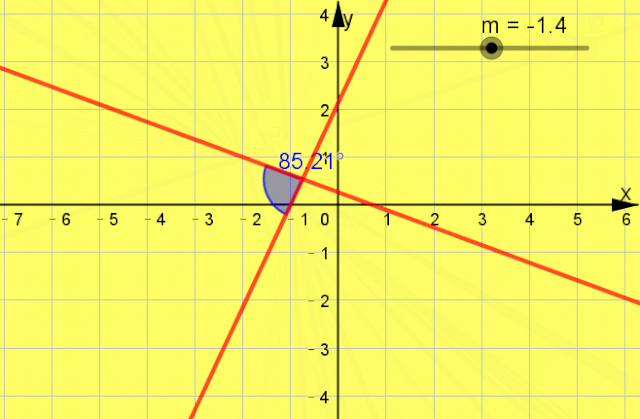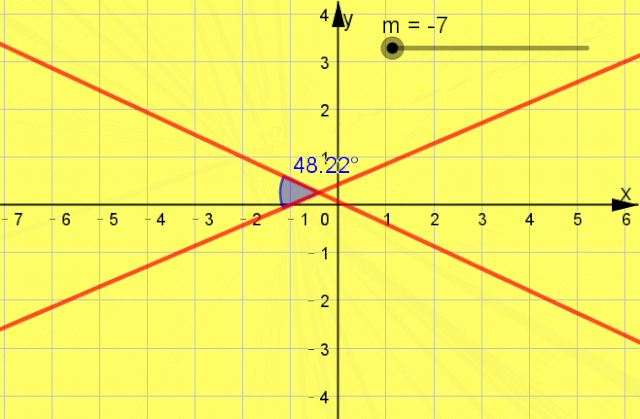 一点呈析 答案:
一点呈析 答案:A
解析:设
p:
m=-1;
q:直线
mx+(2
m-1)
y+1=0和直线3
x+
my+3=0垂直.将
m=-1代入两直线方程,它们的斜率之积为-1,故两直线垂直,从而由
p可以推出
q;但当
m=0时,两直线也垂直,故由
q不一定能推出
p.因而
p是
q的充分不必要条件.故选A.
例题2 已知直线l:
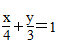
,M是l上一动点,过M作x轴、y轴的垂线,垂足分别为A,B,则在A,B连线上,且满足
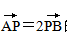
的点P的轨迹方程是 .
互动启思 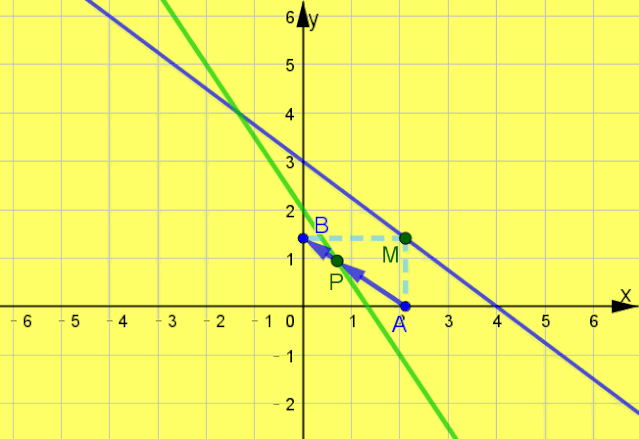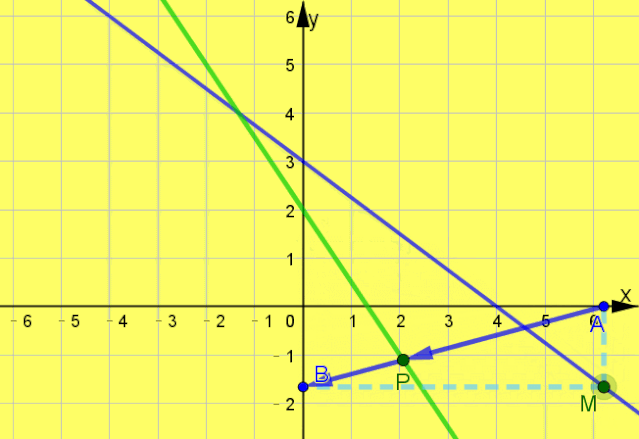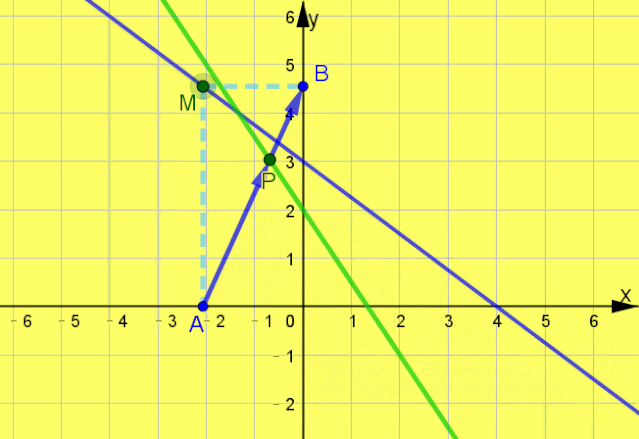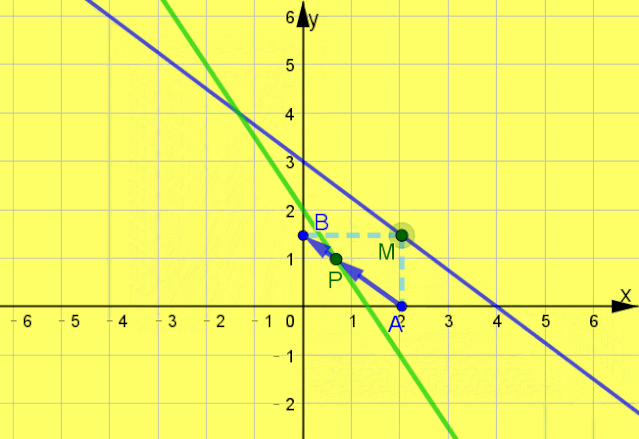 一点呈析 答案:
一点呈析 答案:3x+2y-4=0
解析:设P(x,y)为轨迹上任一点,A(a,0),B(0,b). ∵
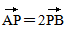
,∴
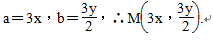
∵点M在直线l上,∴
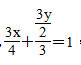
, 整理得3x+2y-4=0, 即3x+2y-4=0为点P的轨迹方程. 2 知识助攻

 1.直线的倾斜角和斜率 (1)直线的倾斜角 ①定义:
1.直线的倾斜角和斜率 (1)直线的倾斜角 ①定义:平面直角坐标系中,对于一条与
x轴相交的直线,把
x轴所在的直线绕着交点按
逆 时针方向旋转到和直线重合时所转的
最小正角 α称为直线的倾斜角.规定:直线与
x轴平行或重合时,直线的倾斜角为
0° ②范围:倾斜角
α的范围是
0°≤α<180°. (2)直线的斜率 ①定义: 当直线的倾斜角
α≠90°时,直线的倾斜角
α的
正切值 叫做这条直线的斜率,常记作
k=
tanα ; 当直线的倾斜角
α=90°时,直线的斜率
不存在 .
②过两点的直线的斜率公式: 过两点
P1(
x1,
y1),
P2(
x2,
y2)(
x1≠
x2)的直线的斜率公式为
k=
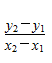
. 若
x1=
x2,则直线
P1P2的倾斜角为90°,斜率不存在。
③范围: 直线的斜率的范围为
R .
敲黑板 (1)不要忽视“直线的斜率不存在”这一情况.在分析直线的倾斜角和斜率的关系时,要根据正切函数k=tanα的单调性,如图所示. 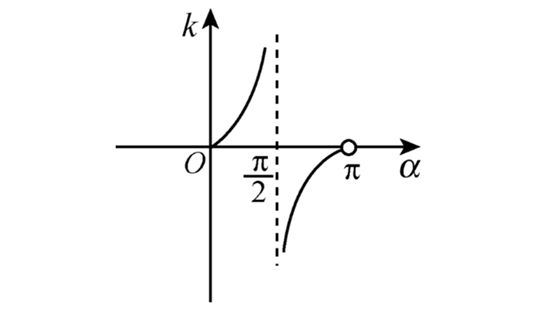 (2)由直线的斜率k求倾斜角α的取值范围时,要对应正切函数的图像来确定,并注意图像的不连续性和函数的定义域.如:由-1≤k≤1,得
(2)由直线的斜率k求倾斜角α的取值范围时,要对应正切函数的图像来确定,并注意图像的不连续性和函数的定义域.如:由-1≤k≤1,得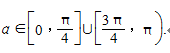 .
. 
 2. 直线的方程 (1) 直线的五种形式
2. 直线的方程 (1) 直线的五种形式 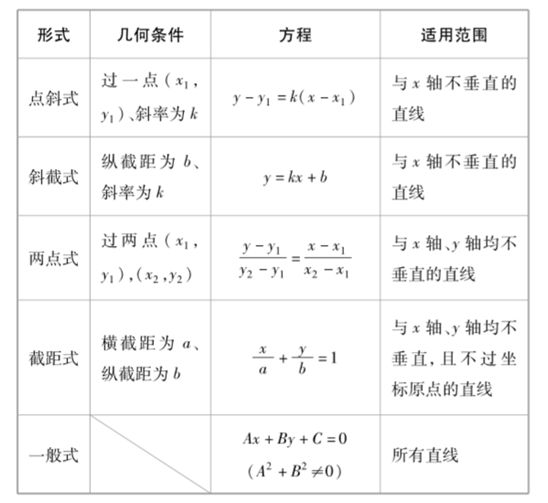 (2) 求直线方程常用的方法
(2) 求直线方程常用的方法 ①根据已知条件,设出适当的直线方程; ②把已知条件构造成含待定系数的方程(组); ③求解待定系数; ④将求得的系数代入设出的直线方程.
敲黑板 若使用斜截式或点斜式设直线方程时,应先讨论斜率k是否存在.同理,在使用截距式前要讨论截距是否存在,是否为0. 
 3.两条直线的位置关系 (1)两条直线的位置关系
3.两条直线的位置关系 (1)两条直线的位置关系 直线
l1:
y=
k1x+
b1与
l2:
y=
k2x+
b2, 直线
l3:
A1x+
B1y+
C1=0与
l4:
A2x+
B2y+
C2=0的位置关系如下表:
 (2)两条直线的交点坐标
(2)两条直线的交点坐标 当两条直线相交时,
两直线的方程联立的方程组的解即为交点坐标. (3)距离公式 ①两点间的距离: 平面上两点P
1(x
1,y
1),P
2(x
2,y
2)之间的距离公式为|P
1P
2|=
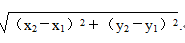 ②点到直线的距离:
②点到直线的距离: 平面上的点P(x
0,y
0)到直线l:Ax+By+C=0的距离公式为d=
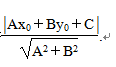 ③两条平行直线间的距离:
③两条平行直线间的距离: 直线l
1:Ax+By+C
1=0与l
2:Ax+By+C
2=0之间的距离公式为d=
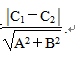

 4.两条直线平行与垂直的判定及应用 (1)两条直线平行或垂直的判定方法 <1>已知两直线的斜率一定存在
4.两条直线平行与垂直的判定及应用 (1)两条直线平行或垂直的判定方法 <1>已知两直线的斜率一定存在 ①两直线平行⇔两直线的斜率相等且在相应坐标轴上的截距不相等; ②两直线垂直⇔两直线的斜率之积为-1.
<2>两直线的斜率可能不存在 若两直线斜率不存在,当两直线在
x轴上的截距不相等时,两直线平行;否则,两直线重合. 若两直线中有一条直线的斜率不存在,另一条直线的斜率为0,则两直线互相垂直.
<3>已知两直线的一般方程 直接应用有关结论判定;也可利用直线方程求出斜率(或判定出斜率不存在),转化为<1><2>中的情形进行判定.
(2)两条直线平行与垂直的应用
当直线方程中的系数含有参数时,参数的不同取值决定了直线的不同位置,因此应对参数的取值进行分类讨论,一般分为斜率存在和斜率不存在两种情况,再根据不同情况下应满足的关系,列式求解.或直接应用“知识划重点”中l
3,l
4所满足的条件列式求解.
敲黑板 根据位置关系转化为等量关系(不等关系)时,要注意等价性.如两直线平行⇔k1=k2且b1≠b2(或A1B2-A2B1=0且A1C2-A2C1≠0),此时不要只得出k1=k2(或A1B2-A2B1=0).另外,求出参数值时注意代回检验,避免产生增根.
解答这类题通常有两种方法: ①根据l
1∥l
2⇒k
1=k
2,l
1⊥l
2⇒k
1·k
2=-1确定待求直线的斜率,再由点斜式得到直线的方程. ②由两直线平行(垂直)的方程特征设出方程,再由待定系数法求解.

 5.两条直线的交点与距离 (1)求两直线的交点坐标
5.两条直线的交点与距离 (1)求两直线的交点坐标 设两条直线的方程为l
1:A
1x+B
1y+C
1=0,l
2:A
2x+B
2y+C
2=0,则方程组
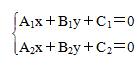
的解就是两条直线的交点坐标. ①若方程组有唯一解,则两条直线
相交 ,此解就是交点的坐标; ②若方程组无解,则两条直线
无公共点 ,此时两条直线
平行 ,反之亦成立.
(2)距离公式的应用
应用距离公式求解即可. 敲黑板 ①求点到直线的距离时,必须把直线方程化为一般式Ax+By+C=0. ②求两条平行直线间的距离时,一定要把直线方程中x,y的系数化成一致的.
借助距离公式首先建立方程(组)得出参数的值或满足的关系式,然后结合题中其他条件确定方程、点的坐标等.
敲黑板 若已知点到直线的距离求直线方程,用一般式可避免讨论.否则,应讨论斜率是否存在. 
 6.对称问题 (1) 点关于点对称
6.对称问题 (1) 点关于点对称 若点A(x
1,y
1)和点B(x
2,y
2)关于点C(a,b)对称,则由中点坐标公式得
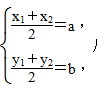
从而可解.
(2)直线关于点对称 方法1:根据两对称直线平行,求出已知直线上任一点的对称点,由点斜式可求对称直线的方程;
方法2:在已知直线上任取两点,分别求出两个对称点,由两点式可求得对称直线的方程.
(3)点关于直线对称 若点A(x
1,y
1)和点B(x
2,y
2)关于直线l:Ax+By+C=0对称,则满足方程组
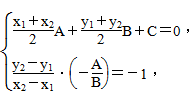
进而求解
(4)直线关于直线对称 (1)若l
1∥l
2,l
1与l
2关于直线l对称,则可利用平行线间距离公式求解; (2)若l
1∩l
2=A,l
1与l
2关于直线l对称,且点A在直线l上,求出直线l
1上任一点关于直线l的对称点B,由
两点式 可求得对称直线的方程.
敲黑板 点关于点的对称是基本问题,也是各种对称问题可转化的最终问题.抓住两点:一是“垂直”,两对称点连线与对称轴垂直;二是“平分”,两对称点连线段的中点在对称轴上. 声明:以上内容摘自包学习APP_动态教辅《 数学丨动态题型包 》,欢迎来包学习和更多小伙伴一起学习更多知识吧。

点击

 在高考数学里,空间直线与平面的平行有关的知识内容和题型,一直是近几年高考命题的热点,成为立体几何重要的基础考点。如何巧妙快速的判定空间直线与平面平行位置关系,如何在平面内寻找一条直线,探索该直线与平面平行等,这些问题一直是常见的热点问题。 重点考查考生的空间想象能力、计算能力、推理论证能力,以及转化思想的应用。 跟着包Sir一起来看看动态教辅里是如何来帮助大家学习这一部分知识的吧~ 小编乱入 1 互动启思
在高考数学里,空间直线与平面的平行有关的知识内容和题型,一直是近几年高考命题的热点,成为立体几何重要的基础考点。如何巧妙快速的判定空间直线与平面平行位置关系,如何在平面内寻找一条直线,探索该直线与平面平行等,这些问题一直是常见的热点问题。 重点考查考生的空间想象能力、计算能力、推理论证能力,以及转化思想的应用。 跟着包Sir一起来看看动态教辅里是如何来帮助大家学习这一部分知识的吧~ 小编乱入 1 互动启思  一点呈析 答案: D 解析: 当直线过原点时,满足题意,此时直线方程为
一点呈析 答案: D 解析: 当直线过原点时,满足题意,此时直线方程为 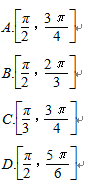 互动启思
互动启思  一点呈析 答案: A 解析: 圆C:x2+y2-6x+6y+2=0的标准方程为(x-3)2+(y+3)2=16,故直线l过圆C的圆心(3,-3).因为直线l不经过第三象限,所以
一点呈析 答案: A 解析: 圆C:x2+y2-6x+6y+2=0的标准方程为(x-3)2+(y+3)2=16,故直线l过圆C的圆心(3,-3).因为直线l不经过第三象限,所以  一点呈析 答案:A 解析:设p:m=-1;q:直线mx+(2m-1)y+1=0和直线3x+my+3=0垂直.将m=-1代入两直线方程,它们的斜率之积为-1,故两直线垂直,从而由p可以推出q;但当m=0时,两直线也垂直,故由q不一定能推出p.因而p是q的充分不必要条件.故选A. 例题2 已知直线l:
一点呈析 答案:A 解析:设p:m=-1;q:直线mx+(2m-1)y+1=0和直线3x+my+3=0垂直.将m=-1代入两直线方程,它们的斜率之积为-1,故两直线垂直,从而由p可以推出q;但当m=0时,两直线也垂直,故由q不一定能推出p.因而p是q的充分不必要条件.故选A. 例题2 已知直线l:  一点呈析 答案:3x+2y-4=0 解析:设P(x,y)为轨迹上任一点,A(a,0),B(0,b). ∵
一点呈析 答案:3x+2y-4=0 解析:设P(x,y)为轨迹上任一点,A(a,0),B(0,b). ∵
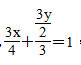 , 整理得3x+2y-4=0, 即3x+2y-4=0为点P的轨迹方程. 2 知识助攻
, 整理得3x+2y-4=0, 即3x+2y-4=0为点P的轨迹方程. 2 知识助攻 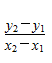 . 若x1=x2,则直线P1P2的倾斜角为90°,斜率不存在。 ③范围: 直线的斜率的范围为 R . 敲黑板 (1)不要忽视“直线的斜率不存在”这一情况.在分析直线的倾斜角和斜率的关系时,要根据正切函数k=tanα的单调性,如图所示.
. 若x1=x2,则直线P1P2的倾斜角为90°,斜率不存在。 ③范围: 直线的斜率的范围为 R . 敲黑板 (1)不要忽视“直线的斜率不存在”这一情况.在分析直线的倾斜角和斜率的关系时,要根据正切函数k=tanα的单调性,如图所示.  (2)由直线的斜率k求倾斜角α的取值范围时,要对应正切函数的图像来确定,并注意图像的不连续性和函数的定义域.如:由-1≤k≤1,得
(2)由直线的斜率k求倾斜角α的取值范围时,要对应正切函数的图像来确定,并注意图像的不连续性和函数的定义域.如:由-1≤k≤1,得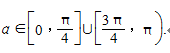 .
.  (2) 求直线方程常用的方法 ①根据已知条件,设出适当的直线方程; ②把已知条件构造成含待定系数的方程(组); ③求解待定系数; ④将求得的系数代入设出的直线方程. 敲黑板 若使用斜截式或点斜式设直线方程时,应先讨论斜率k是否存在.同理,在使用截距式前要讨论截距是否存在,是否为0.
(2) 求直线方程常用的方法 ①根据已知条件,设出适当的直线方程; ②把已知条件构造成含待定系数的方程(组); ③求解待定系数; ④将求得的系数代入设出的直线方程. 敲黑板 若使用斜截式或点斜式设直线方程时,应先讨论斜率k是否存在.同理,在使用截距式前要讨论截距是否存在,是否为0.  (2)两条直线的交点坐标 当两条直线相交时,两直线的方程联立的方程组的解即为交点坐标. (3)距离公式 ①两点间的距离: 平面上两点P1(x1,y1),P2(x2,y2)之间的距离公式为|P1P2|=
(2)两条直线的交点坐标 当两条直线相交时,两直线的方程联立的方程组的解即为交点坐标. (3)距离公式 ①两点间的距离: 平面上两点P1(x1,y1),P2(x2,y2)之间的距离公式为|P1P2|= 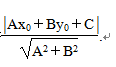 ③两条平行直线间的距离: 直线l1:Ax+By+C1=0与l2:Ax+By+C2=0之间的距离公式为d=
③两条平行直线间的距离: 直线l1:Ax+By+C1=0与l2:Ax+By+C2=0之间的距离公式为d= 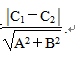
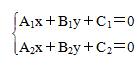 的解就是两条直线的交点坐标. ①若方程组有唯一解,则两条直线 相交 ,此解就是交点的坐标; ②若方程组无解,则两条直线 无公共点 ,此时两条直线 平行 ,反之亦成立. (2)距离公式的应用
的解就是两条直线的交点坐标. ①若方程组有唯一解,则两条直线 相交 ,此解就是交点的坐标; ②若方程组无解,则两条直线 无公共点 ,此时两条直线 平行 ,反之亦成立. (2)距离公式的应用
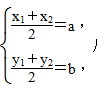 从而可解. (2)直线关于点对称 方法1:根据两对称直线平行,求出已知直线上任一点的对称点,由点斜式可求对称直线的方程; 方法2:在已知直线上任取两点,分别求出两个对称点,由两点式可求得对称直线的方程. (3)点关于直线对称 若点A(x1,y1)和点B(x2,y2)关于直线l:Ax+By+C=0对称,则满足方程组
从而可解. (2)直线关于点对称 方法1:根据两对称直线平行,求出已知直线上任一点的对称点,由点斜式可求对称直线的方程; 方法2:在已知直线上任取两点,分别求出两个对称点,由两点式可求得对称直线的方程. (3)点关于直线对称 若点A(x1,y1)和点B(x2,y2)关于直线l:Ax+By+C=0对称,则满足方程组 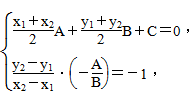 进而求解 (4)直线关于直线对称 (1)若l1∥l2,l1与l2关于直线l对称,则可利用平行线间距离公式求解; (2)若l1∩l2=A,l1与l2关于直线l对称,且点A在直线l上,求出直线l1上任一点关于直线l的对称点B,由 两点式 可求得对称直线的方程. 敲黑板 点关于点的对称是基本问题,也是各种对称问题可转化的最终问题.抓住两点:一是“垂直”,两对称点连线与对称轴垂直;二是“平分”,两对称点连线段的中点在对称轴上. 声明:以上内容摘自包学习APP_动态教辅《 数学丨动态题型包 》,欢迎来包学习和更多小伙伴一起学习更多知识吧。
进而求解 (4)直线关于直线对称 (1)若l1∥l2,l1与l2关于直线l对称,则可利用平行线间距离公式求解; (2)若l1∩l2=A,l1与l2关于直线l对称,且点A在直线l上,求出直线l1上任一点关于直线l的对称点B,由 两点式 可求得对称直线的方程. 敲黑板 点关于点的对称是基本问题,也是各种对称问题可转化的最终问题.抓住两点:一是“垂直”,两对称点连线与对称轴垂直;二是“平分”,两对称点连线段的中点在对称轴上. 声明:以上内容摘自包学习APP_动态教辅《 数学丨动态题型包 》,欢迎来包学习和更多小伙伴一起学习更多知识吧。  点击
点击