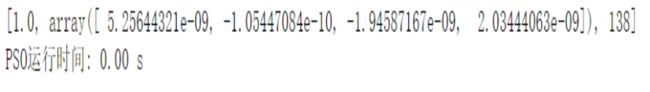粒子群优化算法python实现

一、粒子群优化算法是什么？

粒子群优化算法(Particle Swarm Optimization, PSO)作为进化计算的一个分支，是由Eberhart和Kennedy于1995年提出的一种全局搜索算法，同时它也是一种模拟自然界的生物活动以及群体智能的随即搜索算法。

粒子群优化算法起源于鸟群觅食的过程，一个核心机制是每只小鸟各自觅食，并记住一个离食物最近的位置，通过和其他的小鸟交流，得到整个鸟群已知的最佳位置，引导鸟群朝着这个方向继续搜索。

还有两个关键设置：粒子历史最优位置(pBest向量)、群体历史最优位置(gBest向量)。

这里pBest向量是一组向量，它包含了每个粒子的历史最优位置，gBest向量为pBest向量中适应值最高的向量，即全局最优。

说明：算法中一般取要优化的目标函数作为适应值函数，评估适应值的大小，然后更新pBest向量和gBest向量。

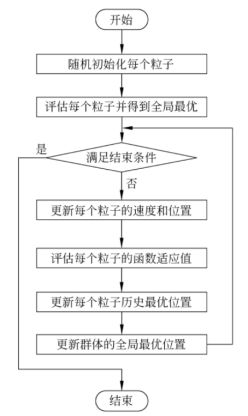
二、算法流程

（1）初始化所有个体（粒子），初始化它们的速度和位置，并且将个体的历史最优位置pBest设为当前位置，而群体中最优的个体作为当前的gBest。

（2）在每一代的进化中，计算各个粒子的适应度函数值。

（3）如果该粒子当前的适应度函数值比其历史最优值要好，那么历史最优将会被当前位置所代替。

（4）如果该粒子的历史最优比全局最优要好，那么全局最优将会被该粒子的历史最优所替代。

（5）对每个粒子i的第d维的速度和位置分别按照下列公式进行更新。这两个公式在二维空间中的关系如下图。

ω是惯量权重，一般初始化为0.9，随着迭代过程线性递减到0.4 ; c1和c2是加速系数(也称学习因子)，传统上取固定值2.0 ; rand1d是和rand2d是两个[0,1]之间的随机数。另外，设置一个Vmax限制速度的范围，Vmax的每一维Vmaxd一般取相应维的取值范围的10%~20%。更新后检查位置是否在问题空间内。这里ω做一个线性递减是因为，在算法一开始，群体没有一个方向做指导，所以需要一个任意性，进行搜索；而随着算法的迭代，群体已经有了一个指导方向，就不再需要很大的任意性，而是受个体历史最优和群体历史最优的影响越来越大。

（6）如果还没有到达结束条件，转到（2），否则输出gBest并结束。

下图为算法的流程图。

三、算法的python实现

本算法以优化目标函数：

为例，使用粒子群优化算法进行求解。

运行环境：python3.6，jupyter notebook

# 目标函数值计算
def f(C):
    return 1/(C[0]**2+C[1]**2+C[2]**2+C[3]**2+1)
# 初始化种群 C=[[[x],[v]]]
def init(N):
    C = np.zeros((N,2,4))
    global pBest,gBest
    for i in range(N):
        for j in range(4):
            C[i][0][j] = np.random.uniform(-5,5)
            C[i][1][j] = np.random.uniform(-1,1)
        pBest[i] = C[i][0]
    gBest = pBest[np.argmax(Eval(C,N))].copy()
    return C
# 判断更新后是否还在问题空间内
def whether_out(C):
    for i in range(len(C)):
        for j in range(4):
            if C[i][0][j] < -5 :
                C[i][0][j] = -5
            elif C[i][0][j] > 5:
                C[i][0][j] = 5
    return C

# 更新粒子的速度和位置
def update_C(C,N,w,c1,c2):
    '''
    C:种群 [[[x],[v]]]
    N:种群规模 100
    w:惯量权重 初始0.9，递减到0.4
    c1、c2:加速系数
    pBest: 每个粒子的历史最优位置[[x]]
    gBest: 全局最优位置[x]
    '''
#     print(C.shape)
    for i in range(N):
        for j in range(4):
            rand1 = np.random.random()
            rand2 = np.random.random()
            C[i][1][j] = w*C[i][1][j]+c1*rand1*(pBest[i][j]-C[i][0][j])+c2*rand2*(gBest[j]-C[i][0][j])
            C[i][0][j] +=  C[i][1][j]
    C = whether_out(C)
    return C
        
# 评估函数
def Eval(C,N):
    temp = np.array([])
    for i in range(N):
        temp = np.append(temp,f(C[i][0]))
    return temp
# 更新粒子的历史最优和全局最优
def update_best(C,N,fitness):
    '''
    pBest: 每个粒子的历史最优位置,[[x]]
    gBest: 全局最优位置,[x]
    fitness: 粒子当前适应值,[f(x)]
    '''
    global pBest,gBest
    for i in range(N):
        if fitness[i] > f(pBest[i]):
            pBest[i] = C[i][0]
        if fitness[i] > f(gBest):
            gBest = C[i][0].copy()
# w线性递减
def w_degression(w,N):
    w -= 0.5/N
    return w

def PSO(length,N,w,c1,c2):
    global pBest,gBest
    C = init(N)
#     print('gBest:',gBest)
    for i in range(length):
        C = update_C(C,N,w,c1,c2)
        fitness = Eval(C,N)
        update_best(C,N,fitness)
        w=w_degression(w,N)
        if f(gBest)==1.0:
            break
    return [f(gBest),gBest,i]

start = time.time()
c1,c2 = 2,2
# length:迭代次数，N:种群规模
length,N=1000,30
w=0.9
pBest = np.zeros((N,4))
gBest = np.zeros(N)
# PSO(length,N,w,c1,c2)
end = time.time()
print(PSO(length,N,w,c1,c2))
print('PSO运行时间: %.2f s'%(end-start))

实验结果

当种群数设置为100时

当种群数设置为30时