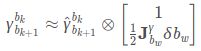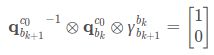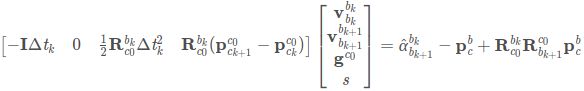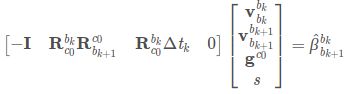VINS-Mono学习（二）——松耦合初始化

初始化：如何当好一个红娘？

图解SfM

视觉和IMU的羁绊

怎么知道发生了闭环？

位姿图优化与滑窗优化都为哪般？

闭环优化：拉扯橡皮条

整体初始化流程如下：

        1、SFM纯视觉估计滑动窗口内所有帧的位姿和3D路标点的逆深度；

        2、SFM与IMU预积分松耦合，对齐求解初始化参数。

        下面主要按这两个步骤进行讲解。

1、SfM纯视觉运动估计

       

1.1 视觉几何相关基础

        1、已知两帧图像：特征点提取fast，匹配（光流，特征描述子）；

        2、已知两帧图像特征匹配点：利用对极集合约束（E矩阵，H矩阵），计算两图像之间的pose（update to scale）；

        3、已知相机pose，已知特征点二维坐标：通过三角化得到三维坐标；

        4、已知3d点，3d特征点：通过Perspective-n-Point(PnP)求取新的相机pose。

 

        初始化代码在estimator.cpp文件的processImage()函数中，具体在第三个步骤中完成VIO的初始化，代码如下：

// Step 3： VIO初始化
if( ESTIMATE_EXTRINSIC != 2 && (header.stamp.toSec() - initial_timestamp) > 0.1)
{
   result = initialStructure();
   initial_timestamp = header.stamp.toSec();
}

        具体来看initialStructure()函数的大致代码与流程如下：

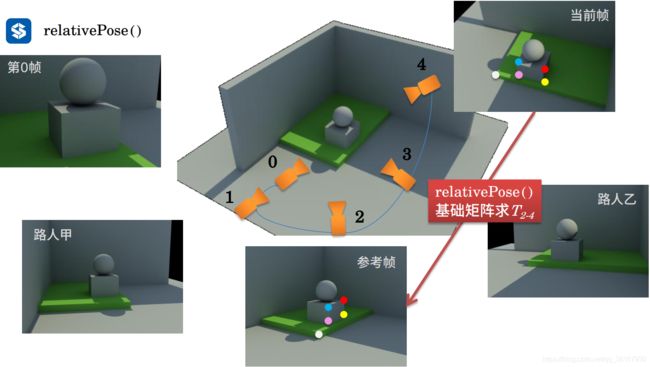
        为了解释视觉初始化，给定一个场景进行解释：

2.1 初始化代码：视觉部分

        initialStructure()函数中首先进行的是视觉部分的初始化操作：

可以看到主要用了三个函数：

        1. relativePose：计算当前帧跟参考帧的相对位姿

        2. GlobalSFM::construct：SfM计算滑窗内的路标点和相机位姿

        3. cv::solvePnP：计算所有位姿

        4. visualInitialAlign：视觉和IMU对齐，这个函数在讲完IMU预积分之后再讲，具体见《2.2.2节》。

        这里说回initialStructure()函数，initial的过程如下：

        Step1：检测IMU可观性；

                1.1 求加速度累计和 及 平均值；

                1.2 根据上面的平均值求加速度方差

                1.3 根据方差求加速度标准差。

        Step2：纯视觉SFM

                2.1 遍历所有特征点，每个特征点构造一个sfmFeature

                2.2 求解当前帧（滑窗内最后一帧）与滑窗内最近的参考帧的相对位姿。（relativePose(R,T,l)函数） 

                2.3 构造sfm问题，进行sfm求解。（sfm.construct()函数）

        （PS：这个construct()函数比较重要，一是因为滑窗内关键帧的初始化顺序；二是solveFrameByPnP()函数利用特征点在世界坐标系下的表示和在当前帧下的投影，计算出当前帧位姿R_cw；三是注意这里还有三角化处理，用的是当前帧 和 最后一帧或者参考帧）。

                2.4 对所有帧求解PnP，利用关键帧对all_image_frame中的非关键帧进行初始化。（cv::solvePnP()函数。）

         Step3：视觉惯性对齐。（visualInitialAlign()函数）

        下面按上面步骤对这个initialStructure()函数进行展开详细讲解。

2.1.1 遍历所有特征点，构造一个sfmFeature

2.1.2 relativePose() 求解当前帧跟参考帧的位姿

        1. 找参考帧：寻找与当前帧的共视点数较多、且视差量较大的作为参考帧；

        2. 有足够的视差，再通过2D-2D对极约束，求基础矩阵，计算出当前帧到参考帧的相对位姿T。

         举个例子说明上述寻找参考帧以及建立共视点关系的情况：

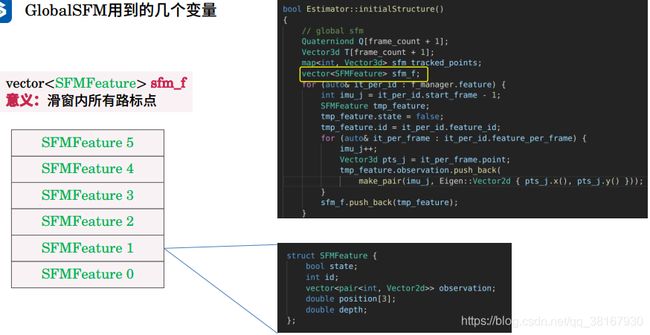
2.1.3 GlobalSFM::construct() 流程

        在讲解construct()函数前，首先看一下GlobalSFM中用到的几个变量：

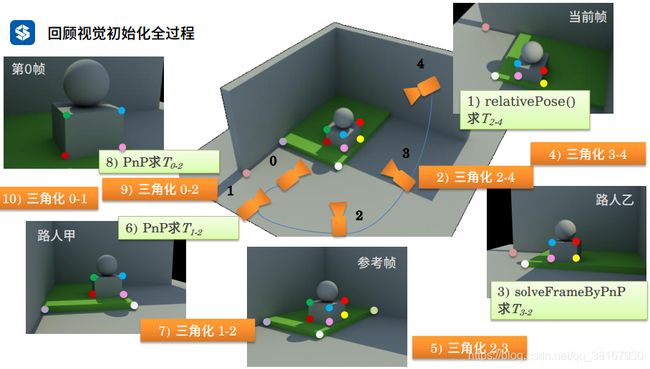
construct()函数的代码流程如下：

再对上述步骤进行拆解：

补充三角化其他未恢复的点：

最后进行一次全局BA：

Ceres自动求导过程如下：

 

 

2.1.4 计算所有帧位姿 

 

 

---

2、SFM与IMU预积分松耦合

        视觉惯性对齐函数visualInitialAlign()函数主要调用了VisualIMUAlignment()函数，这两个函数优点像。

        visualInitialAlign()处理的事情比较多一些，除了对齐视觉和IMU之外，还要

2.1 IMU预积分技术基础

2.1.1 IMU传感器模型

        测量值为真实值+噪声+bias偏置。

补充知识：加速度计和陀螺仪的误差可以分为：确定性误差，随机误差。

• 确定性误差可以事先标定，包括：bias，scale...
• 随机误差通常假设噪声服从高斯分布，包括：高斯白噪声，bias随机游走... 

2.2.2 IMU预积分

        将一段时间内的IMU数据直接积分起来就能得到i，j之间关于IMU的测量约束，即预积分量：

重新整理下PVQ的积分公式，有：

 

预积分的离散形式：

        采用mid-point方法，即两个相邻时刻k到k+1的位姿是用两个时刻的测量值a，w的平均值来计算：

 

 

2.2 视觉SFM和IMU预积分对齐 

2.2.1 视觉和IMU之间的联系 

        视觉SFM和IMU预积分之间存在的几何约束如下：考虑相机坐标系c0为世界坐标系，则利用外参数qbc，tbc构建等式：

其中，s为尺度因子，表示非米制单位的轨迹。等式（3）等价于：

 

2.2.2 视觉和IMU对齐流程 

        下面这个几个步骤是视觉sfm和IMU预积分对齐的

1、若没有外参，先估计旋转外参数 

图中的公式（5）关系来源于下图：

继续对式（6）进行如下操作：

        上面的函数在estimator.cpp文件中的Estimator::processImage()函数中调用，在Step2中就会进行外参初始化调用initial_ex_rotation.CalibrationExRotation()函数进行外参估计，得到外参数calib_ric，代码如下：

// 标定imu和相机之间的旋转外参，通过imu和图像计算的旋转使用手眼标定计算获得
bool InitialEXRotation::CalibrationExRotation(vector> corres, Quaterniond delta_q_imu, Matrix3d &calib_ric_result)
{
    frame_count ++;
    // 根据特征关联求解两个连续帧相机的旋转R12
    Rc.push_back(solveRelativeR(corres));
    Rimu.push_back(delta_q_imu.toRotationMatrix());
    // 通过外参把imu的旋转转移到相机坐标系
    Rc_g.push_back(ric.inverse() * delta_q_imu * ric);  // ric是上一次求解得到的外参

    Eigen::MatrixXd A(frame_count * 4, 4);
    A.setZero();
    int sum_ok = 0;
    for (int i = 1; i <= frame_count; i++)
    {
        Quaterniond r1(Rc[i]);
        Quaterniond r2(Rc_g[i]);

        // 角度误差r_k+1^k，用于后面的鲁棒核权重求解
        double angular_distance = 180 / M_PI * r1.angularDistance(r2);
        ROS_DEBUG("%d %f", i, angular_distance);
        // 一个简单的核函数，式（8）中w的求解
        double huber = angular_distance > 5.0 ? 5.0 / angular_distance : 1.0;
        ++ sum_ok;
        Matrix4d L, R;

        double w = Quaterniond(Rc[i]).w();
        Vector3d q = Quaterniond(Rc[i]).vec();
        L.block<3, 3>(0, 0) = w * Matrix3d::Identity() + Utility::skewSymmetric(q);
        L.block<3, 1>(0, 3) = q;
        L.block<1, 3>(3, 0) = -q.transpose();
        L(3, 3) = w;

        Quaterniond R_ij(Rimu[i]);
        w = R_ij.w();
        q = R_ij.vec();
        R.block<3, 3>(0, 0) = w * Matrix3d::Identity() - Utility::skewSymmetric(q);
        R.block<3, 1>(0, 3) = q;
        R.block<1, 3>(3, 0) = -q.transpose();
        R(3, 3) = w;

        // 公式（7）
        A.block<4, 4>((i - 1) * 4, 0) = huber * (L - R);    // 作用在残差上面
    }

    // 对公式（7）采用SVD分解
    JacobiSVD svd(A, ComputeFullU | ComputeFullV);
    Matrix x = svd.matrixV().col(3);
    Quaterniond estimated_R(x);     // 用上面的Matrix初始化四元数
    ric = estimated_R.toRotationMatrix().inverse();
    // cout << svd.singularValues().transpose() << endl;
    // cout << ric << endl;
    Vector3d ric_cov;
    ric_cov = svd.singularValues().tail<3>();
    // 倒数第二个奇异值，因为旋转是3个自由度，因此检查一下第三小的奇异值是否足够大，通常需要足够的运动激励才能保证得到没有奇异的解
    if (frame_count >= WINDOW_SIZE && ric_cov(1) > 0.25)
    {
        calib_ric_result = ric;
        return true;
    }
    else
        return false;
}

补充知识：为什么要取第4个向量作为结果？

2、利用旋转约束估计陀螺仪bias 

        剩下的这三个函数实际都在visualInitialAlign()函数中，

        课件里写得比较简洁，很多过程都省略了，看代码的时候就云里雾里看不明白，这里参照https://blog.csdn.net/jiweinanyi/article/details/99882311，给定完整的陀螺仪bias校正过程：

        对于窗口中的连续两帧和，已经从视觉SFM中得到了旋转和 ，从预积分中得到了相邻两帧旋转，根据约束方程，建立所有相邻帧最小代价函数：

其中，对陀螺仪偏置求IMU预积分项线性化，有：

在具体实现的时候，上述约束方程为：

有：

代入上一阶展开式，有：

只考虑虚部，有： 

两侧乘以，用LDLT分解求得δbw​。

然后用LDLT分解求得偏置δbw​。代码如下：

void solveGyroscopeBias(map &all_image_frame, Vector3d* Bgs)
{
    Matrix3d A;
    Vector3d b;
    Vector3d delta_bg;

    A.setZero();
    b.setZero();
    map::iterator frame_i;
    map::iterator frame_j;
    for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++)
    {
        frame_j = next(frame_i);      // 找到下一帧
        MatrixXd tmp_A(3, 3);   // H = J^T*J
        tmp_A.setZero();
        VectorXd tmp_b(3);         // r
        tmp_b.setZero();
        
        //R_ij = (R^c0_bk)^-1 * (R^c0_bk+1) 转换为四元數 q_ij = (q^c0_bk)^-1 * (q^c0_bk+1)
        Eigen::Quaterniond q_ij(frame_i->second.R.transpose() * frame_j->second.R);
        //tmp_A = J_j_bw
        tmp_A = frame_j->second.pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
        //tmp_b = 2 * ((r^bk_bk+1)^-1 * (q^c0_bk)^-1 * (q^c0_bk+1))_vec
        //      = 2 * ((r^bk_bk+1)^-1 * q_ij)_vec
        tmp_b = 2 * (frame_j->second.pre_integration->delta_q.inverse() * q_ij).vec();
        //tmp_A * delta_bg = tmp_b
        A += tmp_A.transpose() * tmp_A;
        b += tmp_A.transpose() * tmp_b;
    }

    delta_bg = A.ldlt().solve(b);   // 求出陀螺仪bias的差值
    ROS_WARN_STREAM("gyroscope bias initial calibration " << delta_bg.transpose());
    // 滑窗中的零偏设置为求解出来的零偏
    for (int i = 0; i <= WINDOW_SIZE; i ++)
        Bgs[i] += delta_bg;

    // 对all_image_frame中预积分量根据当前零偏重新积分
    for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end( ); frame_i++)
    {
        frame_j = next(frame_i);
        frame_j->second.pre_integration->repropagate(Vector3d::Zero(), Bgs[0]);
    }
}

3、利用平移约束估计重力，速度，以及尺度因子s 

 

 

 

根据待优化变量，整理上述方程，转换成Hx=b的形式，有：

转换成矩阵形式：

同理有：

最后得到： 

 也就是：

接下来看LinearAlignment()函数：

bool LinearAlignment(map &all_image_frame, Vector3d &g, VectorXd& x)
{
    // 这一部分内容对照论文进行理解
    // 这里是《VIO 第7讲》 —— 视觉与IMU对齐估计流程第3步：利用平移约束估计重力、速度以及尺度初始值
    int all_frame_count = all_image_frame.size();
    int n_state = all_frame_count * 3 + 3 + 1;      // 速度 + 重力 + 尺度因子

    MatrixXd A{n_state, n_state};
    A.setZero();
    VectorXd b{n_state};
    b.setZero();

    map::iterator frame_i;
    map::iterator frame_j;
    int i = 0;
    for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i ++, i ++)
    {
        frame_j = next(frame_i);

        MatrixXd tmp_A(6, 10);
        tmp_A.setZero();
        VectorXd tmp_b(6);
        tmp_b.setZero();

        double dt = frame_j->second.pre_integration->sum_dt;
        // 《VIO第7讲》，公式（17）
        tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
        tmp_A.block<3, 3>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity();
        tmp_A.block<3, 1>(0, 9) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;     
        tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0];
        // cout << "delta_p   " << frame_j->second.pre_integration->delta_p.transpose() << endl;
        tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
        tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
        tmp_A.block<3, 3>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity();
        tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v;
        // cout << "delta_v   " << frame_j->second.pre_integration->delta_v.transpose() << endl;

        Matrix cov_inv = Matrix::Zero();
        // cov.block<6, 6>(0, 0) = IMU_cov[i + 1];
        // MatrixXd cov_inv = cov.inverse();
        cov_inv.setIdentity();

        MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
        VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;

        A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
        b.segment<6>(i * 3) += r_b.head<6>();

        A.bottomRightCorner<4, 4>() += r_A.bottomRightCorner<4, 4>();
        b.tail<4>() += r_b.tail<4>();

        A.block<6, 4>(i * 3, n_state - 4) += r_A.topRightCorner<6, 4>();
        A.block<4, 6>(n_state - 4, i * 3) += r_A.bottomLeftCorner<4, 6>();
    }

    // 增强数值稳定性
    A = A * 1000.0;
    b = b * 1000.0;
    x = A.ldlt().solve(b);      // 注意这里的求解方式是ldlt分解
    double s = x(n_state - 1) / 100.0;  // 取出尺度
    ROS_DEBUG("estimated scale: %f", s);
    g = x.segment<3>(n_state - 4);      // 取出重力，从倒数第4个位置，取一个vector3d向量，正好把重力取出来
    ROS_DEBUG_STREAM(" result g     " << g.norm() << " " << g.transpose());

    // 做一些检查
    if(fabs(g.norm() - G.norm()) > 1.0 || s < 0)
    {
        return false;
    }

    // 重力修复：《VIO第7讲》 —— 视觉与IMU对齐流程中第4步：对重力向量g_c0进行优化
    RefineGravity(all_image_frame, g, x);

    // 得到真实尺度
    s = (x.tail<1>())(0) / 100.0;
    (x.tail<1>())(0) = s;
    ROS_DEBUG_STREAM(" refine     " << g.norm() << " " << g.transpose());
    if(s < 0.0 )
        return false;   
    else
        return true;
}

4、优化重力向量​​​​​​​

       两个问题：1、为什么需要优化重力向量？2、如何优化重力向量？

        考虑到上一步求得的g存在误差，一般认为重力矢量的模长是已知的，因此重力只剩下两个自由度，在切线空间上用两个变量重新参数化重力。

 

代码在initial_alignment.cpp文件中的RefineGravity()函数中，代码如下：

void RefineGravity(map& all_image_frame, Vector3d& g, VectorXd& x)
{
    // 参考论文
    Vector3d g0 = g.normalized() * G.norm();
    Vector3d lx, ly;
    //VectorXd x;
    int all_frame_count = all_image_frame.size();
    int n_state = all_frame_count * 3 + 2 + 1;

    MatrixXd A{n_state, n_state};
    A.setZero();
    VectorXd b{n_state};
    b.setZero();

    map::iterator frame_i;
    map::iterator frame_j;
    for(int k = 0; k < 4; k ++)
    {
        MatrixXd lxly(3, 2);
        lxly = TangentBasis(g0);    // // 重力向量优化，将重力向量参数化,这里是b1 b2纵着排列，形成的3×2矩阵
        int i = 0;
        for (frame_i = all_image_frame.begin(); next(frame_i) != all_image_frame.end(); frame_i++, i++)
        {
            frame_j = next(frame_i);

            MatrixXd tmp_A(6, 9);
            tmp_A.setZero();
            VectorXd tmp_b(6);
            tmp_b.setZero();

            double dt = frame_j->second.pre_integration->sum_dt;

            // 还是公式（17）,只不过优化变量由 g^c0 变为 w^c0  （公式21的转换）
            tmp_A.block<3, 3>(0, 0) = -dt * Matrix3d::Identity();
            tmp_A.block<3, 2>(0, 6) = frame_i->second.R.transpose() * dt * dt / 2 * Matrix3d::Identity() * lxly;    // 最后一项是[b1 b2]，注意优化的是w（需要求的是w向量，也就是b1和b2的参数 ）
            tmp_A.block<3, 1>(0, 8) = frame_i->second.R.transpose() * (frame_j->second.T - frame_i->second.T) / 100.0;     
            tmp_b.block<3, 1>(0, 0) = frame_j->second.pre_integration->delta_p + frame_i->second.R.transpose() * frame_j->second.R * TIC[0] - TIC[0] - frame_i->second.R.transpose() * dt * dt / 2 * g0;    // 公式（22）上半部分

            tmp_A.block<3, 3>(3, 0) = -Matrix3d::Identity();
            tmp_A.block<3, 3>(3, 3) = frame_i->second.R.transpose() * frame_j->second.R;
            tmp_A.block<3, 2>(3, 6) = frame_i->second.R.transpose() * dt * Matrix3d::Identity() * lxly;
            tmp_b.block<3, 1>(3, 0) = frame_j->second.pre_integration->delta_v - frame_i->second.R.transpose() * dt * Matrix3d::Identity() * g0;    // 公式（22）下半部分

            
            Matrix cov_inv = Matrix::Zero();
            //cov.block<6, 6>(0, 0) = IMU_cov[i + 1];
            //MatrixXd cov_inv = cov.inverse();
            cov_inv.setIdentity();

            MatrixXd r_A = tmp_A.transpose() * cov_inv * tmp_A;
            VectorXd r_b = tmp_A.transpose() * cov_inv * tmp_b;

            A.block<6, 6>(i * 3, i * 3) += r_A.topLeftCorner<6, 6>();
            b.segment<6>(i * 3) += r_b.head<6>();

            A.bottomRightCorner<3, 3>() += r_A.bottomRightCorner<3, 3>();
            b.tail<3>() += r_b.tail<3>();

            A.block<6, 3>(i * 3, n_state - 3) += r_A.topRightCorner<6, 3>();
            A.block<3, 6>(n_state - 3, i * 3) += r_A.bottomLeftCorner<3, 6>();
        }

        A = A * 1000.0;
        b = b * 1000.0;
        x = A.ldlt().solve(b);
        VectorXd dg = x.segment<2>(n_state - 3);        // 估计的w向量，也就是[b1 b2]的系数

        g0 = (g0 + lxly * dg).normalized() * G.norm();
        //double s = x(n_state - 1);
    }   
    g = g0;
}

5、求解世界坐标系w和初始相机坐标系c0之间的旋转矩阵q_wc0，并将轨迹对齐到世界坐标系下

 

 

这里还是沿用https://blog.csdn.net/jiweinanyi/article/details/99882311中的初始化思路：

1、上面的步骤已经根据旋转约束求出了陀螺仪bias bg，根据平移约束求出了gc0，s，和IMU坐标系下的速度Vs。

bool result = VisualIMUAlignment(all_image_frame, Bgs, g, x);
    if(!result)
    {
        ROS_DEBUG("solve g failed!");
        return false;
    }

2、获取所有图像帧中frame_count数量的的位姿Ps、Rs，并将其置为关键帧。

    for (int i = 0; i <= frame_count; i++)
    {
        Matrix3d Ri = all_image_frame[Headers[i].stamp.toSec()].R;
        Vector3d Pi = all_image_frame[Headers[i].stamp.toSec()].T;
        Ps[i] = Pi;
        Rs[i] = Ri;
        all_image_frame[Headers[i].stamp.toSec()].is_key_frame = true;
    }

3、根据三角化重新计算所有特征点的带尺度模糊的深度。

    //将所有特征点的深度置为-1
    VectorXd dep = f_manager.getDepthVector();
    for (int i = 0; i < dep.size(); i++)
        dep[i] = -1;
    f_manager.clearDepth(dep);
    //重新计算特征点的深度
    Vector3d TIC_TMP[NUM_OF_CAM];
    for(int i = 0; i < NUM_OF_CAM; i++)
        TIC_TMP[i].setZero();
    ric[0] = RIC[0];
    f_manager.setRic(ric);
    f_manager.triangulate(Ps, &(TIC_TMP[0]), &(RIC[0]));

4、优化后陀螺仪的偏置bg改变，重新进行预积分。

    for (int i = 0; i <= WINDOW_SIZE; i++)
    {
        pre_integrations[i]->repropagate(Vector3d::Zero(), Bgs[i]);
    }

5、将Ps、Vs、depth尺度s缩放后转变为相对于第0帧图像坐标系下。论文提到的以第一帧c0为基准坐标系，通过相机坐标系ck位姿得到IMU坐标系bk位姿的公式为：

        之前视觉SFM的结果都是以第l帧为关键枢纽帧（以第l帧为基准坐标系），转换到第一帧b0为基准坐标系的话应该是： 

for (int i = frame_count; i >= 0; i--)
    Ps[i] = s * Ps[i] - Rs[i] * TIC[0] - (s * Ps[0] - Rs[0] * TIC[0]);  

6、通过优化后的向量得到帧速度Vs和尺度s，去除深度值的尺度模糊。

    int kv = -1;
    map::iterator frame_i;
    for (frame_i = all_image_frame.begin(); frame_i != all_image_frame.end(); frame_i++)
    {
        if(frame_i->second.is_key_frame)
        {
            kv++;
            Vs[kv] = frame_i->second.R * x.segment<3>(kv * 3);
        }
    }
    for (auto &it_per_id : f_manager.feature)
    {
        it_per_id.used_num = it_per_id.feature_per_frame.size();
        if (!(it_per_id.used_num >= 2 && it_per_id.start_frame < WINDOW_SIZE - 2))
            continue;
        it_per_id.estimated_depth *= s;
    }

7、通过将重力旋转到z轴上，得到世界坐标系w与相机坐标系c0之间的旋转矩阵rot_diff。 

    Matrix3d R0 = Utility::g2R(g);    // 先得到u
    double yaw = Utility::R2ypr(R0 * Rs[0]).x();    // 再得到Θ
    R0 = Utility::ypr2R(Eigen::Vector3d{-yaw, 0, 0}) * R0;   // R_wc
    g = R0 * g;    // 将后面的gc0转换到世界坐标系下
    Matrix3d rot_diff = R0;

8、所有变量从参考坐标系c0转换到世界坐标系w。

    // Matrix3d rot_diff = R0 * Rs[0].transpose();
    Matrix3d rot_diff = R0;
    for (int i = 0; i <= frame_count; i ++)
    {
        Ps[i] = rot_diff * Ps[i];
        Rs[i] = rot_diff * Rs[i];   // 全部对齐到重力下，同时yaw角对齐到第一帧    R_w_ci = R_w_c0 * R_c0_ci
        Vs[i] = rot_diff * Vs[i];
    }