吴恩达机器学习课后作业7——K-means聚类与主成分分析

1. 问题和数据

在本练习中，您将实现K-means聚类算法并应用它来压缩图像。在第二部分中，您将使用主成分分析来寻找人脸图像的低维表示

之前的题目中都是有监督的算法，每一个样本X都对应有一个标签y,这回我们使用的K-means算法是无监督算法。其原理步骤如下：

   

2. 案例1：给定一个二维数据集，使用K-means算法进行聚类

数据集：ex7data2.mat

导入包，numpy和pandas是做运算的库，matplotlib是画图的库。
数据集是在MATLAB的格式，所以要加载它在Python，我们需要使用一个SciPy工具。

 

import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt

导入数据集 ，输出表头

data1 = sio.loadmat('ex7data2.mat')
print('data1.keys():', data1.keys())

输出表头，会发现数据集里只有X，没有标签y了

data1.keys(): dict_keys(['__header__', '__version__', '__globals__', 'X'])

再取出X，打印X的shape出来看一看

X = data1['X']
print('X.shape', X.shape)  # X是一个有300行（样本），两列（特征）的数据

输出结果：

X.shape (300, 2)

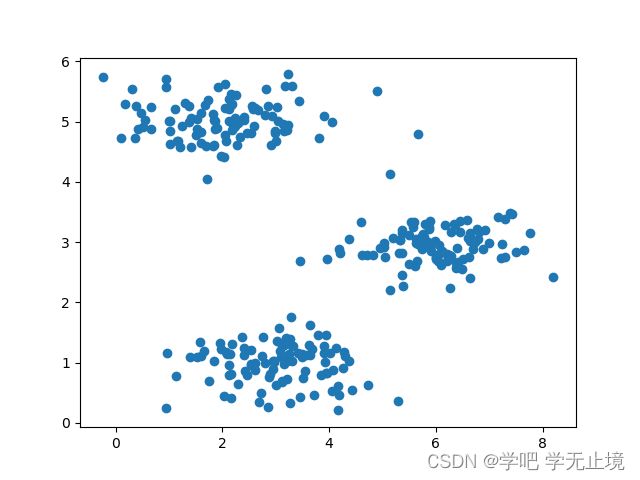
画出散点图看看

plt.scatter(X[:, 0], X[:, 1])
plt.show()

X数据的散点图：

 

获取每个样本所属的类别

def find_centrolds(X, centros):
    idx = []

    for i in range(len(X)):
        # X是一个一维数组，centros是一个二维数组（k,2），k表示类别数；
        # print('X[i]:', X[i])
        dist = np.linalg.norm((X[i] - centros), axis=1)  # axis=1是按列；# np.linalg.norm线性带代数库的norm二范数，其实就是开方；
        # 得到每一个i下对应得有三个dist
        # print('dist:', dist)
        # print('dist.shape:', dist.shape)
        id_i = np.argmin(dist)  # 找到dist里当前i时最小的,让它等于id_i
        idx.append(id_i)  # 再将id_i给append到idx里

    return np.array(idx)   # 将idx以数组形式返回

centros = np.array([[3, 3],[6, 2], [8, 5]])  # 给定一个三行两列的centros，表示为将我们的数组化为一个3维的标签，标签值分别为0，1，2；其实就是数据会聚成三个类，这三个数据是up主自己随便选择的
idx = find_centrolds(X, centros)  # 调用find_centrolds函数
print('idx[:3]:', idx[:3])

输出结果：

idx[:3]: [0 2 1]

运行kmeans,重复执行1和2

def run_kmeans(X, centros, iters):

    k = len(centros)
    centros_all = []
    centros_all.append(centros)
    centros_i = centros

    for i in range(iters):
        idx = find_centrolds(X, centros_i)
        centros_i =compute_centros(X, idx, k)
        centros_all.append(centros_i)

    return idx, np.array(centros_all)

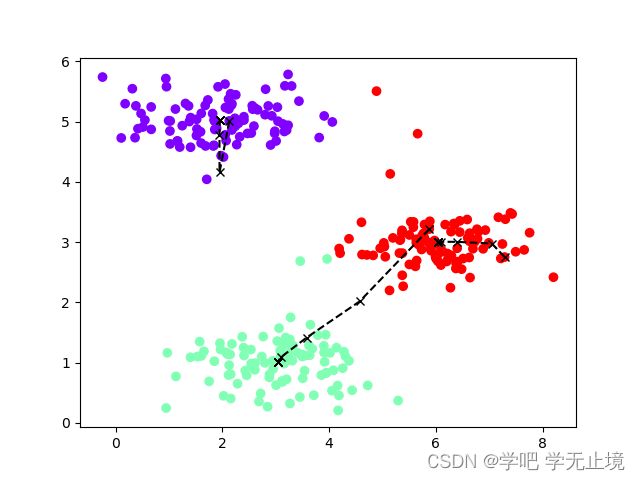
为了更直观的看到变化过程，绘制数据集和聚类中心的移动轨迹：

def plot_data(X, centros_all, idx):
    plt.figure()
    plt.scatter(X[:, 0], X[:, 1], c=idx, cmap='rainbow')  # cmap是配色盘
    plt.plot(centros_all[:, :, 0], centros_all[:, :, 1], 'kx--')  # centros_all是一个三维数组，第一维度是迭代次数，然后是类别数，特征数

idx, centros_all = run_kmeans(X, centros, iters=10)
plot_data(X, centros_all, idx)
plt.show()

重复运行了3次，绘制出的3个图：

 

 

 

3. 案例2：给定一个二维数据集，使用K-means算法进行聚类

参考文献：
[1] https://www.bilibili.com/video/BV1p4411o7sq?p=6&spm_id_from=pageDriver&vd_source=72e4369cf6b54497a1e04f2071a47a1e