python气象数据处理——计算台风方位角平均物理量

研究台风的同学们应该都接触过需要计算以台风为中心的方位角平均物理量，这就需要将笛卡尔坐标系中的数据插值到极坐标系，再对各个方位角的数据进行平均。最近在学习Python，相比NCL和FORTRAN，Python程序更为简洁，可以调用很多现成的库，最后插值效果也还不错。

以ERA5数据为例，给定一个台风中心，选取层次为500 hPa，进行插值计算：

#用到的库
from scipy import interpolate #用来插值
import metpy.calc as mpcalc   #常用气象物理量计算的库
from metpy.units import units  
import xarray as xr   
import numpy as np 

def main():   
    
    #nc数据读取
    ds = xr.open_dataset('data.nc')
    lat = ds.latitude
    lon = ds.longitude
    time = ds.time
    
    #这边以一个时次、单层为例，lon_t,lat_t是台风中心位置
    uwnd = ds['u'].sel(time = time[0],level= 500)
    lon_t=128.9
    lat_t=20.0

    #azimuths是极坐标系中的角度，ranges是半径，可以根据自己需要设置
    azimuths = np.linspace(0,360,73)*units.degree
    ranges = np.linspace(0,1000,101)*1000*units.meter
 
    #利用metpy库可以十分便捷的得到插值后的经纬度坐标
    lon_a,lat_a = mpcalc.azimuth_range_to_lat_lon(azimuths,ranges,lon_t,lat_t)

    #因为ERA5的数据分辨率是0.25°，为了保证插值后不产生NAN，边界上各扩大一个格点
    lons = lon[(lon>=lon_a.min()-0.25) & (lon<=lon_a.max()+0.25)] 
    lats = lat[(lat>=lat_a.min()-0.25) & (lat<=lat_a.max()+0.25)]

    #构造插值前的格点矩阵
    lon_s,lat_s = np.meshgrid(lons,lats)
    grid_in = np.concatenate([lon_s.reshape(-1,1), lat_s.reshape(-1,1)], axis=1)
    grid_out = np.concatenate([lon_a.reshape(-1,1), lat_a.reshape(-1,1)], axis=1)

    #这边以变量u为例，进行插值
    u_in = uwnd.sel(longitude=lons,latitude=lats)
    u_out = interpolate.griddata(grid_in, np.array(u_in).flatten(), grid_out, method='cubic')
    u_out = u_out.reshape((len(azimuths),len(ranges)))

    #画填色图检验插值数据
    fig = plt.figure(figsize=(11,4))
    fig1 = plt.subplot(1, 2, 1) 

    #插值前的u
    c_f1 = plt.contourf(lons, lats, u_in, np.arange(-12,6,2), cmap='bwr', extend='both')
    plt.title('u_wind in original data')
    plt.scatter(lon_t,lat_t, s=150, marker=get_hurricane(),
        edgecolors="black", linewidth=2.3,zorder=3)

    fig2 = plt.subplot(1, 2, 2) 
    
    #插值后的u
    c_f2 = plt.contourf(lons, lats, u_out, np.arange(-12,6,2), cmap='bwr', extend='both')
    plt.title('u_wind after interpolation')
    plt.scatter(lon_t,lat_t, s=150, marker=get_hurricane(),
        edgecolors="black", linewidth=2.3,zorder=3)

    #色标的设置
    cbar = plt.colorbar(c_f1,orientation='vertical',shrink=0.75)    
    cbar.ax.tick_params(labelsize='12')

    plt.show()
                    

if __name__ == "__main__":
    main()

得到插值前后变量u的对比图：

 可以看到插值效果还是十分不错的。

插值后的数据是方位角和半径的函数，接下来就可以利用插值后的数据进行方位角平均，这里介绍最常用的切向风与径向风的计算：

#分别对变量u和v进行插值
u_in = ds['u'].sel(longitude=lons, latitude=lats)
v_in = ds['v'].sel(longitude=lons, latitude=lats)
u_out = interpolate.griddata(grid_in, np.array(u_in).flatten(), grid_out, method='cubic')
v_out = interpolate.griddata(grid_in, np.array(v_in).flatten(), grid_out, method='cubic')
u_out = u_out.reshape((len(azimuths),len(ranges)))
v_out = v_out.reshape((len(azimuths),len(ranges)))

#计算切向风、径向风
vt = np.zeros((len(azimuths),len(ranges)))
vr = np.zeros((len(azimuths),len(ranges)))
for k in range(0,len(azimuths)):
    for l in range(0,len(ranges)):
        vt[k,l]=v_out[k,l]*np.cos(azimuths[k]*np.pi/180)-u_out[k,l]*np.sin(azimuths[k]*np.pi/180)
        vr[k,l]=u_out[k,l]*np.cos(azimuths[k]*np.pi/180)+v_out[k,l]*np.sin(azimuths[k]*np.pi/180)  
      
#计算方位角平均
vt_am = np.mean(vt,axis=0)
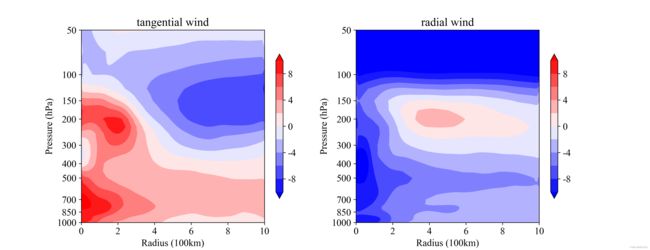
vr_am = np.mean(vr,axis=0)

对多层数据进行计算后，可以得到方位角平均的半径-气压剖面图：

 

 这两张图可以清楚的给出台风切向风与径向风的垂直分布特征。