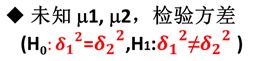SPSS-参数检验
1. 假设检验
假设检验分为参数检验与非参数检验。
(1) 参数检验:已知总体分布, 猜测总体的某参数(原假设H0,null hypothesis),用一组样本来检验这个假设, 是否正确 (即接受还是拒绝假设H0)。
(2) 非参数检验:两总体的分布未知,检验两总体分布是否一致(用两组样本来检验);由样本分布推测其总体分布 (假设H0),用另一组样本来检验这个假设,是否正确。
1.1. 正态总体下的参数假设检验
前提:总体分布为正态分布。

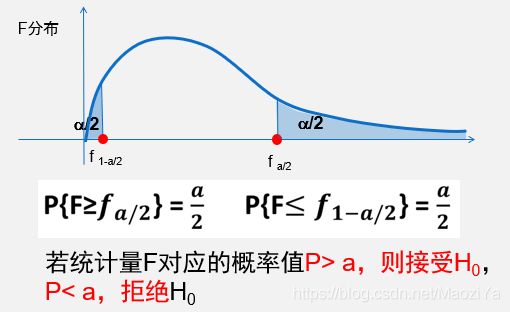
若计算出Z统计量的区间估计在(-k,k)之间,同时设定一个置信度(1-a)%, 找出该置信度下置信区间【-Za/2, Za/2 】。若(-k,k)在【-Za/2, Za/2 】内,接受假设H0。否则,则拒绝假设H0。
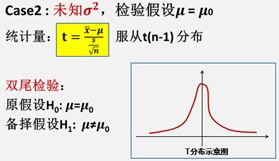
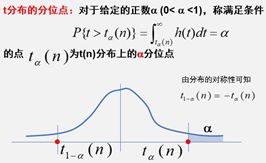
临界值法:设置显著性水平为a,则统计量| t | <= t_a/2,则接受假设H0;否则拒绝原假设H0。
等价判断(P-值法):t对应的p>=a,则接受假设H0,否则,拒绝假设H0。

应用:假设检验在管理,社会科学乃至所有用到统计方法的自然科学中,有广泛的应用。例如,
- 改变工艺或配方,是否提高了平均效率?
- 培训前后,是否提高了技术水平,效率,智商?
注意:改变与否都是从平均的角度来看的。其特点是面向某个均值指标,采取某项措施前后的比较。
1.2. SPSS 单样本T检验 One-Sample T Test
单样本T检验的目的是利用来自某总体的样本数据,推断该总体的均值是否与指定的检验值之间存在显著差异。是对总体均值的假设检验。
问题描述:已知总体服从正态分布(先决条件),通常总体方差也未知,由独立单样本推断总体的均值是否为指定的检验值。
Ex1:已知某小学5年级学生400米的历年平均成绩为100秒,今测得60个小学5年级学生的400米成绩,检验该校5年级学生的400米成绩是否有变化。
数据:“Chapter4-2-小学生400米成绩.sav”
检验假设:H0: m =100,即成绩仍保持为100秒;备择假设H1: m ≠100平均成绩有显著变化。
注意需要设置检验值,表示与均值100进行比较。
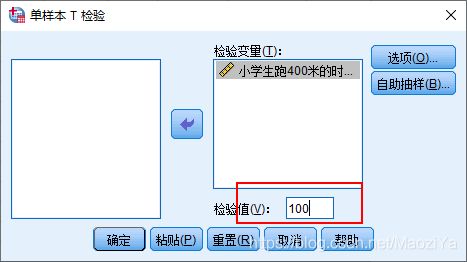
原先成绩为100秒,样本均值Mean = 105.3850,是否说明该校5年级学生的400米成绩降低了?
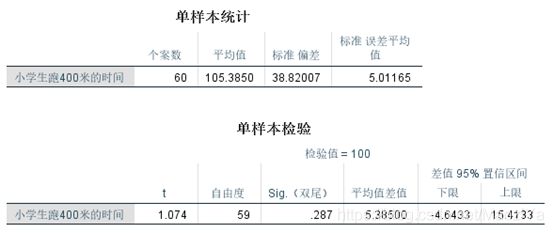
由上表,t(59) = 1.074, p=0.287 > 0.05 ,说明在95%的置信区间内,总体均值与100无显著差异,该校小学生400米成绩仍保持在100秒.
Lower和Upper 表明95%的置信区间的两个端点,离总体均值100的距离分别是 (-4.8433,15.4133).
点估计100+5.385 = 105.385;区间估计[100-4.8433,100+15.4133]。说明区间或高于100,或低于100,因此可能与原来的100秒无差异。
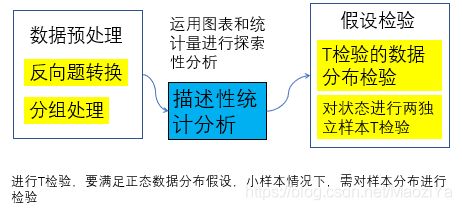
注意:进行T检验前需要先进行数据正态分布检验。符合正态分布的数据才适合进行T检验。
1.3. 两个正态总体下的参数检验
研究两个相互独立的正态总体的参数检验问题。
应用:两个正态总体的参数比较问题,特别是均值比较问题在管理科学乃至整个社会科学中有着广阔的应用。例如,
-
两台设备生产的产品的某种性质
-
两种工艺的某种性能
-
两种治疗方法的效果
-
两种政策(税收,投资等)的比较等。
表示效果,性质的指标多种多样,应用面十分广泛。
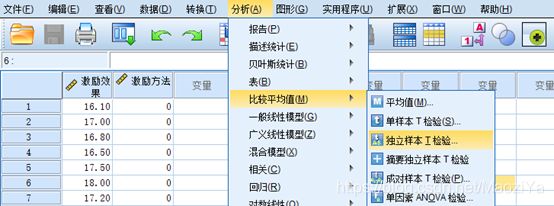
1.4. SPSS 相互独立的两组样本的T检验 Independent-Sample T test
检验目的:利用来自某两个总体的独立样本,推断两个总体的均值是否存在显著差异。
要求:样本来自的总体服从正态分布,两组样本相互独立,即从一总体中抽取一组样本对从另一总体中抽取一组样本没有任何影响,两组样本的个案数可不相等。
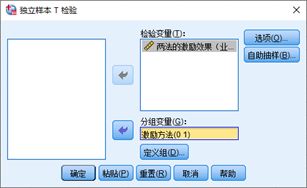
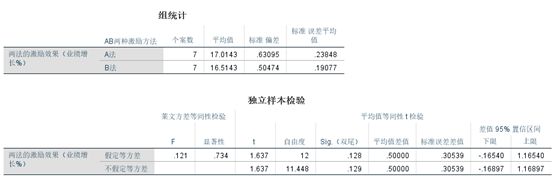
Ex. 用两种激励方法A和B,对用同样工种的两个班组进行激励,每个班组7人,测得激励后业绩的增长率(%).问:两种激励措施的平均激励效果有无差异?
方差齐次检验,F = 0.121,p = 0.734 > 0.05, 接受H0,说明方差齐次。
方差齐次条件下进行均值检验,t(12) = 1.637, p = 0.128 > 0.05, 说明,接受H0:
![]()
,即两种激励方法的效果无明显差异。
1.5. SPSS 配对样本的T检验 Paired-Sample T test
配对样本指抽样不是相互独立而是相互关联的。如个案在“前”“后”两种状态下某种属性的两种状态,也可以是对某事物两个不同侧面或方面的描述。
基本特征:两组样本的样本数相同;两组样本观察值的先后顺序一一对应。
假设检验:H0:两总体均值无显著差异,即
![]()
统计量:t 统计量
间接通过单样本t检验实现。先对两组样本分别计算出每对观察值的差值得到差值样本;然后,利用差值样本,通过对其均值是否显著为0的检验来推断两总体均值的差是否显著为0. 因此要求观察数据数据相同且次序不可随意改动,即所谓的配对样本。
Ex2:减肥茶效果检验。为研究某种减肥茶是否具有明显的减肥效果,某健身机构对35名志愿者进行了减肥跟踪调研。首先将其喝减肥茶以前的体重记录下来,三个月后再依次将这35名志愿者喝茶后的体重记录下来。通过这两组样本数据的对比分析,推断减肥茶是否有明显的减肥效果?
体重近似认为服从正态分布。实验前后获得的样本数据为配对样本。因此采用两配对样本t检验的方法,通过检验喝茶前后体重的均值是否发生显著变化来确定减肥茶的减肥效果。
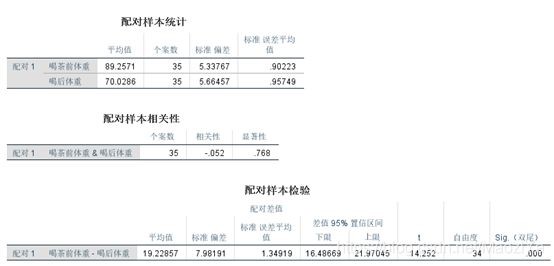
喝茶前后体重的均值有较大差异。喝茶后的平均体重70.0286低于喝茶前89.2571的平均体重。
由表可知,T(34) =14.252,p= 0.0<0.05,拒绝H0,即认为总体上体重变化均值与0有显著差异,意味着喝茶前后体重均值存在显著差异,该茶有减肥效果。
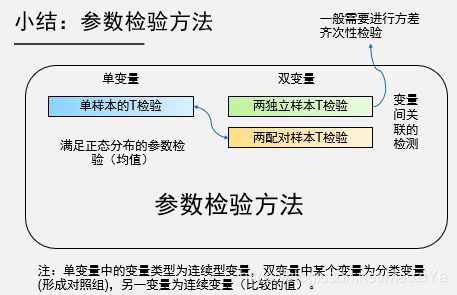
1.6. 总结
2. 练习:案例I_工作认可度与工作态度
数据:“Chapter4-2-参数检验-工作压力调查(已处理).sav”
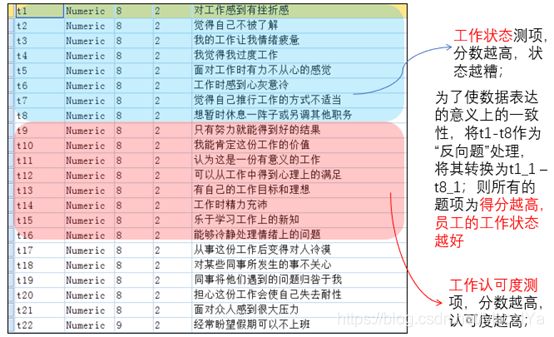
受访对象对每道测项题的回答:各人的感知状态,相当于4度的量表。
问题描述:利用某机构工作人员对自己工作看法的调查数据,借助项目分析法的核心思想,研究工作人员对自己工作的不同认可程度是否会影响工作状态。
分析方法:
-
描述性统计方法(探索性研究):分组箱线图
-
参数检验(两独立样本T检验)
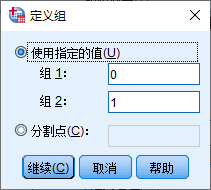
分析思路:将认尺度变量离散化,构造分类变量;将工作认可度按照得分进行分组,形成高分组和低分组
目标问题:不同分组的员工的工作状态是否存在显著差异?若存在显著差异,则说明工作认可度对工作态度关联密切。
方法:两独立样本T检验