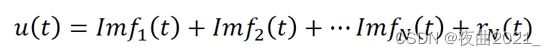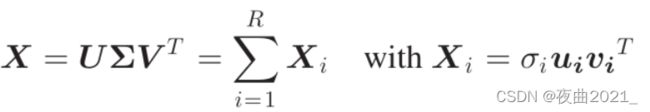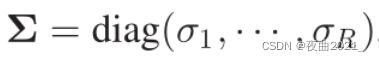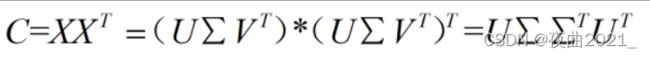非平稳信号的自适应分解算法：EMD、SSA、ITD、VMD以及其变体之间的总结与对比

目录

一、EMD

1.算法步骤：

2.算法优点： 

 3.算法缺点及其解决方法

4.EMD算法的变体:主要针对EMD的模态混叠问题提出的

二、SSA

1.算法步骤：

2.算法优点：

3.算法缺点及其解决方法

 4.SSA算法的变体：

---

一、EMD

经验模态分解（Empirical Mode Decomposition,EMD）

原文：

 N.E. Huang, Zheng Shen, Steven R. Long, et al, The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series
analysis, Proc. R. Soc. Lond. A 454 (1998) 903–995.

1.算法步骤：

（1）.计算原始信号x(t)的极值点，然后使用三次样条插值根据极值点计算非平稳信号的上下包络线，并计算上下包络线的均值

（2）.用原始信号x(t)减去上下包络线的均值，得到的信号h(t1)判断是否满足本征模态函数IMFs的两个条件：①极值点和零点的数目差不超过1，②上下包络函数的均值为0。

若不满足，则继续求h(t1)的上下包络线的均值，然后用h(t1)减去均值，得到h(t2)并判断h(t2)是否满足IMFs的两个条件，直至满足条件，得到第一个IMF1。

若满足，令其为IMF1，然后用原始信号x(t)减去IMF1，得到信号继续判断是否满足IMFs的条件。

通过以上迭代过程，可得到若干个IMFs，直至剩下单调信号分量。

2.算法优点： 

        针对非平稳信号，第一次提出分解的思想，将信号分量与噪声分量自动分离，选择需要的信号分量重构，可实现去噪的目的。

 3.算法缺点及其解决方法

①端点效应：上下包络线是根据信号极值点信息使用三次样条插值求得的，但是不能保证信号的左右端点恰好是局部极值，这样，信号的上下包络线在端点处会产生大的波动，分解出的本征模态函数失真，随着分解的进行，这种失真现象由外向内扩散，直至“污染”整个本征模态函数。

解决方法：多项式拟合延拓法、匹配延拓法、极值点对称延拓法、镜像闭合延拓法等

②模态混叠：不同模态的信号混叠在一起，一般有两种情况：一是不同特征尺度的信号在一个IMF分量中出现，另一种是同一个特征尺度的信号被分散到不同的IMF分量中。

4.EMD算法的变体:主要针对EMD的模态混叠问题提出的

（1）.EEMD：集成经验模态分解(Ensemble empirical mode decomposition)

                原文：Wu, Z., and N. E. Huang, 2009, Ensemble empirical mode decomposition: Anoise-assisted data analysis method: Advances in Adaptive Data Analysis,01, 1–41

EEMD是每次分解前都对原信号加入白噪声，然后再进行分解。重复多次后，取平均IMFs，缺点是由于加入了噪声，重构信号不准确。且计算非常耗时，不适用于实时分解

（2）.CEEMD：Complementary EEMD（谷歌学术引用量800+）

        原文：COMPLEMENTARY ENSEMBLE EMPIRICAL MODE DECOMPOSITION: A NOVEL NOISE ENHANCED DATA ANALYSIS METHOD.DOI: 10.1142/S1793536910000422

算法内容：

        CEEMDAN：（谷歌学术引用量1300+）

原文：A complete ensemble empirical mode decomposition with adaptive noise:Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing ，2011

改进内容：在第一个筛选阶段加入适当的白噪声，后续分解出来的模态再继续加白噪声

（3）.ICEMMD：improve CEEMD

        原文：Colominas, M. A., G. Schlotthauer, and M. E. Torres, 2014, Improved complete ensemble EMD: A suitable tool for biomedical signal processing 

二、SSA

        奇异谱分析(Singular Spectrum Analysis, SSA)是一种处理非线性时间序列数据的方法，通过对所要研究的时间序列的轨迹矩阵进行分解、重构等操作，提取出时间序列中的不同成分序列(长期趋势，季节趋势，噪声等)，从而进行对时间序列进行分析或去噪并用于其他一些任务。

原文：

Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series

R Vautard, M Ghil-Physica D: Nonlinear Phenomena, 1989 - Elsevier

1.算法步骤：

        主要包括四个步骤：嵌入——分解——分组——重构。

有博主已经整理的很好了

参考文章链接：https://blog.csdn.net/Lucky_Go/article/details/103109045

步骤1：嵌入

对于一个一维N个采样点的时间序列：选择窗口长度L生成滞后矩阵X：

 其中L(属于区间[2，N-1])的选择很重要，影响最终的分解效果。

步骤2：奇异值分解

对矩阵X进行奇异值分解：

 其中为对角矩阵，为降序排列的奇异值，ui和vi分别是对应于正交矩阵U和V的列的左奇异向量和右奇异向量。

 由于直接计算X的奇异值分解不好计算，因此先对其协方差矩阵C进行奇异值分解：

 则其第i个奇异值等于

 可得到矩阵C的奇异值和对应的特征向量U1,U2......Un：

 矩阵V便可根据两边同时取转置计算出来。注意U,V都是正交矩阵，即转置矩阵等于其逆矩阵，为对角矩阵，其逆矩阵为对角线上的数取倒数：

步骤3：分组

步骤4：对角线平均（重构）

2.算法优点：

        SSA是无模型的，对时间序列既不要求平稳，又不假设参数模型，可广泛应用于各种时间序列。

3.算法缺点及其解决方法

        SSA最关键的步骤是对轨迹矩阵进行SVD分解，然后可根据奇异值大小来判断对应的分量为信号分量还是噪声分量。奇异值越大的越代表信号分量。问题就在于如何确定一个阈值区分信号分量和噪声分量。

 4.SSA算法的变体：

（1）.truncated SVD (TSVD)：截断SVD

参考文献：

        此方法根据介于0和1之间的预定义百分比阈值直接截断奇异值。实际计算时，它测试从第一个特征值中累积的临时特征值是否大于或等于该阈值乘以所有特征值之和，然后，将小特征值设置为0以实现降秩。

        缺点是这种方法需要根据经验预先定义窗口长度和阈值。

（2）.singular value thresholding (SVT) ：奇异值阈值法

参考文献：

        该方法将降阶视为一个优化问题。优化问题的目标函数是最小化未知低秩信号矩阵和噪声观测特征向量加权组合建模的去噪信号矩阵之间的矩阵Frobenius范数。  权重的数量被设置为信号矩阵的秩。此外，通过OptShrink算法可以获得最优权重 。

        缺点是此方法需要预先知道信号轨迹矩阵的秩，这是很难做到的。此外计算耗时大。   

（3）.Multistage Singular Spectrum Analysis：多级SSA

参考文献：Weichao Kuang , Shanjin Wang.Efficient and Adaptive Signal Denoising Based on Multistage Singular Spectrum Analysis.IEEE TRANSACTIONS ON INSTRUMENTATION AND MEASUREMENT, VOL. 70, 2021

算法步骤：

 三、ITD

固有时间尺度分解（Intrinsic time-scale decomposition）可将非平稳信号自适应的分解为一系列固有旋转分量（proper rotation components）之和。

原文：Intrinsic time-scale decomposition: time–frequency–energy analysis and real-time filtering of non-stationary signals. MARK G. FREI, IVAN OSORIO.