Python数据分析入门--SciPy库学习笔记
文章目录
- 前言
- Scipy库简单入门
-
- 1.cluster模块
- 2. constants模块
- 3. fftpack模块
- 4. integrate 模块
- 5. interpolate 模块
- 6. linalg模块
- 7. ndimage模块
- 8. optimize模块
- 9. stats模块
- 10. ord模块
- 总结
前言
scipy是一个python开源的数学计算库,可以应用于数学、科学以及工程领域,它是基于numpy的科学计算库。主要包含了统计学、最优化、线性代数、积分、傅里叶变换、信号处理和图像处理以及常微分方程的求解以及其他科学工程中所用到的计算
scipy主要通过下面这些包来实现数学算法和科学计算:
| 子模块 | 描述 |
|---|---|
| cluster | 包含聚类算法,向量计算 |
| constants | 物理和数学上的一些常数 |
| fftpack | 快速傅里叶变换 |
| integrate | 积分和常微分方程的求解 |
| interpolate | 插值和平滑的样条函数 |
| io | 输入和输出 |
| linalg | 线性代数 |
| ndimage | N维的图像处理 |
| odr | 回归正交距离 |
| optimize | 优化和寻根方程 |
| signal | 信号处理 |
| spatial | 空间数据结构和算法 |
| sparse | 稀疏矩阵 |
| special | 特殊的函数 |
| stats | 统计分布和函数 |
Scipy库简单入门
1.cluster模块
聚类分析是在数据中发现数据对象之间的关系,将数据进行分组,组内的相似性越大,组间的差别越大,则聚类效果越好。聚类分析常用的距离度量有欧式距离、曼哈顿距离、切比雪夫距离和明可夫斯基距离等。
K均值聚类是一种在一组未标记数据中查找聚类和聚类中心的方法。 直觉上,我们可以将一个群集(簇聚)看作一组数据点,其点间距离与群集外点的距离相比较小。 给定一个K中心的初始集合,K均值算法将重复以下步骤
- 选择 K 个初始质心(K需要用户指定),初始质心随机选择即可,每一个质心为一个类
- 对剩余的每个样本点,计算它们到各个质心的欧式距离,并将其归入到相互间距离最小的质心所在的簇,计算各个新簇的质心。
- 在所有样本点都划分完毕后,根据划分情况重新计算各个簇的质心所在位置,然后迭代计算各个样本点到各簇质心的距离,对所有样本点重新进行划分
- 重复2. 和 3.,直到质心不在发生变化时或者到达最大迭代次数时
from scipy.cluster.vq import kmeans,vq,whiten
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(30,30))
ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,2)
data1 = np.random.rand(10,3) + np.array([.5,.5,.5])
data2 = np.random.rand(10,3)
data = np.vstack((data1,data2))
data = whiten(data)
centre,_ = kmeans(data,3)
cluster,_ = vq(data,centre)
ax1.scatter(data1,data2)
a = [] # 下面都是数据可视化操作
b = []
c = []
for i in range(len(cluster)):
if cluster[i] == 0:
a.append(data[i])
elif cluster[i] == 1:
b.append(data[i])
else:
c.append(data[i])
xx = []
for i in range(3):
xx.append([])
# 样本数据纵坐标列表
yy = []
for i in range(3):
yy.append([])
m = []
m = [a, b, c]
for i in range(3):
for j in range(len(m[i])):
xx[i].append(m[i][j][0])
for j in range(len(m[i])):
yy[i].append(m[i][j][1])
ax2.scatter(xx[i], yy[i], label=i)
plt.legend()
plt.show()
print(data)
print('\n')
print(centre)
print('\n')
print(cluster)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code8.py
[[1.14865697 2.69405034 1.73788065]
[3.23341434 3.23294749 3.53956713]
[3.2839023 3.59125444 3.9455198 ]
[2.51874233 2.77678538 1.57993031]
[2.17842407 1.75756848 3.80120161]
[2.10036682 2.59059014 1.83130737]
[2.78107445 2.77670545 3.22940596]
[2.18464206 2.80216035 2.46133769]
[2.0737308 2.41947047 1.83787354]
[2.95571045 4.05702503 3.41077657]
[1.50081545 1.93798131 1.78342349]
[0.77652033 2.22745268 1.39755954]
[0.05806498 1.22388636 0.87025516]
[0.71156678 2.42998927 2.58839209]
[0.36591912 0.31864204 2.4776798 ]
[0.30741828 0.67968106 1.47645486]
[0.46902599 0.56745425 0.17545723]
[1.25626675 1.47109371 1.57507801]
[0.93078627 2.6552914 1.28276725]
[2.05924502 0.9403261 2.88461438]]
[[0.30010709 0.69741593 1.24996176]
[1.56921269 2.26774465 1.90546948]
[2.88650512 3.08310018 3.58529421]]
[1 2 2 1 2 1 2 1 1 2 1 1 0 1 0 0 0 1 1 1]
#Process finished with exit code 0
k-means算法的实例说明
假定某共用办公室有两个人使用,他们使用办公室的时候都会用空调遥控器设置房间的温度。但空调遥控器显示面板坏掉了,只能通过加减温度的方式盲调整。但已知他们习惯的温度不同。办公室的温度计有记录功能,每天记录12 小时的温度,每15 分钟记录一次,根据一个月所记录的数据,通过聚类算法,算出这两个人的喜好温度,并估算他们各使用办公室多少时间。可以认为这两个人使用办公室的时候室内温度是不同方差和不同均值的正态分布随机数,生成模拟数据,并用matplotlib 画出数据的直方图。使用K 均值聚类算法将模拟数据分成两个簇,两个簇的最佳温度为两人需要的空调温度,通过预判每个人使用办公室的时间来实现空调调温自动化。
2. constants模块
Scipy的constants模块是一个包含大量的数学和物理常量的库,可用于一般科学领域
import scipy.constants
print(scipy.constants.pi)
print('\n')
print(scipy.constants.speed_of_light)
print('\n')
print(scipy.constants.Planck)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code4.py
3.141592653589793
299792458.0
6.62607015e-34
#Process finished with exit code 0
下面是一些常见的数学和物理常量汇总
| 数学常量 | 描述 |
|---|---|
| pi | 圆周率 |
| golden | 黄金比例 |
| 物理常量 | 描述 |
|---|---|
| speed_of_light | 真空中的光速 |
| mu_0 | 磁常数 |
| epsilon_0 | 真空介电常数 |
| Planck | 普朗克常数 |
| G | 万有引力常数 |
| g | 标准重力加速度 |
| e | 基本电荷 |
| gas_constant | 摩尔气体常数 |
| fine_structure | 精细结构常数 |
| N_A | 阿伏伽德罗常数 |
| Boltzmann | 玻尔兹曼常数 |
| Stefan_Boltzmann | 斯蒂芬-玻尔兹曼常数 |
| m_e | 电子质量 |
| m_p | 质子质量 |
| m_n | 中子质量 |
3. fftpack模块
在数学中,傅里叶级数(Fourier series)是把类似波的函数表示成简单正弦波的方式。更正式地说法是,它能将任何周期性函数或周期信号分解成一个(可能由无穷个元素组成的)简单振荡函数的集合,即正弦函数和余弦函数。
傅里叶变换是一种数学变换,它将一个函数(通常是一个时间的函数,或一个信号)分解成它的组成频率,例如用组成音符的音量和频率表示一个音乐和弦。其本质是一种线性积分变换,用于信号在时域(或空域)和频域之间的变换,在物理学和工程学中有许多应用。实际上傅里叶变换就像化学分析,确定物质的基本成分;信号来自自然界,也可对其进行分析,确定其基本频率成分。
快速傅立叶变换(FFT)是一种计算数字信号序列的离散傅立叶变换(DFT)或其逆变换(IDFT)的算法。傅里叶分析将信号从其原始域(通常是时间或空间)转换为频域的表示,反之亦然。DFT是通过将一系列值分解成不同频率的分量来获得的。这个操作在很多领域中都很有用,但是直接从定义中计算它通常太慢而不实际。FFT通过将DFT矩阵分解成稀疏(大部分为零)因子的乘积来快速计算这种转换。所以其本质是实现离散傅立叶变换的一种优化算法,将时间复杂度从O(N^2)降低为O(NlogN),其中N为待计算序列的长度。当N非常大时,这中优化在时间维度上提升是非常显著的。
傅里叶变换广泛应用于信号和噪声处理,图像处理,音频信号处理等领域,比如51单片机会利用快速傅里叶变换来实现滤波。SciPy提供fftpack模块,可让用户计算快速傅立叶变换。
import numpy as np
from scipy import fftpack
time_step = 1
period = 5.
time_vec = np.arange(0, 20, time_step)
sig = np.sin(2 * np.pi / period * time_vec) + 0.5 *np.random.randn(time_vec.size)
print(sig.size)
print('\n')
print(sig)
print('\n')
sample_freq = fftpack.fftfreq(sig.size, d = time_step)
sig_fft = fftpack.fft(sig)
print(sig_fft)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code4.py
20
[ 0.8619723 0.80046426 1.47924167 -0.75314181 -1.25099334 0.51117803
1.74449108 2.02777642 -0.82128671 -0.45706612 -0.5045473 0.30284392
0.30628348 -1.33838885 -0.7817602 0.16376441 0.84729352 -0.1188564
-0.45284573 -0.82521711]
[ 1.74120551 -0.j 1.39666054 -3.7049906j
-0.7001181 +2.21076727j 3.55673302 -1.71079756j
0.88382092-10.81685692j -1.54131028 +1.5186949j
-0.65092151 +1.57638056j 0.43460041 -0.68361725j
0.82649494 +2.59411121j 2.98591428 -1.9451872j
1.11449199 -0.j 2.98591428 +1.9451872j
0.82649494 -2.59411121j 0.43460041 +0.68361725j
-0.65092151 -1.57638056j -1.54131028 -1.5186949j
0.88382092+10.81685692j 3.55673302 +1.71079756j
-0.7001181 -2.21076727j 1.39666054 +3.7049906j ]
#Process finished with exit code 0
我们通过上述程序利用非正弦波模拟一个嘈杂的输入信号,fftfreq函数将生成采样频率,然后利用fft函数计算快速傅里叶变换。
4. integrate 模块
高等数学里的大量的积分都是可以被分析积分的,但生活中有很多积分是我们不可积的。当一个函数不能被分析积分,或者很难分析积分时,通常会转向数值积分方法。 SciPy有许多用于执行数值积分的程序。 它们中的大多数都在同一个scipy.integrate库中
import scipy.integrate
import numpy as np
g = lambda x:np.cosh(x)
f = lambda x:np.exp(-x**2)
a = scipy.integrate.quad(f, 0, 2)
b = scipy.integrate.quad(g, 0, 2)
print(a)
print('\n')
print(b)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code6.py
(0.8820813907624215, 9.793070696178202e-15)
(3.6268604078470186, 4.0266239318931457e-14)
#Process finished with exit code 0
积分函数会返回两个值,其中第一个数字是积分值,第二个数值是积分值绝对误差的估计值。后面我们还会接触到多重积分,二重积分可以理解为求一个的物体体积(高对底面积的积分),三重积分可以理解为求一个密度分布不均匀物体的质量(密度函数对体积的积分),二重和三重积分的机制已被包含到函数dblquad,tplquad和nquad中。,这些函数分别需要四个或六个参数。
import scipy.integrate
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.ticker as ticker
from matplotlib.ticker import MultipleLocator
fig = plt.figure(figsize=(30,30))
ax = Axes3D(fig)
g = lambda x, y: x**2 + y**2
f = lambda x: 0
l = lambda y: 0
x = np.arange(1, 2, 0.05)
y = np.arange(1, 2, 0.05),
x, y = np.meshgrid(x, y)
z = x**2 + y**2
a = scipy.integrate.dblquad(g, 1, 2, 1, 2)
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow')
plt.show()
print(a)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code6.py
(4.666666666666666, 7.021774688857003e-14)
#Process finished with exit code 0
dblquad函数的一般形式包含五个参数(func,a,b,gfun,hfun)。 其中,func是要积分函数的名称,'a’和’b’分别是x变量的下限和上限,而gfun和hfun是定义变量y的下限和上限的函数名称。以下是常用函数
| 函数名称 | 描述 |
|---|---|
| quad | 一重积分 |
| dblquad | 二重积分 |
| tplquad | 三重积分 |
| nquad | n重积分 |
| fixed_quad | 高斯积分,阶数n |
| quadrature | 高斯正交到容差 |
| romberg | Romberg积分 |
| trapz | 梯形规则 |
| cumtrapz | 梯形法则累计计算积分 |
| simps | 辛普森规则 |
| polyint | 分析多项式积分 |
| poly1d | 辅助函数polyint |
5. interpolate 模块
插值是在直线或曲线上的两点之间找到值的过程,比如在给出有限的离散数据点时,当我们想要根据数据点拟合出一条曲线,就可以利用插值的方法。 这种插值工具不仅适用于统计学,而且在科学,商业或需要预测两个现有数据点内的值时也很有用。
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(30,30))
x1 = np.linspace(-2, 2, 20)
x2 = np.linspace(-2, 2, 100)
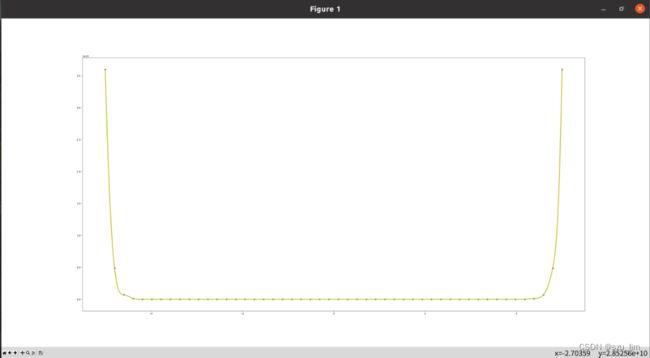
y = np.cosh(x1**2)
f1 = interpolate.interp1d(x1, y,kind = 'linear')
f2 = interpolate.interp1d(x1, y, kind = 'cubic')
plt.plot(x1,y,'o',x2,f1(x2),x2,f2(x2))
plt.show()
interp1d是一种创建基于固定数据点的函数的便捷方法,可以使用线性插值在给定数据定义的域内的任意位置评估该函数,拟合精度随着插值的数量增大而提高,这些函数对于给定的输入x返回y, 第三个参数表示插值的类型。
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
fig = plt.figure(figsize=(30,30))
x1 = np.linspace(-5, 5, 50)
x2 = np.linspace(-5, 5, 500)
y = np.sinh(x1**2) - np.random.randn(50)
spl = UnivariateSpline(x1, y)
spl.set_smoothing_factor(0.5)
plt.plot(x1, y, 'bo', ms = 5)
plt.plot(x2, spl(x2), 'y', lw = 3)
plt.show()
我们也可以画出平滑的一维曲线来拟合一组给定的数据点,interpolate模块中的UnivariateSpline类是创建基于固定数据点类的函数的便捷方法,该方法可以直接调节曲线的平滑度。
6. linalg模块
Scipy库具有很强很快的线性代数求解能力,所有这些线性代数例程都需要一个可以转换为二维数组的对象,这些例程的输出也是一个二维数组。linalg模块下的solve方法可以求解线性方程,返回的结果是变量的解的数组
from scipy import linalg
import numpy as np
# 2x+ 2y= 2
# x- y= 4
# 5y+ 5z= -1
arr1 = np.array([[2, 2, 0], [1, -1, 0], [0, 5, 5]])
arr2 = np.array([2, 4, -1])
arr3 = linalg.solve(arr1, arr2)
print (arr3)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code9.py
[ 2.5 -1.5 1.3]
#Process finished with exit code 0
行列式是线性代数中经常使用的, 在SciPy的linalg模块中,我们可以通过det方法计算行列式并返回一个标量值。
from scipy import linalg
import numpy as np
arr1 = np.array([[2, 2, 0], [1, -1, 0], [0, 5, 5]])
arr2 = np.arange(1,5).reshape(2,2)
l,v = linalg.eig(arr2)
print(linalg.det(arr1))
print('\n')
print(l)
print('\n')
print(v)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code9.py
-20.0
[-0.37228132+0.j 5.37228132+0.j]
[[-0.82456484 -0.41597356]
[ 0.56576746 -0.90937671]]
#Process finished with exit code 0
特征值和特征向量问题是最常用的线性代数运算之一,A为n阶矩阵,若数λ和n维非0列向量x满足Ax=λx,那么数λ称为A的特征值,x称为A的对应于特征值λ的特征向量, 我们可以通过linalg模块里的eig方法来计算方阵(A)的特征值(λ)和相应的特征向量(x) 。
7. ndimage模块
边缘检测是一种用于查找图像内物体边界的图像处理技术。它通过检测亮度不连续性来感知边缘,边缘检测常用于图像处理,计算机视觉和机器视觉等领域的图像分割和数据提取。
from scipy import ndimage
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(30,30))
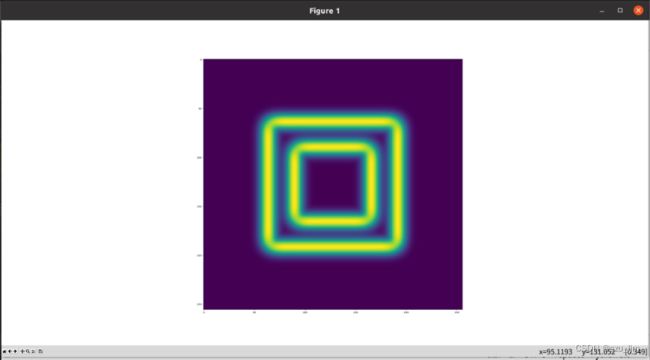
im1 = np.zeros((256, 256))
im1[64:-64, 64:-64] = 1
im1[90:-90,90:-90] = 2
im1 = ndimage.gaussian_filter(im1, 6)
sx = ndimage.sobel(im1, axis = 0, mode = 'constant')
sy = ndimage.sobel(im1, axis = 1, mode = 'constant')
im2 = np.hypot(sx, sy)
plt.imshow(im1)
plt.show()
plt.imshow(im2)
plt.show()
我们刚开始生成256*256像素点的图像,并用ndimage模块下的gaussian_filter方法来调整图像模糊度,接着使用ndimage提供的Sobel函数检测这些彩色块的边缘,NumPy提供了Hypot函数来将两个合成矩阵合并为一个。
8. optimize模块
optimize模块包含很多优化算法(这里主要介绍最小二乘和求根):
各种算法的无约束和约束最小化多元标量函数(minimize())
全局优化程序(anneal(),basinhopping())
最小二乘最小化(leastsq()) 和曲线拟合(curve_fit())
算法标量单变量函数最小化(minim_scalar())和根查找(newton())
使用多种算法的多元方程系统求解(Powell,Levenberg-Marquardt混合或Newton-Krylov等大规模方法)
最小二乘法问题的常见解法
最小二乘问题的主要思想就是求解未知参数 ,使得预测值与观测值之差(即误差,或者说残差)的平方和达到最小。 给定残差f(x)和损失函数rho(s),最小二乘法找到代价函数F(x)的局部最小值。
from scipy.optimize import least_squares
import numpy as np
def fun_rosenbrock(x):
return np.array([10 * (x[1] - x[0]**2), (1 - x[0])])
arr1 = np.array([2, 2])
result = least_squares(fun_rosenbrock, arr2)
print (result)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code9.py
message: `gtol` termination condition is satisfied.
success: True
status: 1
fun: [ 4.441e-15 1.110e-16]
x: [ 1.000e+00 1.000e+00]
cost: 9.866924291084687e-30
jac: [[-2.000e+01 1.000e+01]
[-1.000e+00 0.000e+00]]
grad: [-8.893e-14 4.441e-14]
optimality: 8.892886493421953e-14
active_mask: [ 0.000e+00 0.000e+00]
nfev: 3
njev: 3
#Process finished with exit code 0
遇到一个单变量超越方程,则可以尝试brentq函数,它可以在给定区域内查找函数的根。在求解一组超越方程的根时,我们可以借助optimize模块的root函数,它可以求解一组非线性方程的根。
import numpy as np
from scipy.optimize import brentq
def func(x):
return np.exp(x) + np.cos(x)
result = brentq(func, -4, 4)
print (result)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code9.py
-1.7461395304080782
#Process finished with exit code 0
9. stats模块
scipy中stats模块包含大量的概率分布以及统计函数库,并且可以使用info(stats)函数获得这些函数的完整列表,随机变量列表也可以从stats模块的docstring中获得。
每个单变量分布都有其自己的子类,rv_continuous指向通用连续随机变量类,rv_discrete指向通用离散随机变量类。
cdf是机器学习里的累计分布函数,它表示在x点左侧事件发生的总和,cdf的导数就是概率密度函数,用于反应事件发生的概率分布。下面我们用正态分布来生成样本数据,位置(loc)关键字指定平均值,比例(scale)关键字指定标准偏差
from scipy.stats import norm
import numpy as np
arr1 = norm.cdf(np.array([0,1,2,3,4,5]))
mid_number = norm.ppf(0.5)
print(arr1)
print('\n')
print(mid_number)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code9.py
[0.5 0.84134475 0.97724987 0.9986501 0.99996833 0.99999971]
0.0
#Process finished with exit code 0
ppf方法可用于求数据样本的中位数,二项分布的样本数据作为rv_discrete类的一个实例,binom对象从它继承了一个泛型方法的集合,并通过特定于这个特定分布的细节完成它们
from scipy.stats import uniform
arr1 = uniform.cdf([0, 1, 2, 3, 4, 5], loc = 2.5, scale = 0.5)
print(arr1)
#/usr/bin/python3.8 /home/ljm/PycharmProject/pythoncode1/code9.py
[0. 0. 0. 1. 1. 1.]
#Process finished with exit code 0
下面是描述型统计的一些常用函数
| 函数 | 描述 |
|---|---|
| describe() | 计算传递数组的几个描述性统计信息 |
| gmean() | 计算沿指定轴的几何平均值 |
| hmean() | 计算沿指定轴的谐波平均值 |
| kurtosis() | 计算峰度 |
| mode() | 返回模态值 |
| skew() | 测试数据的偏斜度 |
| f_oneway() | 执行单向方差分析 |
| iqr() | 计算沿指定轴的数据的四分位数范围 |
| zscore() | 计算样本中每个值相对于样本均值和标准偏差的z值 |
| sem() | 计算输入数组中值的标准误差(或测量标准误差) |
10. ord模块
ODR代表正交距离回归,用于解决线性回归问题, 基本线性回归通常用于通过在图上绘制最佳拟合线来估计两个变量y和x之间的关系。正交方法能够同时考虑自变量x 和因变量y的误差。
正交回归将横纵坐标残差的平方和作为目标函数,来求得最优解。直观地理解,正交回归就是找到一条直线,使得点到直线的距离之和最小。所以如果拟合点的横纵坐标都包含误差的情况下,使用正交回归能够得到比最小二乘法更准确的结果。
import numpy as np
import matplotlib.pyplot as plt
from scipy.odr import *
import random
# Initiate some data, giving some randomness using random.random().
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([i**2 + random.random() for i in x])
# Define a function (quadratic in our case) to fit the data with.
def linear_func(p, x):
m, c = p
return m*x + c
# Create a model for fitting.
linear_model = Model(linear_func)
# Create a RealData object using our initiated data from above.
data = RealData(x, y)
# Set up ODR with the model and data.
odr = ODR(data, linear_model, beta0=[0., 1.])
# Run the regression.
out = odr.run()
# Use the in-built pprint method to give us results.
out.pprint()
#Beta: [ 5.50355382 -3.88825011]
#Beta Std Error: [ 0.77904626 2.33231797]
#Beta Covariance: [[ 1.92223609 -4.80559051][ -4.80559051 17.22882877]]
#Residual Variance: 0.31573284521355344
#Inverse Condition #: 0.1465848083469268
#Reason(s) for Halting:
# Sum of squares convergence
总结
以上就是今天scipy库简单入门的内容,这次笔记仅仅简单介绍了scipy一部分工具的使用,scipy中还有大量的数据科学工具等待我们学习使用。由于作者能力有限,对机器学习的了解也是刚刚入门,scipy库也是机器学习的冰山一角,愿热爱机器学习的小伙伴都能在学习探索这片天地中收获自己的快乐,最后提前祝各位小伙伴新年快乐!!!