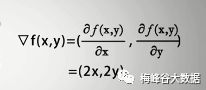【AI】梯度下降的数学原理(05)

目录

1、导数的概念

2、导数的求法

3、求导的几何意义

4、多元函数及偏导

5、梯度的概念和计算方法

5.1 梯度的概念

5.2 梯度的计算方法

5.3 梯度方向，函数值变化最迅猛的原因

---

1、导数的概念

导数：一个函数在某一点导数，描述了这个函数在这个点的变化率

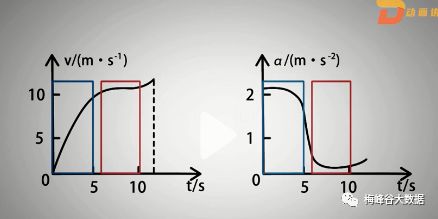
例子1：运动员的速度和时间t的变化曲线：我们想得到速度变化的快慢，那就需要得到加速度a和时间变化的曲线，速度变化越快，加速度就越大，如蓝色方框这个，速度变化越小，那加速度变化就越小，如下红色方框。

我们可以看到，1）起跑的时候，加速度非常快，2）随后，加速度变小，3）最后冲刺，加速度变大。这里的加速度表示的是速度变化快慢，公式求法，就是求导

这里的加速度，就是速度在曲线上的变化率，下面的红色条线就是斜率

2、导数的求法

导数的求法有很多公式，如幂函数等等，都比较实用

举例

多项式求导，对每一项都要求导

3、求导的几何意义

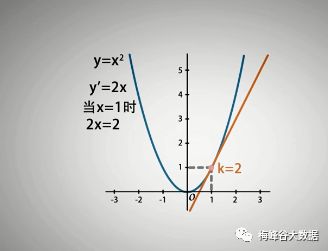
   比如 y= x的平方，几何图形如下，他的导数 y'=2x，当x=1时，导数值k=2，几何意义表示:在x=2时，曲线的斜率。

4、多元函数及偏导

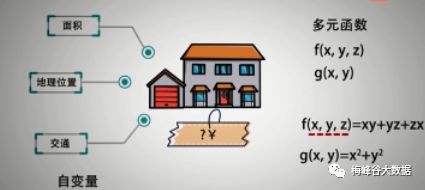
函数不可能只有一个影响因子，可能会有多个因子，当有多个因子的时候，就用多元函数来表示，比如房屋的价格，就会受到多种因子影响

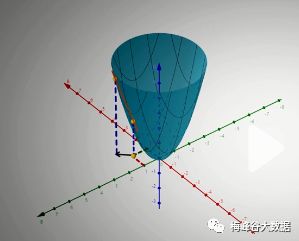
几何图像举例，多元函数中的x，y也都有一个z和他对应，是一个曲面，这个多元函数应如何求导呢

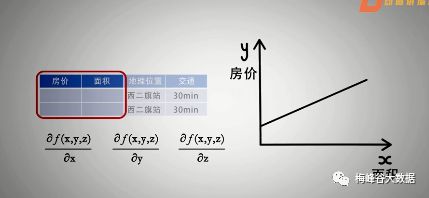
多元函数的导数就要用偏导来求，单个变量因子的导数是关于自变量的变化率，多元函数就是关于多个自变量的变化率了，多元函数中求某个变量的导数的时候，其他的就看做是常数。

举例如下，仅对x或者仅对y求导

5、梯度的概念和计算方法

5.1 梯度的概念

梯度概念：函数在某一点出沿着不同的方向运动，函数值的变化率是不同的，梯度可以定义为一个函数的全部偏导数构成的向量。梯度向量的方向是函数值变化率最大的方向。也就是对函数的某个特定点，函数值变化最迅猛的地方。

使用拉姆达做来表示某个函数的梯度，二元函数f(x,y),梯度是对x,y求偏导组成的二维向量。

三元函数g(x,y,z)的梯度是对x,y，z求偏导组成的三维向量

n元函数的梯度就是分别对n个自变量求偏导构成的n维向量

5.2 梯度的计算方法

举个具体的例子f(x,y) = x的平方+y的平方，他们的梯度就是（2x,2y）

那么在点（1,1）处的梯度向量为（2,2），在点（1,1）处沿该向量变化，函数值变化最快

5.3 梯度方向，函数值变化最迅猛的原因

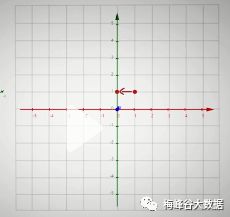
为了方便观察，画出xOy平面，在点（1,1）的位置，我们分步骤来说明为什么沿着梯度方向是移动最迅猛的

f(x)= x的平方+y的平方，

在点（1，1）处

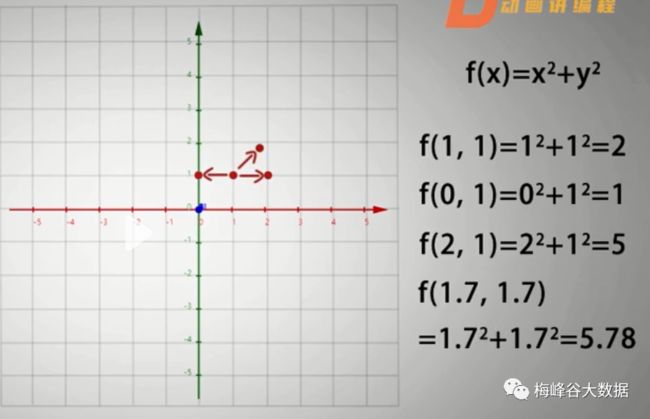
第一步：计算在点（1,1）时的函数值，值为f(1,1) = 1的平方+1的平方 = 2 

第二步：如果按照向量（-1，0） 的方向移动，就是就移动一个单位，移动后的点为（0,1），函数值为1，比f(1,1)减少了1 

第三步：如果按照向量（1,0）的方向移动，到达（2,1），函数值为5，比f（1,1）增加了3

第四步，按照梯度方向(2,2)移动1，大约到达（1.7,1.7）,函数值为5.78，增加了3.78，所以按照梯度方向移动，函数值增长的最迅猛

综上，通过三个不同方向的函数值的移动后变化对比，方向按照梯度方向的变化是最迅猛的。

本偏博文来自抖音号《动画讲编程》，特别鸣谢，更多AI文章请关注VX公众号